Математическая модель на основе метода молекулярной динамики описывает перенос вещества в порах диаметром от 1 до 1000 нм, длиной от 0,01 до 200 мкм, при давлениях от 0,001 до 2 атм. При малых размерах пор перенос вещества [1] происходит как за счет столкновения молекул друг с другом (молекулярная диффузия), так и за счет соударений молекул со стенкой поры (диффузия Кнудсена), причем второй тип преобладает, так как вероятность соударения молекул друг с другом при низком давлении довольно мала. После задания начальных условий (длина, диаметр поры, температура, давление, молекулярная масса газа) производится расчет количества молекул в поре в соответствии с законом Менделеева–Клапейрона 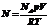 , где NA – число Авогадро; V – объем поры.
, где NA – число Авогадро; V – объем поры.
Средняя скорость молекул газа рассчитывается из распределения Максвелла–Больцмана. После вычисления средней скорости молекул газа каждой молекуле присваивается определенная скорость с учетом вероятности из распределения Максвелла.
Взаимодействие молекул описывается с применением межмолекулярного потенциала взаимодействия Леннарда–Джонса
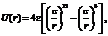
где r – расстояние между центрами частиц; e – глубина потенциальной ямы; s – расстояние, на котором энергия взаимодействия становится равной нулю. Параметры e и s являются характеристиками молекул соответствующего вещества.
С использованием генератора случайных чисел и с учетом распределения давления по поре всем частицам (молекулам) присваиваются начальные координаты их местоположения. Далее координаты положения частиц меняются в соответствии с уравнениями движения.
При столкновении со стенкой пересчитываются скорости с учетом зеркального и диффузного механизмов рассеяния. При зеркальном рассеянии частиц происходит абсолютно упругий удар, и частица отлетает от стенки под тем же углом, под которым она приближалась к ней. При диффузном рассеянии новое направление движения частицы определяется с помощью генератора случайных чисел. В обоих случаях модуль вектора скорости остается постоянным. Проверка частиц на столкновение проводится только для наиболее близко расположенных друг к другу частиц, для которых возникает наибольшая вероятность соударения.
Организация параллельных вычислений осуществляется с применением технологии CUDA. Преимущество использования технологии параллельного программирования в том, что при моделировании необходимо проводить множество однотипных операций над всеми частицами (проверка на столкновения, численное решение уравнений движения и др.). Для такой задачи хорошо подходят решения на основе принципа SIMD (single instruction-stream, multiple data-stream – один поток команд с несколькими потоками данных), когда вычислительное устройство выполняет операции сразу над несколькими элементами данных за один такт [2]. На этом принципе построена и используемая в данной реализации технология CUDA.
Для хранения параметров частиц используется трехмерный массив. Число ячеек массива соответствует числу частиц в системе. В каждой ячейке массива хранятся параметры какой-либо частицы: координаты, вектор скорости, вектор ускорения и тип. Отдельно существует одномерный массив типов. Количество элементов массива равно количеству типов частиц, присутствующих в системе. В ячейках хранятся параметры каждого из веществ, имеющихся в системе, – масса и радиус частицы, коэффициенты потенциала межмолекулярного взаимодействия. В ходе расчета при необходимости получения доступа к этим параметрам они берутся из ячейки с номером, соответствующим типу рассчитываемой частицы.
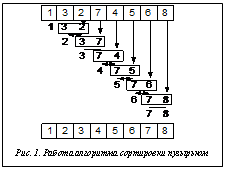 Алгоритм для сортировки частиц требует упорядоченности массива по координатам частиц. Для упорядочения элементов применяется простой алгоритм сортировки пузырьком [3], приспособленный для параллельной реализации, и расширенный – для трехмерного случая. Пусть имеется одномерный неупорядоченный массив a из n элементов. Алгоритм состоит в повторяющихся проходах по сортируемому массиву. За каждый проход элементы последовательно сравниваются попарно и, если порядок в паре неверный, выполняется их обмен (рис. 1). Проходы по массиву повторяются до тех пор, пока не окажется, что обмены больше не нужны, это означает, что массив отсортирован.
Алгоритм для сортировки частиц требует упорядоченности массива по координатам частиц. Для упорядочения элементов применяется простой алгоритм сортировки пузырьком [3], приспособленный для параллельной реализации, и расширенный – для трехмерного случая. Пусть имеется одномерный неупорядоченный массив a из n элементов. Алгоритм состоит в повторяющихся проходах по сортируемому массиву. За каждый проход элементы последовательно сравниваются попарно и, если порядок в паре неверный, выполняется их обмен (рис. 1). Проходы по массиву повторяются до тех пор, пока не окажется, что обмены больше не нужны, это означает, что массив отсортирован.
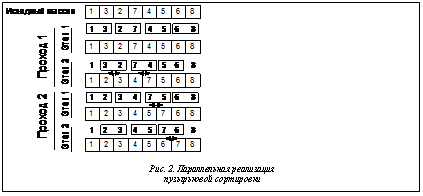
При параллельной реализации каждый проход по массиву разделяется на 2 этапа. На первом попарно сравниваются элементы с номерами 2i и 2i+1 (нулевой с первым, второй с третьим и т.д.). На втором этапе происходит то же самое, но со сдвигом на 1 позицию, то есть сравниваются 2i+1 и 2i+2 элементы (рис. 2).
 В результате после прохода массив становится частично отсортированным, как и в оригинальном алгоритме, однако в пределах одного этапа все сравнения могут выполняться параллельно. Понадобится n/2 потоков, каждый из них обработает одну пару элементов. Так как не будет происходить перекрывание данных, алгоритм не требует блокировок и все потоки могут выполняться одновременно.
В результате после прохода массив становится частично отсортированным, как и в оригинальном алгоритме, однако в пределах одного этапа все сравнения могут выполняться параллельно. Понадобится n/2 потоков, каждый из них обработает одну пару элементов. Так как не будет происходить перекрывание данных, алгоритм не требует блокировок и все потоки могут выполняться одновременно.
Рассмотрим трехмерный массив с размерностью L´M´N. Причем, в отличие от одномерного случая, когда в ячейках массива хранилось всего одно число, в трехмерном случае каждая ячейка будет представлять собой вектор из трех координат (x, y, z). Шаг сортировки для такого массива с применением вышеописанного одномерного алгоритма выбирается следующим образом. Очевидно, что трехмерный массив L´M´N можно представить в виде N´M одномерных массивов из L элементов. Для каждого из этих массивов следует выполнить проход алгоритма сортировки, причем для сравнения значения x брать из ячеек. После этого трехмерный массив будет частично отсортирован по одной из размерностей. Аналогично следует выполнить проход по двум другим размерностям, сравнивая соответствующие координаты, то есть для M-массивов берутся координаты y, а для N-массивов – координаты z. В итоге после такого прохода массив будет частично отсортирован по всем трем координатам.
В общем случае для полной сортировки массива проходы должны выполняться до тех пор, пока не прекратятся перестановки элементов, и для изначально неупорядоченного массива таких проходов может быть довольно много. Однако для массивов, в которых значения уже частично упорядочены, особенно для таких, которые образованы несколькими перестановками элементов упорядоченной последовательности, алгоритм показывает хорошую производительность, так как количество проходов в таких случаях довольно мало.
Массив частиц следует сортировать после каждого расчета нового положения частиц в пространстве. При таком использовании алгоритма сортировки расположение частиц в ячейках массива будет приближенно соответствовать их положению в пространстве внутри поры в процессе моделирования, что является важным условием для корректного расчета взаимодействия частиц.
 Проверка на столкновение выполняется только для тех частиц в системе, которые наиболее близко расположены друг к другу, и у них, соответственно, будет наибольшая вероятность соударения. Проверка частиц на соударение проводится в два этапа. На первом этапе массив разбивается на кубические блоки размером P´P´P (рис. 3). В каждом из этих блоков происходит полный перебор всех сочетаний из двух частиц, и для каждого выполняется проверка на соударение с последующим пересчетом скоростей при положительном результате проверки.
Проверка на столкновение выполняется только для тех частиц в системе, которые наиболее близко расположены друг к другу, и у них, соответственно, будет наибольшая вероятность соударения. Проверка частиц на соударение проводится в два этапа. На первом этапе массив разбивается на кубические блоки размером P´P´P (рис. 3). В каждом из этих блоков происходит полный перебор всех сочетаний из двух частиц, и для каждого выполняется проверка на соударение с последующим пересчетом скоростей при положительном результате проверки.
Второй этап аналогичен первому, но разбивка на блоки происходит со сдвигом, чтобы учесть столкновения, которые могли бы произойти между частицами, находящимися рядом, но попавшими на первом этапе в разные блоки. Сдвиг идет по всем трем размерностям массива на P/2 позиций.
Для организации проверки частиц на соударение со стенкой для каждой частицы в массиве проверяется, выходят ли ее координаты за пределы поры. При положительном результате скорости частицы пересчитываются. При соударении, помимо пересчета скорости, сам факт регистрируется счетчиком соударений. Регистрируются длина свободного пробега частицы от последнего соударения и время, которое прошло с последнего соударения, после чего данные о времени и длине пробега обнуляются. Эти данные необходимы для расчета коэффициента диффузии D частиц в поре. Коэффициент диффузии рассчитывается по формуле 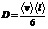 , где ávñ – средняя скорость частиц в системе; álñ – средняя длина свободного пробега.
, где ávñ – средняя скорость частиц в системе; álñ – средняя длина свободного пробега.
 С целью проверки частиц на выход из поры и организации входа частиц в пору для каждой частицы в массиве проверяется, не превышает ли координата x частицы длину поры l. Если превышение есть, частица считается вылетевшей. Факт выхода из поры регистрируется счетчиком, а ячейка, которую заполняла вылетевшая частица, заполняется новой частицей. Ей присваиваются тип в соответствии с составом, координаты и скорости, как и при начальном заполнении, за исключением того, что координаты x, у новой частицы равны 0, так как частица находится на входе в пору.
С целью проверки частиц на выход из поры и организации входа частиц в пору для каждой частицы в массиве проверяется, не превышает ли координата x частицы длину поры l. Если превышение есть, частица считается вылетевшей. Факт выхода из поры регистрируется счетчиком, а ячейка, которую заполняла вылетевшая частица, заполняется новой частицей. Ей присваиваются тип в соответствии с составом, координаты и скорости, как и при начальном заполнении, за исключением того, что координаты x, у новой частицы равны 0, так как частица находится на входе в пору.
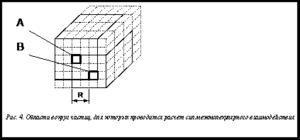
Сила межмолекулярного взаимодействия рассчитывается только для близко расположенных друг к другу частиц. Так как расположение частиц в ячейках отсортированного массива примерно соответствует их положению в пространстве, для каждой ячейки массива в соседних ячейках, вероятнее всего, будут находиться частицы, наиболее близкие к частице в данной ячейке в пространстве поры. Для расчета сил межмолекулярного взаимодействия для каждой частицы в массиве берется совокупность соседей, находящихся в ячейках не более чем в R позициях от данной (рис. 4). Из рисунка 4 видно, что области частиц A и B перекрываются, при этом каждая из частиц попадает в область другой.
 Рассчитывается только модуль силы, действующий на частицу в данной ячейке; для всех остальных ячеек выполняется такой же расчет в своей окрестности. Так как окрестности близко расположенных частиц перекрываются, для всех подобных пар будет корректно рассчитана сила парного взаимодействия (каждая из частиц рассчитает свою силу).
Рассчитывается только модуль силы, действующий на частицу в данной ячейке; для всех остальных ячеек выполняется такой же расчет в своей окрестности. Так как окрестности близко расположенных частиц перекрываются, для всех подобных пар будет корректно рассчитана сила парного взаимодействия (каждая из частиц рассчитает свою силу).
 Выходные статистические данные можно получить непосредственно (значения счетчиков соударений, счетчиков вышедших частиц), посчитав среднее арифметическое значение нужной величины для всех частиц в массиве (средняя скорость, средняя длина свободного пробега), а также вычислить по формуле (коэффициент диффузии).
Выходные статистические данные можно получить непосредственно (значения счетчиков соударений, счетчиков вышедших частиц), посчитав среднее арифметическое значение нужной величины для всех частиц в массиве (средняя скорость, средняя длина свободного пробега), а также вычислить по формуле (коэффициент диффузии).
Все данные выводятся в удобной для пользователя форме на экран монитора или на запоминающее устройство.
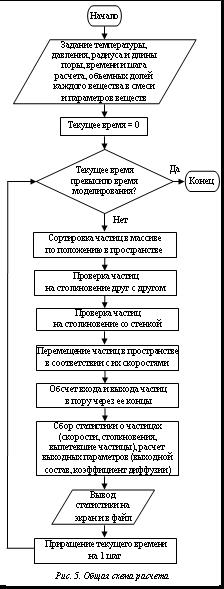
Общий алгоритм расчета осуществляется следующим образом. После ввода пользователем параметров моделирования происходят определение размера массива (из уравнения Менделеева–Клайперона) и начальное заполнение массива частицами. Частицам присваиваются тип в соответствии с заданным составом смеси (так как состав задается мольными долями, которые могут быть пересчитаны непосредственно в количество молекул, в итоге количество частиц разных типов в массиве отражает состав смеси), начальные пространственные координаты, начальные скорости (в соответствии с распределением Максвелла). Задаются шаг моделирования по времени и общее время моделирования, текущее время моделирования устанавливается на 0. После этого запускается процесс моделирования массопереноса в поре, который состоит в выполнении над массивом частиц повторяющейся последовательности операций (рис. 5):
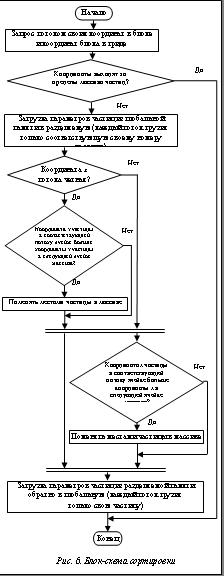
– частичная сортировка массива одним проходом сортировки (рис. 6), в результате которой будут пересчитаны скорости для столкнувшихся частиц;
– фактическое выполнение моделирования (если проверка частиц на столкновение друг с другом не проводится) с учетом только кнудсеновской диффузии, так как частицы не взаимодействуют друг с другом;
– проверка частиц на столкновение со стенкой, в результате которой будут пересчитаны скорости столкнувшихся со стенкой частиц;
– расчет сил межмолекулярного взаимодействия, в результате которого всем частицам будут приданы соответствующие ускорения; если расчет не проводится, моделирование проходит без учета сил межмолекулярного взаимодействия;
– проверка частиц на выход из поры и организация входа частиц в пору;
– расчет нового положения частиц в соответствии с уравнениями движения, в результате чего частицам будет присвоено новое положение в пространстве;
– сбор статистики для определения выходных данных моделирования;
– увеличение текущего времени моделирования на величину шага и проверка, не превысило ли оно заданное время моделирования; при отрицательном результате повторение последовательности (то есть новый шаг по времени), при положительном расчет заканчивается.
Применение технологии организации параллельного вычисления CUDA для описания математической модели позволяет существенно быстрее производить расчеты для большого количества молекул N, которое в зависимости от условий (давление, температура, длина, диаметр поры) может варьироваться от 1 до 100 тыс. молекул по сравнению с однопоточной версией программы.
Литература
1. Albo S.E., Broadbelt L.J., Snurr R.Q. // AIChE Journal, 2006, Vol. 52, no. 11, pp. 3679–3687.
2. Таненбаум Э. Архитектура компьютера. СПб: Питер, 2007. 5-е изд. 844 c.
3. Левитин А.В. Алгоритмы: введение в разработку и анализ. М.: Изд-во «Вильямс», 2006. 576 с.



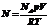 , где NA – число Авогадро; V – объем поры.
, где NA – число Авогадро; V – объем поры.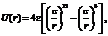
 Алгоритм для сортировки частиц требует упорядоченности массива по координатам частиц. Для упорядочения элементов применяется простой алгоритм сортировки пузырьком [3], приспособленный для параллельной реализации, и расширенный – для трехмерного случая. Пусть имеется одномерный неупорядоченный массив a из n элементов. Алгоритм состоит в повторяющихся проходах по сортируемому массиву. За каждый проход элементы последовательно сравниваются попарно и, если порядок в паре неверный, выполняется их обмен (рис. 1). Проходы по массиву повторяются до тех пор, пока не окажется, что обмены больше не нужны, это означает, что массив отсортирован.
Алгоритм для сортировки частиц требует упорядоченности массива по координатам частиц. Для упорядочения элементов применяется простой алгоритм сортировки пузырьком [3], приспособленный для параллельной реализации, и расширенный – для трехмерного случая. Пусть имеется одномерный неупорядоченный массив a из n элементов. Алгоритм состоит в повторяющихся проходах по сортируемому массиву. За каждый проход элементы последовательно сравниваются попарно и, если порядок в паре неверный, выполняется их обмен (рис. 1). Проходы по массиву повторяются до тех пор, пока не окажется, что обмены больше не нужны, это означает, что массив отсортирован. В результате после прохода массив становится частично отсортированным, как и в оригинальном алгоритме, однако в пределах одного этапа все сравнения могут выполняться параллельно. Понадобится n/2 потоков, каждый из них обработает одну пару элементов. Так как не будет происходить перекрывание данных, алгоритм не требует блокировок и все потоки могут выполняться одновременно.
В результате после прохода массив становится частично отсортированным, как и в оригинальном алгоритме, однако в пределах одного этапа все сравнения могут выполняться параллельно. Понадобится n/2 потоков, каждый из них обработает одну пару элементов. Так как не будет происходить перекрывание данных, алгоритм не требует блокировок и все потоки могут выполняться одновременно.
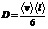 , где ávñ – средняя скорость частиц в системе; álñ – средняя длина свободного пробега.
, где ávñ – средняя скорость частиц в системе; álñ – средняя длина свободного пробега.


