Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Алгоритм сравнения методов комплексной количественной оценки качества сложных систем
Аннотация:Описывается применение различных методов комплексной количественной оценки качества сложных систем для сравнения и выбора наилучшего варианта из альтернативных. Рассматривается наличие неопределенности в выборе метода, существенно затрудняющей получение объективной оценки качества сложных систем, что влияет на обоснованность решений, принимаемых при их выборе. Предлагается решение данной проблемы, которое позволяет разрешить неопределенность в выборе метода, сняв противоречивость между результатами решений различными методами. Приводится алгоритм, суть которого состоит в определении рационального метода из возможной совокупности методов. Применение данного алгоритма минимизирует риск получения неверного решения вследствие выбора нерационального метода из возможной совокупности методов количественной оценки качества сложных систем. Кроме того, в статье приведены результаты экспериментов на реальных сложных системах, подтверждающие эффективность применения разработанного алгоритма для сравнения методов сверток, введения метрик и экспертных оценок при сравнении, оценке и выборе сложных систем.
Abstract:This work considers the application of various methods of complex quantitative quality evaluation of compound systems to compare and choose the best version of the alternative. As well as the availability of uncertainly in the choice of a method which makes it difficult to obtain an objective assessment of the quality of complex systems, which affects on the validity of the decisions taken in their selection. Offer a solution to this problem, which allows the uncertainly in the choice of a method, removing the inconsistency between the results of different methods of solutions. The algorithm, the essence of which is to define a rational method of the possible combination of methods. An algorithm that minimizes the risk of wrong decisions due to the irrational choice of the method of the possible set of methods for quantitative evaluation of quality systems. Experimental results on real complex systems, confirming the effectiveness of the developed algorithm for comparing the methods package, introducing metrics and expertise in the comparison, evaluation and selection of complex systems are given.
| Авторы: Лисецкий Ю.М. (Iurii.Lisetskyi@snt.ua) - Компания «ЭС ЭНД ТИ УКРАИНА» (генеральный директор), г. Киев, Украина, кандидат технических наук | |
| Ключевые слова: отношение упорядочений., минимизация риска, рациональный метод, сравнение и выбор, сложная система, алгоритм |
|
| Keywords: the ratio of regulations, risk minimization, efficient method, comparison and selection, complex system, algorithm |
|
| Количество просмотров: 10912 |
Версия для печати Выпуск в формате PDF (9.63Мб) Скачать обложку в формате PDF (1.26Мб) |
При решении задачи оценки, сравнения и выбора сложных систем (далее систем) в большинстве случаев используются методы, основанные на свертках, введении метрик и экспертных оценках [1–3]. Как показывают проведенная классификация и анализ [4], области применения этих методов пересекаются, то есть несколько методов могут использоваться для решения одной и той же задачи, что обусловливает неопределенность в выборе метода. Наличие такой неопределенности существенно затрудняет получение объективной оценки качества систем. Это влияет на обоснованность решений, принимаемых при их выборе. Для устранения данной проблемы необходимо разрешить неопределенность в выборе метода из всей возможной совокупности, сняв противоречия между результатами решений разными методами. Для сравнения оценок, получаемых различными методами комплексной количественной оценки качества систем, был разработан специальный алгоритм. Описание алгоритма Исходными данными для алгоритма стали варианты реализации реальной сложной системы, представленные в виде матрицы системы-характеристики. Было выполнено пропорциональное нормирование характеристик. Затем с помощью различных методов количественной оценки, в том числе и метода итерационного выбора систем (МИВС), разработанного автором [5], получены различные результаты упорядочения систем. В качестве показателя, отражающего расхождение оценок, полученных различными методами, предложено использовать отношение числа неодинаковых упорядочений к общему числу упорядочений. Результатом попарного сравнения является матрица расхождений результатов упорядочения альтернативных вариантов систем различными методами, по которой рассчитывается среднее расхождение результатов между методами. Рациональным считается метод, который в среднем имеет меньшее количество изменений упорядочения вариантов системы.
В состав схемы алгоритма входят двенадцать блоков. Блок 1 – ввод и корректировка описаний исследуемых систем, представленных в виде вектора характеристик Xi= (x1=x2, …, xn). Блок 2 – приведение характеристик исследуемых систем {K} к единой размерности с помощью пропорционального нормирования: 0 для
1 для Блок 3 – инициализация начала цикла по просмотру методов комплексной количественной оценки качества систем. Блок 4 – реализация методов оценки качества вариантов систем путем выбора i-го метода из совокупности, представленной в таблице. Результатом работы является матрица оценок Ao:
Блок 5 – проверка, все ли методы использованы; в случае реализации всех методов разрешается переход к блоку 7. Блок 6 – переход к следующему методу в случае получения оценки качества систем не всеми методами. Блоки 7 и 10 – выделение очередной пары методов для сравнения результатов оценки систем. Блок 8 – сравнение результатов упорядочения каждой пары методов и вычисление расхождения их результатов по оценке качества систем как отношение числа неодинаковых упорядочений к общему числу упорядочений, занесение результата сравнения в матрицу расхождений Ar:
Блок 9 – проверка, все ли пары методов использованы; в случае попарного сравнения результатов упорядочения всех методов переход к блоку 11. Блок 11 – расчет среднего расхождения оценок по результатам оценок каждым из методов:
Блок 12 – преобразование результатов расчета расхождений в удобный для восприятия вид. Минимальное расхождение результатов упорядочения между методами соответствует минимальному среднему риску принятия нерационального решения. Экспериментальные результаты Для проведения экспериментов настоящий алгоритм был программно реализован на языке С++. С помощью данной программной реализации проводились практические исследования, сравнения результатов решения задачи упорядочения различными методами комплексной количественной оценки качества систем, в том числе и МИВС. Всего было проведено 480 вычислительных экспериментов для различных по содержанию и формальным свойствам исходных данных. По результатам каждого эксперимента определялось количество рациональных решений – n, где n£N, каждым из i методов. Затем рассчитывалась оценка вероятности нахождения рационального решения i-м методом:
где N – количество экспериментов. По результатам всех вычислительных экспериментов определялся метод, показавший максимальную оценку вероятности нахождения рационального решения. Сравнивая результаты решения задачи упорядочения этим методом с результатами, полученными с помощью МИВС, находилась оценка вероятности уменьшения риска выбора нерационального варианта:
где maxPi – максимальная оценка вероятности нахождения рационального решения i-м методом; PМИВС – оценка вероятности нахождения рационального решения МИВС. Обобщенные результаты всех экспериментов, представляющие собой средний риск принятия нерационального решения по каждому из методов, приведены в таблице.
Анализ результатов, приведенных в таблице, позволяет сделать вывод, что в 96 % случаев оценка, полученная с помощью МИВС, является наилучшей:
В итоге вероятность выбора нерационального решения снижается в среднем на 29 %:
что экспериментально подтверждает положение о минимизации риска принятия нерационального решения при выборе сложных систем с помощью МИВС. Представленный алгоритм сравнения методов комплексной количественной оценки качества систем, суть которого в определении рационального метода из их возможной совокупности, достаточно легко реализуется программно. Сложность выбора рационального метода обусловлена тем, что для любой реальной системы такой метод, как правило, неизвестен. О рациональности какого-либо метода для анализа исследуемой системы можно говорить лишь с той или иной степенью достоверности. Предложенный способ сравнения методов минимизирует риск получения неверного решения вследствие выбора нерационального метода количественной оценки качества систем из группы методов. Это особенно актуально в задачах оценки, сравнения и выбора сложных систем. Пакет прикладных программ успешно прошел опытную апробацию. Реализованные в нем функциональные возможности использовались для решения задач сравнения и выбора при построении корпоративных интегрированных информационных систем различной степени сложности. На основании проведенных вычислительных экспериментов следует сделать вывод о том, что разработанный пакет программ может использоваться для эффективного решения широкого круга прикладных задач, где необходимо применять математический аппарат, основанный на методах сверток, введении метрик и экспертных оценках. Литература 1. Шор Я.Б. Методы комплексной оценки качества продукции. М.: Знание, 1971. 54 с. 2. Калниболотский Ю.М., Сундучков К.С., Солодовник А.И. Автоматизированное проектирование электронных схем. К.: Техника, 1987. 301 с. 3. Бешелев С.Д., Гурвич Ф.Г. Математико-статистические методы экспертных оценок. М.: Статистика, 1980. 263 с. 4. Лисецкий Ю.М. Метод комплексной экспертной оценки для проектирования сложных технических систем // Математические машины и системы. 2006. № 2. С. 141–146. 5. Лисецкий Ю.М. Выбор сложных систем по критерию минимума среднего риска // Управляющие системы и машины. 2007. № 3. С. 22–25. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=3331 |
Версия для печати Выпуск в формате PDF (9.63Мб) Скачать обложку в формате PDF (1.26Мб) |
| Статья опубликована в выпуске журнала № 4 за 2012 год. [ на стр. 153-156 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Комплекс программ идентификации точечных дефектов листового стекла
- Программное обеспечение навыковой системы принятия решений
- Способы реализации алгоритмов интегральных преобразований изображений по линиям
- Рекурсивный алгоритм точного расчета ранговых критериев проверки статистических гипотез
- Разработка алгоритмов функционирования математической модели дирижабельного радиолокационного комплекса обнаружения малозаметных воздушных целей
Назад, к списку статей



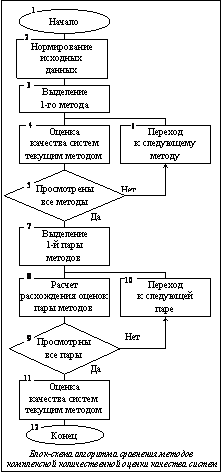 Блок-схема алгоритма, реализующего данное сравнение, представлена на рисунке.
Блок-схема алгоритма, реализующего данное сравнение, представлена на рисунке.
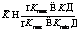 для
для 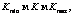 (1)
(1)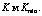
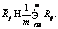 (2)
(2)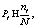 (3)
(3)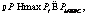 (4)
(4)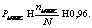 (5)
(5)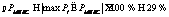 , (6)
, (6)