Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Оптимизация процессов в сверхкритическом реакторе
Аннотация:Computational Fluid Dynamics (CFD) моделирование – мощный численный метод решения уравнений, связанных с течением жидкостей и газов. За последние десять лет CFD-моделирование стало неотъемлемой частью инженерного дизайна и анализа многих компаний благодаря возможности предсказывать поведение новых схем и процессов до того, как они будут реализованы и использованы. CFD-пакеты сейчас рассматриваются как стандартный инструмент не только для предсказания поведения жидкости, но и для описания переноса тепла, массы (например растворение), фазовых переходов (заморозка, таяние, кипение), химических превращений (горение, окисление), механического движения (мешалки, турбины и т.д.) и деформации твердых конструкций. Развитие новых направлений промышленности требует проектирования нового оборудования и разработки новых технологических схем, удовлетворяющих требованию выпуска качественного материала с учетом ресурсо- и энергосбережения, а также экологических проблем. Сверхкритическая сушка является единственным методом получения такого нанопористого материала, как аэрогель. По своей сути сверхкритическая сушка – это процесс диффузионного замещения растворителя в порах геля на сверхкритический флюид с последующим сбросом давления до атмосферного и, следовательно, с переводом флюида в газообразное состояние. Данный процесс обычно ведется при давлении 80–180 атм и температуре не меньше 31°С. Для его реализации необходим специальный реактор, рассчитанный на такие параметры и изготовленный из соответствующих материалов. В статье представлен пример использования программного пакета CFD Fluent для решения задачи оптимизации процесса сверхкритической сушки в реакторе определенной геометрии. Показана наилучшая геометрия изучаемого объекта, а также даны рекомендации по его модернизации.
Abstract:Computational Fluid Dynamics (CFD) modeling is a powerful numerical method for solving equations related to the flow of liquids and gases. Over the last ten years, CFD modeling has become an integral part of engineer design and analyses of many companies due to its ability to predict new schemes and processes before their realization and application. Nowadays, CFD software packages are considered as a standard tool not only for prediction of the liquid’s behavior, but also for description of heat transfer, mass transfer (dissolution), phase transition (freezing, melting, boiling), chemical transformation (combustion, oxidation), mechanical motion (agitator, turbine) and deformation of solid constructions. Development of new areas of industry requires design of new equipment and technological schemes that respond to the requirement of production of qualitative material, considering resource and energy conservation and taking into account ecology problems. Supercritical drying is a method of aerogel obtainment. At its core, the supercritical drying is a solvent replacement in the pores of the gel on the supercritical fluid by diffusion. After that, pressure reset to the atmospheric and, therefore, fluid transfer in the gaseous state. Special reactor is needed to implement such a process. It must be designed for the required parameters and manufactured with appropriate materials. The article presents an example of using CFD Fluent software package for processes optimization in supercritical reactor of certain geometry. The best geometry of the object was shown and recommendations for modernization were done.
| Авторы: Меньшутина Н.В. (chemcom@muctr.ru) - Российский химико-технологический университет им. Д.И. Менделеева (профессор), г. Москва, Россия, доктор технических наук, Каталевич А.М. (patlaten@yandex.ru) - Российский химико-технологический университет им. Д.И. Менделеева (аспирант), Москва, Россия, Лебедев А.Е. (patlaten@yandex.ru) - Российский химико-технологический университет им. Д.И. Менделеева (аспирант), Москва, Россия, Малинина В.В. (patlaten@yandex.ru) - Российский химико-технологический университет им. Д.И. Менделеева (аспирант), Москва, Россия | |
| Ключевые слова: сверхкритический реактор., гидродинамика, математическое моделирование, аэрогель, сверхкритическая сушка, оптимизация, cfd fluent |
|
| Keywords: supercritical reactor, hydrodynamics, mathematical and computer modeling, aerogels, supercritical drying, optimisation, cfd fluent |
|
| Количество просмотров: 11962 |
Версия для печати Выпуск в формате PDF (9.63Мб) Скачать обложку в формате PDF (1.26Мб) |
Программный пакет Fluent 6.3.26 включает в себя набор базовых моделей для описания течения жидкостей, процессов тепло- и массопереноса и других процессов, некоторый набор численных методов решения обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, их систем, систем алгебраических уравнений, а также комплект инструментов для численного и графического анализа полученных результатов моделирования. Для решения дифференциальных уравнений в этом программном пакете используется метод конечных элементов. Суть его в преобразовании дифференциальных уравнений в частных производных в алгебраические уравнения. Вся исследуемая область пространства разбивается на ячейки (или клетки). Далее осуществляется интегрирование по объему каждой ячейки. Интегралы по объему, содержащие дивергенцию, преобразуются к интегралам по поверхности по теореме Остроградского–Гаусса. При этом все неизвестные заменяются соответствующими значениями в центре ячейки, которые найдены в результате решения полученных алгебраических уравнений. В данной работе описываются моделирование гидродинамики сверхкритического реактора с целью выбора его оптимальной геометрии и процесс сверхкритической сушки (или диффузионного замещения растворителя изопропилового спирта на сверхкритический диоксид углерода (СКДУ)) [1]. Сверхкритический реактор имеет следующие характеристики: длина L=0,105 м, диаметр D=0,055 м, диаметр входного и выходного штуцеров d=0,002 м. Внутри аппарата расположен пористый образец, имеющий форму цилиндра, диаметр которого равен 0,050 м, длина – 0,010 м. Для моделирования гидродинамики в сверхкритическом реакторе были сделаны следующие допущения: – весь аппарат заполнен СКДУ, пористый образец установлен на подложке; – аппарат работает в периодическом режиме, однако в модели рассматривается только стационарный период, соответствующий длительному процессу диффузионного замещения растворителя на СКДУ; – СКДУ является несжимаемой средой; – пористый слой учитывается в уравнении Дарси коэффициентом проницаемости; – распределительная решетка учитывается в уравнении Дарси соответствующим коэффициентом; – теплоперенос не учитывается, температура считается постоянной. Уравнения, описывающие гидродинамику внутри сверхкритического реактора [2, 3]:
дополнительные соотношения:
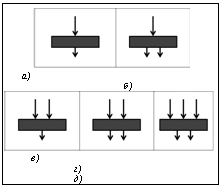
со следующими граничными условиями: Члены в правой части уравнения (2) (уравнения сохранения импульса) отвечают за изменение импульса при наличии градиента давления, сил трения, силы тяжести и других внешних сил соответственно. В данной модели дополнительная внешняя сила отражает вклад пористого тела в движение сплошной среды. Поток через пористый образец описывается уравнением Дарси. Для определения режима течения потока использован критерий Рейнольдса, который характеризует отношение инерционных сил, возникающих при движении среды, к силам вязкости. Впрыск СКДУ в объем аппарата производится со скоростью 0,018 м/с через входные патрубки. Линейная скорость в объеме аппарата значительно меньше, чем на входе. Значение критерия Рейнольдса для данной скорости равно: Re=ωdρ/µ= =397, где ω – линейная скорость потока, м/с; d – характерный размер потока (для потоков, протекающих во внутренней области цилиндрических объектов, равен внутреннему диаметру объекта), м; ρ – плотность сушильного агента, кг/м3; µ – динамическая вязкость сушильного агента, Па·с. Полученное значение критерия Рейнольдса говорит о том, что поток является ламинарным. Алгоритм решения уравнений модели Прежде всего необходимо определить алгоритм решения уравнений сохранения массы и импульса и вид, в котором эти уравнения будут представляться. Fluent предлагает два алгоритма решения – раздельный и совместный. Раздельный алгоритм подразумевает раздельное решение уравнений. Это приводит к тому, что приходится корректировать некоторые параметры, такие как давление, в результате число итераций увеличивается. При использовании совместного алгоритма решение сходится за меньшее число итераций, однако время, затрачиваемое на одну итерацию, возрастает ввиду усложнения процедуры решения. Модель гидродинамики является стационарной задачей, для нее выбран раздельный алгоритм расчета в неявном виде [2]. На рисунке 1 представлена блок-схема алгоритма. Цель моделирования – выбор оптимального расположения входных и выходных патрубков, а также их количества. Подача СКДУ осуществляется через входные патрубки, количество которых варьируется. Поток направлен вдоль оси симметрии аппарата и через него в выходные патрубки. Входная линейная скорость потока – 0,018 м/с, что соответствует расходу СКДУ 100 н.л/ч. Проведены расчеты для пяти вариантов геометрии (рис. 2) и расчет с распределительной решеткой внутри аппарата с геометрией «3–2» (расположение входов и выходов, как на рис. 2д). Она состоит из стальных колец Рашига 10×10×0,5 мм, имеет толщину 0,02 м. Для описания гидродинамики автоклав можно представить в виде цилиндра длиной 0,105 м и диаметром 0,055 м с различным количеством входов и выходов. Внутри основного цилиндра находится меньший цилиндр, описывающий пористый слой (аэрогель). Количество входов и выходов варьируется. Распределительная решетка в одном из вариантов геометрии установлена между входными отверстиями и пористым образцом. Это должно способствовать выравниванию скоростей СКДУ над пористым телом. Исходные данные Физико-химические свойства СКДУ при постоянных температуре 45 ºС и давлении 150 атм.: плотность – 818 кг/м3, вязкость – 0,000074 кг/м∙с. Построение расчетной сетки
Основным параметром расчетной сетки является ее плотность, потому что от нее зависит точность решения. Плотность расчетной сетки влияет и на время сходимости решения. При большом количестве ячеек для сходимости могут потребоваться значительные временные ресурсы. Поэтому приходится прибегать к различным способам уменьшения числа ячеек, основным из которых является снижение плотности сетки в областях, где поведение потоков в достаточной мере прогнозируемо или где можно пренебречь отклонениями. Была построена расчетная сетка, состоящая из тетраэдрических элементов с повышенной плотностью в области входных и выходных патрубков в объеме пористого тела. На начальном этапе расчетов максимальный шаг разбиения составлял 5 мм, минимальный – 1 мм. Время сходимости в данном случае составляет не более 20 минут, что является более чем приемлемой величиной. Для достижения заданной точности расчет проводился несколько раз для каждого варианта геометрии с изменением расчетной сетки – ее адаптацией. Эти решения последовательно сравнивались по значению средней скорости в образце геля. Повторные расчеты прекращались, когда значения средней скорости последнего и предыдущего расчетов отличались Результаты моделирования В результате расчета уравнений модели (уравнения (1), (2)), описывающих гидродинамику сплошной фазы, были получены распределение векторов скоростей по величине и направлению, а также гистограммы распределения значений скорости в объеме пористого образца. В процессе сушки в образце геля не должны образовываться зоны с существенно отличающимися концентрациями растворителя [4]. Для достижения такого результата распределение скоростей внутри образца должно быть как можно более равномерным. В качестве меры разброса скорости было выбрано среднеквадратичное отклонение (СКО). Наименьшее СКО достигается при использовании геометрии с тремя входами и двумя выходами, средняя скорость при использовании такой геометрии также наименьшая. Таким образом, оптимальным вариантом для геометрии реактора является вариант «3–2». Распределение скоростей неравномерное, наибольшие значения достигаются под центральным входом, тогда как боковые работают в некотором смысле вхолостую. Вместе с тем весь объем автоклава хорошо перемешан, застойные зоны отсутствуют.
Главная цель моделирования гидродинамики в данной работе – определить оптимальные параметры для реализации эффективного процесса сушки, при котором в монолите геля не образуются зоны с различной концентрацией растворителя. Предполагается, что мерой равномерности в расчетах может быть распределение скоростей внутри монолита [5]. Именно поэтому узость этого распределения была использована в качестве критерия пригодности той или иной геометрии. Количественной характеристикой разброса скоростей в настоящей работе выбрано СКО. В результате анализа результатов расчетов определено, что из вариантов с различным количеством входов и выходов вариант «3–2» является наилучшим в указанном выше смысле (СКО=9,6×10-7 м/с). Однако самое узкое распределение дает вариант с распределительной решеткой (СКО=2×10-8 м/с). То есть улучшение конструкции сверхкритического реактора может дать распределительная решетка, изготовление и использование которой не требуют серьезных конструктивных изменений. Литература 1. Smirnova I. Synthesis of silica aerogels and their application as a drug delivery system. PhD Thesis, Technical Univ. of Berlin. 2002. 2. Armfield S.W., Street R. Fractional step methods for the Navier-Stokes equations on non-staggered grids. J. of Comp. Phys. 1999. Vol. 153, pp. 660–665. 3. Jackson G.W., James D.F. The permeability of fibrous porous media. The Canadian J. of Chemical Engineering. 1986. Vol. 64, pp. 364–374. 4. Handbook of Sol-Gel Science and Technology: Processing, Characterization and Applications. Vol. I. Sol-Gel Processing. NY, Kluwert Acad. Publ. 2005. 1980 p. 5. Van der Spoel D., Lindahl E., Hess B. [at al.]. GROMACS: Fast, flexible and free. J. Comp. Chem. 2005, Vol. 26, pp. 1701–1718. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=3356 |
Версия для печати Выпуск в формате PDF (9.63Мб) Скачать обложку в формате PDF (1.26Мб) |
| Статья опубликована в выпуске журнала № 4 за 2012 год. [ на стр. 269-272 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Программный комплекс для расчета процесса нанесения покрытия в псевдоожиженном слое
- Типовые функции программного обеспечения рабочего места инструктора авиационного тренажера
- Система поддержки принятия решений по управлению информационными ресурсами
- Теоретический подход к управлению социально-техническими системами
- Репрезентативность метрик на основе событий процессора Intel Sandy Bridge при анализе времени обработки данных в памяти
Назад, к списку статей



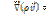 (1)
(1) (2)
(2) (3)
(3)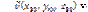
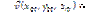 где ρ – плотность, кг/м3;
где ρ – плотность, кг/м3;  – вектор скорости, м/с; p – давление, Па;
– вектор скорости, м/с; p – давление, Па;  – дополнительный источник импульса, кг/м2∙с2;
– дополнительный источник импульса, кг/м2∙с2;  – коэффициент проницаемости, 1/м2;
– коэффициент проницаемости, 1/м2;  – значение вектора скорости на входе, м/с; r – радиус объекта сушки, м; (zпор2–zпор1) – длина объекта сушки, м; T – температура внутри аппарата, К; R – универсальная газовая постоянная, Дж/моль∙К; m – динамическая вязкость, кг/м∙с; переменные и величины с индексом «вх» относятся к входу непрерывной фазы в аппарат, а с индексом «ст» – к стенкам аппарата.
– значение вектора скорости на входе, м/с; r – радиус объекта сушки, м; (zпор2–zпор1) – длина объекта сушки, м; T – температура внутри аппарата, К; R – универсальная газовая постоянная, Дж/моль∙К; m – динамическая вязкость, кг/м∙с; переменные и величины с индексом «вх» относятся к входу непрерывной фазы в аппарат, а с индексом «ст» – к стенкам аппарата.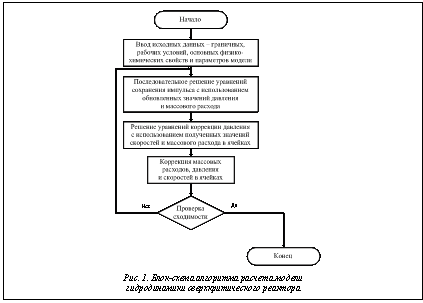
 друг от друга не более чем на 5 %. При проведении адаптации сетки программа разбивает помеченные ячейки на некоторое количество новых ячеек. Помечаются те ячейки, градиент определенного параметра (скорости, давления и т.п.) в которых больше заданного значения. Параметр и заданное значение определяются пользователем. В данной работе среднее значение скорости движения СКДУ по ячейкам пористого образца (аэрогеля) было принято за контрольный параметр.
друг от друга не более чем на 5 %. При проведении адаптации сетки программа разбивает помеченные ячейки на некоторое количество новых ячеек. Помечаются те ячейки, градиент определенного параметра (скорости, давления и т.п.) в которых больше заданного значения. Параметр и заданное значение определяются пользователем. В данной работе среднее значение скорости движения СКДУ по ячейкам пористого образца (аэрогеля) было принято за контрольный параметр. Моделирование гидродинамики потоков в сверхкритическом реакторе при наличии распределительной решетки проведено для оптимальной геометрии реактора «3–2» (рис. 3). Наличие распределительной решетки дает более близкий к идеальному вытеснению, то есть более равномерный, поток. Средняя скорость внутри монолита становится меньше, но распределение скорости более узкое. Средняя скорость в объеме аэрогеля составляет 1,4·10-8 м/с, а СКО – 2·10-8 м/с.
Моделирование гидродинамики потоков в сверхкритическом реакторе при наличии распределительной решетки проведено для оптимальной геометрии реактора «3–2» (рис. 3). Наличие распределительной решетки дает более близкий к идеальному вытеснению, то есть более равномерный, поток. Средняя скорость внутри монолита становится меньше, но распределение скорости более узкое. Средняя скорость в объеме аэрогеля составляет 1,4·10-8 м/с, а СКО – 2·10-8 м/с.