Путь к любому обоснованному заключению о стоимости лежит через решение ряда задач выбора, начиная от выбора базы оценки и заканчивая выбором согласованного результата. Для оценочной практики в целом характерна следующая ситуация. Имеется конечное множество альтернатив (вариантов), из которого нужно выбрать некоторое подмножество, в частном случае – одну альтернативу. Выбор производится на основе представлений о качестве и адекватности альтернатив (принципа оптимальности). Вот несколько типичных примеров:
– выбор лучшего наиболее эффективного использования недвижимости (ЛНЭИ);
– выбор объектов-аналогов на рынке недвижимости, компаний-аналогов на фондовом рынке;
– выбор подходящих ставок капитализации, ставок дисконта, мультипликаторов;
– выбор сценариев денежных потоков, схем инвестирования, финансирования;
– выбор адекватных методов расчета стоимости, рыночных формул;
– выбор информационной базы.
Альтернативы в оценочной практике – это экономические объекты, рыночные и финансовые показатели, информационные ресурсы, формулы и методы расчета стоимости. Они могут быть наделены внутренней структурой, нередко иерархической.
Альтернативы обладают многими свойствами, которые в ходе выбора должны учитываться совместно. Простые свойства однозначно представляются числами. Такие свойства называются критериями. Сложные свойства могут не допускать числового представления. Их называют аспектами. Качественные свойства и группы критериев являются аспектами. Критерий – это частный случай аспекта.
Задача выбора считается простой, если имеется только один аспект, позволяющий сравнить любые две альтернативы и непосредственно указать, какая из них лучше. Решение простых задач очевидно. Простые задачи сами по себе интереса не представляют. Они рассматриваются как предельный случай реальных задач выбора.
В реальных задачах выделить какой-либо один аспект не удается. Более того, часто вообще трудно выделить аспекты. Выделение и ранжирование аспектов, существенных для последующего выбора, в свою очередь, есть задача выбора. Если некоторые из аспектов важнее (приоритетнее) других аспектов, это обстоятельство должно учитываться в математической модели выбора.
Задачей выбора называется алгебра , где W – множество альтернатив, ОП – принцип оптимальности. Задача имеет смысл, если множество альтернатив известно. Принцип оптимальности, как правило, неизвестен. Поэтому на практике выбор производит ЛПР лично или с привлечением экспертов. В оценочной практике ЛПР – это оценщик. Именно здесь кроется один из источников субъективизма, который делает оценки невоспроизводимыми.
Кроме того, субъективная природа выбора не всегда позволяет наилучшим образом использовать исходный информационный ресурс – множество W, что, в свою очередь, приводит к уменьшению достоверности получаемых оценок.
Предлагаемый в настоящей работе подход к решению задач выбора не подразумевает знания ОП. Покажем, что при естественных предположениях относительно W и ОП решение существует и достигается без участия ЛПР и экспертов.
Постановка задачи
Математическим выражением принципа оптимальности служит функция выбора. Функция выбора C(X) сопоставляет любому множеству ХÍW его часть. C(X) интерпретируется как множество наиболее предпочтительных элементов X. Решение исходной задачи выбора есть множество C(W). Сравнение альтернатив между собой осуществляется при помощи бинарных отношений. Всякое бинарное отношение R на множестве X порождает функцию выбора CR(X) по правилу
 , (1)
, (1)
где 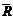 – дополнение к R.
– дополнение к R.
Функции выбора, порожденные бинарным отношением, называются нормальными. Не всякая функция выбора является нормальной, но всякая может быть представлена в виде логической композиции нормальных [1].
С вычислительной точки зрения бинарные отношения и функции выбора реализуются семействами логических функций и называются логической формой отношения (ЛФО) и логической формой выбора (ЛФВ) соответственно. Бинарные отношения и функции выбора обеспечивают математический аппарат, формализующий процесс сравнения и выбора альтернатив.
В настоящей работе изучаются следующие два вопроса.
1. Свойства, которыми должны обладать W, ОП, функции выбора и бинарные отношения для того, чтобы решение задачи выбора существовало при любых W¹Æ, соответствовало целям и задачам оценочной деятельности, было логически обосновано (непротиворечиво).
2. Алгоритмические подходы к решению задач выбора, возникающих в оценочной деятельности.
Существование выбора
Не всякая интуитивно ясная функция выбора обеспечивает реальный выбор. Яркий пример тому – функция выбора, порожденная мажоритарным бинарным отношением. При сравнении по мажоритарному отношению предпочтение отдается той из альтернатив, которая лучше по большинству аспектов (модель голосования). Несмотря на свою популярность, данный принцип может приводить к пустому выбору уже для множества из трех элементов, если их отношения образуют цикл.
Будем считать, что решение задачи выбора существует, если выбор из W отличен от пустого множества при любых W¹Æ. То есть выбор возможен всегда, когда есть хотя бы одна альтернатива.
Для нормальных функций выбора необходимые и достаточные условия существования решения дает утверждение 1: функция выбора CR(X)¹Æ для любого множества X¹Æ тогда и только тогда, когда порождающее ее отношение R ациклично [1].
Ацикличность отношения – это свойство фундаментальное и к другим свойствам не сводится. Когда отношение задано графом, тестирование графа на цикличность выполняется на компьютере при помощи стандартных рекурсивных алгоритмов. Достаточными условиями ацикличности отношения являются его транзитивность и антирефлексивность. Эти два свойства легко проверяются по матрице отношения R={rij}. На главной диагонали матрицы антирефлексивного отношения должны стоять нули. Транзитивность имеет место, если для любых i, k выполнено 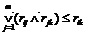 .
.
Транзитивность и ацикличность отражают естественные логические взаимосвязи между альтернативами. Действительно, если альтернатива x в каком-то смысле лучше альтернативы y, а y в том же смысле лучше z, то естественно считать, что x в этом же смысле лучше z (транзитивность). И во всяком случае z не лучше x (ацикличность). Ясно, что наличие у отношения свойств транзитивности и ацикличности связано не только с вопросом существования решения, но и с логической непротиворечивостью функций выбора, которые порождены этим отношением.
Мажоритарное отношение свойствами транзитивности и ацикличности не обладает.
Логическая обоснованность выбора
Если в процессе выбора альтернатив учитывать m аспектов, то имеется  различных функций выбора [1]. Не все из них одинаково полезны. Выбор может быть признан логически обоснованным, только если при изменении X значения функции выбора C(X) меняются непротиворечивым образом. Рассмотрим пример.
различных функций выбора [1]. Не все из них одинаково полезны. Выбор может быть признан логически обоснованным, только если при изменении X значения функции выбора C(X) меняются непротиворечивым образом. Рассмотрим пример.
Допустим, что X¢ – множество информационных ресурсов, которые до некоторого момента использовались при оценке собственности. Затем это множество расширилось за счет добавления новых ресурсов. Обозначим новое множество X, X¢ÍX. Обязан ли выбор из нового множества X включать те элементы, которые выбирались из старого множества X¢ до его расширения? Ясно, что нет. Новый выбор не зависит от старого. Монотонность функции C(X) здесь не требуется.
Теперь предположим, что в новый выбор C(X) попали некоторые элементы X¢, то есть C(X)ÇX¢¹Æ. Логично предположить, что эти элементы выбирались и ранее, до расширения X¢. Тогда выполняется условие наследования
X¢ÍXÞC(X)ÇX¢ÍC(X¢). (2)
Пусть выбор из нового множества C(X) оказался таким, что все выбранные элементы ранее уже присутствовали в X¢, то есть C(X)ÍX¢ÍX. В данной ситуации естественно допустить, что результаты выбора до и после расширения множества X¢ должны совпадать. Тогда выполняется условие независимости от отвергнутых альтернатив:
C(X)ÍX¢ÍXÞC(X¢)=С(X). (3)
Условие согласия означает, что альтернативы, которые были выбраны из каждого множества Xi, будут выбраны из их объединения:
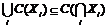 . (4)
. (4)
Отказ от выполнения условий (2)–(4) приводит к тому, что функция выбора C(X) становится контекстно-зависимой. Пример контекстно-зависимых функций выбора дают спортивные турниры, когда положение каждой команды в турнирной таблице зависит не только от ее собственной игры, но и от результатов встреч других команд между собой.
Контекстно-зависимые функции выбора применяются в социологии, филологии, психологии, политологии и других областях, где выбор и интерпретация объекта обусловлены свойствами не только самого объекта, но и его окружения.
Оценочная деятельность подразумевает независимость и объективность при анализе рыночной среды, выборе методов расчета стоимости, использовании информационных ресурсов. Также весьма желательна воспроизводимость оценок.
Эти соображения приводят к выводу, что целям и задачам оценочной деятельности соответствуют контекстно-независимые функции выбора, удовлетворяющие условиям (2)–(4). В пользу контекстно-независимых функций выбора также говорит их полная логическая прозрачность. Последнее обстоятельство становится решающим, когда возникает необходимость доказательства заказчикам и третьим лицам обоснованности и непротиворечивости сделанных выборов.
Структуру класса контекстно-назависимых функций выбора устанавливает утверждение 2: класс функций выбора, обладающих свойствами (2)–(4), совпадает с классом нормальных функций выбора, порожденных транзитивными антирефлексивными бинарными отношениями.
Из класса транзитивных антирефлексивных бинарных отношений выделим отношение Парето (Р) и отношение лексикографии (L) в евклидовом пространстве Em, которые затем используем для конструирования иерархических отношений специального вида.
Отношение Парето (Р) определяется следующим образом:

Множеством Р-оптимальных элементов на W является множество Парето WP:
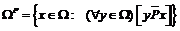 .
.
Отношение лексикографии (L) определяется следующим образом. Пусть на осях координат задан такой линейный порядок, что k1>k2>…>km, где ki – номер координаты на i-м месте порядка. Тогда
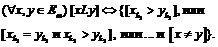
Множество L-оптимальных элементов всегда состоит из единственного элемента.
Отношение Парето обеспечивает универсальную математическую модель контекстно-независимого выбора, а отношение лексикографии – математическую модель упорядочения аспектов по важности при контекстно-независимом выборе.
Различные логические композиции бинарных отношений P и L моделируют широкий класс ситуаций выбора, которые возникают в оценочной практике.
Решение задач выбора
Процесс решения задачи традиционно организуют в два этапа: сначала формируют множество альтернатив W, а затем решают задачу выбора.
В процессе формирования множества W используют условия допустимости альтернатив, которые определяются исходя из конкретных условий задачи или общих соображений. При этом считается всегда известным универсальное множество WУ всех мыслимых альтернатив. Задача формирования W является задачей выбора , где ОП1 – принцип оптимальности, выражающий условия допустимости альтернатив. Множество  , полученное в результате решения указанной задачи выбора, называют исходным множеством альтернатив (ИМА).
, полученное в результате решения указанной задачи выбора, называют исходным множеством альтернатив (ИМА).
Часто условия допустимости альтернатив не удается сформулировать явно. Тогда отношение Парето дает естественный принцип оптимальности ОП1 для нахождения ИМА. Действительно, если цель состоит в выборе лучших альтернатив по всей совокупности аспектов (принцип ЛНЭИ), то заведомо нет необходимости включать в ИМА доминируемые альтернативы, которые не входят в множество Парето. Они по определению никог- да не попадут в число лучших, однако способны увеличить дисперсию при статистической обработке W. Применительно к оценочной практике доминируемые альтернативы играют роль информационного мусора. Здесь может быть уместна аналогия с теорией игр, где доминируемые стратегии исключаются из рассмотрения по мере их выявления [2].
Для дальнейшего изложения будем считать, что каждая альтернатива xÎW характеризуется конечным набором значений аспектов x=(x1, x2, …, xm).
Обозначим А={1, ..., m} множество номеров аспектов, учитываемых при выборе, {A} – множество всех подмножеств A.
Можно считать, что выбор между любыми двумя альтернативами x и y при учете только одного любого аспекта является простой задачей. Если это не так, соответствующий аспект всегда может быть подвергнут декомпозиции и представлен в виде группы более простых аспектов [1].
Для каждой пары альтернатив (x, y) определим семейство функций aj(x, y):
 ; jÎA. (5)
; jÎA. (5)
Если x и y равноценны по некоторому аспекту с номером j, то для такого номера j функция aj(x, y) не определена.
Сформируем множество J номеров тех аспектов, по которым x и y отличаются:
 ; jÎ{A}. (6)
; jÎ{A}. (6)
Далее рассматриваются типичные задачи выбора, строятся адекватные иерархические бинарные отношения R, приводятся соответствующие ЛФО и алгоритмы проверки соотношения xRy. Решение собственно задач выбора находят как множество значений соответствующей функции выбора.
Аспекты упорядочены по важности
Допустим, имеется априорная информация о важности аспектов и она такова, что аспекты можно разбить на n непересекающихся множеств (групп). Внутри одной и той же группы любые два аспекта равноценны. Сказанное означает, что
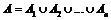 ; n£m; AiÇAk=Æ;
; n£m; AiÇAk=Æ; 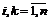 .
.
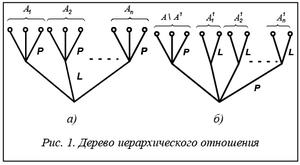
 Здесь Ai – непересекающиеся множества (группы) номеров аспектов одинаковой важности. Без ограничения общности можно считать, что группы Ai отсортированы в порядке убывания важности аспектов. На основании информации о важности аспектов строится дерево иерархического отношения R (см. рис. 1а).
Здесь Ai – непересекающиеся множества (группы) номеров аспектов одинаковой важности. Без ограничения общности можно считать, что группы Ai отсортированы в порядке убывания важности аспектов. На основании информации о важности аспектов строится дерево иерархического отношения R (см. рис. 1а).
Если x, y – две альтернативы, то для проверки соотношения xRy применяется алгоритм 1.
Шаг 1. По формулам (5) и (6) вычислить значения aj(x, y) и множество J.
Шаг 2. Образовать множества Bi=AiÇJ, 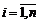 , I={i: Bi¹Æ}. По построению I – это упорядоченное множество номеров групп, таких, что x отличается от y хотя бы по одному аспекту внутри каждой из групп, причем группы более важных аспектов имеют меньший номер.
, I={i: Bi¹Æ}. По построению I – это упорядоченное множество номеров групп, таких, что x отличается от y хотя бы по одному аспекту внутри каждой из групп, причем группы более важных аспектов имеют меньший номер.
Шаг 3. Для каждого непустого Bi вычислить значения ЛФО Парето:  .
.
Шаг 4. Итоговый результат есть значение ЛФО лексикографии на I: xRy .
.
Проверив выполнение отношения xRy для каждой пары (x, y), строят матрицы отношений R и 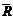 . Затем по формуле (1) находят решение задачи выбора.
. Затем по формуле (1) находят решение задачи выбора.
Сравнительная важность для некоторых пар аспектов
Предположим, что для n пар аспектов известна их сравнительная важность. Для другой части аспектов подобная информация отсутствует. Введем обозначения:
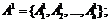
 pi, qiÎA;
pi, qiÎA;  .
.
Здесь 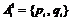 – пары номеров аспектов, таких, что аспект с номером pi важнее аспекта с номером qi. На основании информации о важности аспектов строится дерево иерархического отношения R (см. рис. 1б)
– пары номеров аспектов, таких, что аспект с номером pi важнее аспекта с номером qi. На основании информации о важности аспектов строится дерево иерархического отношения R (см. рис. 1б)
 В качестве примера приведем результаты выбора аналогов для гипотетической оцениваемой компании по производству строительных материалов. Для наглядного представления данных число учитываемых аспектов искусственно ограничено десятью.
В качестве примера приведем результаты выбора аналогов для гипотетической оцениваемой компании по производству строительных материалов. Для наглядного представления данных число учитываемых аспектов искусственно ограничено десятью.
Учитываются пять показателей из балансового отчета и пять показателей из отчета о прибылях и убытках. Таким образом, десять показателей определяют профиль каждой компании. На рисунке 2 профили компаний представлены в виде объемных графиков. Первым слева показан профиль объекта оценки, затем десять профилей компаний-аналогов, вошедших в исходное множество альтернатив (ИМА).
В качестве ИМА здесь принято множество Парето всех компаний отрасли, акции которых котируются на NYSE (Нью-Йоркская фондовая биржа).
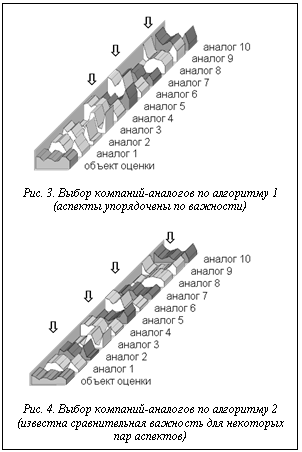
На первом этапе все десять учитываемых аспектов были разбиты по важности на три непересекающиеся группы. Наибольший приоритет был придан показателям доходности и объемам продаж. Затем по алгоритму 1 был произведен выбор (рис. 3).
Отобранные компании-аналоги на рисунке 4 выделены стрелками и более темным цветом. В адекватности произведенного выбора можно убедиться визуально. Профили выбранных компаний-аналогов в наибольшей мере сходны с профилем объекта оценки. Количество отобранных аналогов существенно зависит от структуры разбиения аспектов на группы.
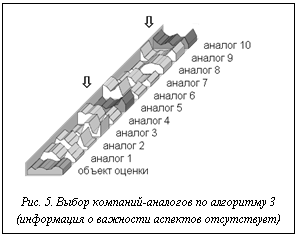
На втором этапе для некоторых из аспектов была указана их сравнительная важность посредством задания пар номеров аспектов так, что в каждой паре первый аспект важнее второго. Таким образом, задано частичное бинарное отношение на множестве номеров аспектов. Если отношение не является цикличным (непротиворечиво), выбор может быть осуществлен по алгоритму 2. Выбранные аналоги представлены на рисунке 4, они выделены стрелками и более темным цветом.
 Для преодоления этой дилеммы предложен подход, основанный на применении контекстно-независимых функций выбора и бинарных отношений специального вида. Его использование позволяет уменьшить субъективизм оценок и одновременно исключить или свести к минимуму роль экспертных процедур.
Для преодоления этой дилеммы предложен подход, основанный на применении контекстно-независимых функций выбора и бинарных отношений специального вида. Его использование позволяет уменьшить субъективизм оценок и одновременно исключить или свести к минимуму роль экспертных процедур.
Литература
1. Макаров И.М., Виноградская Т.М., Рубчинский А.А., Соколов В.Б. Теория выбора и принятия решений: Учеб. пособие для вузов. М.: Наука, 1982. 327 с.
2. Исследование операций; [под ред. Дж. Моудера, С. Элмаграби]. В 2-х т. Т. 1: Методологические основы и математические методы. М.: Мир, 1981. 712 с.
3. Тельнов В.П., Тришин В.Н. Задачи выбора в оценочной деятельности: тез. докл. II Междунар. конф. по проблемам управления. М.: Изд-во ИПУ РАН, 2003. С. 187.
References
1. Makarov I.M., Vinogradskaya T.M., Rubchinsky A.A., Sokolov V.B., Teoriya vybora i prinyatiya resheniy: ucheb. posobie dlya vuzov [The theory of decision making], Moscow, Nauka, 1982, 327 p.
2. Moder J., Elmaghraby S., Handbook of Operations Re-search, Vol. 1, Business & Economics, 1978, 659 p.
3. Telnov V.P., Trishin V.N., Tez. dokl. II mezhdunar. konf. po problemam upravleniya [Proc. 2 Int. Conf. on management prob-lems], Vol. 3, Moscow, ICS RAS Publ., 2003, 187 p.



 , (1)
, (1)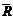 – дополнение к R.
– дополнение к R.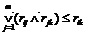 .
. различных функций выбора [1]. Не все из них одинаково полезны. Выбор может быть признан логически обоснованным, только если при изменении X значения функции выбора C(X) меняются непротиворечивым образом. Рассмотрим пример.
различных функций выбора [1]. Не все из них одинаково полезны. Выбор может быть признан логически обоснованным, только если при изменении X значения функции выбора C(X) меняются непротиворечивым образом. Рассмотрим пример.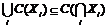 . (4)
. (4)
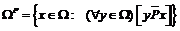 .
.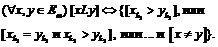
 , полученное в результате решения указанной задачи выбора, называют исходным множеством альтернатив (ИМА).
, полученное в результате решения указанной задачи выбора, называют исходным множеством альтернатив (ИМА). ; jÎA. (5)
; jÎA. (5) ; jÎ{A}. (6)
; jÎ{A}. (6)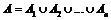 ; n£m; AiÇAk=Æ;
; n£m; AiÇAk=Æ; 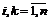 .
.

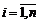 , I={i: Bi¹Æ}. По построению I – это упорядоченное множество номеров групп, таких, что x отличается от y хотя бы по одному аспекту внутри каждой из групп, причем группы более важных аспектов имеют меньший номер.
, I={i: Bi¹Æ}. По построению I – это упорядоченное множество номеров групп, таких, что x отличается от y хотя бы по одному аспекту внутри каждой из групп, причем группы более важных аспектов имеют меньший номер. .
. .
.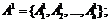
 pi, qiÎA;
pi, qiÎA;  .
.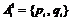 – пары номеров аспектов, таких, что аспект с номером pi важнее аспекта с номером qi. На основании информации о важности аспектов строится дерево иерархического отношения R (см. рис. 1б)
– пары номеров аспектов, таких, что аспект с номером pi важнее аспекта с номером qi. На основании информации о важности аспектов строится дерево иерархического отношения R (см. рис. 1б) В качестве примера приведем результаты выбора аналогов для гипотетической оцениваемой компании по производству строительных материалов. Для наглядного представления данных число учитываемых аспектов искусственно ограничено десятью.
В качестве примера приведем результаты выбора аналогов для гипотетической оцениваемой компании по производству строительных материалов. Для наглядного представления данных число учитываемых аспектов искусственно ограничено десятью. Для преодоления этой дилеммы предложен подход, основанный на применении контекстно-независимых функций выбора и бинарных отношений специального вида. Его использование позволяет уменьшить субъективизм оценок и одновременно исключить или свести к минимуму роль экспертных процедур.
Для преодоления этой дилеммы предложен подход, основанный на применении контекстно-независимых функций выбора и бинарных отношений специального вида. Его использование позволяет уменьшить субъективизм оценок и одновременно исключить или свести к минимуму роль экспертных процедур.