Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Комплексный метод выполнения арифметических операций над нечеткими числами и его применение при экономическом анализе в условиях неопределенности
Аннотация:Аппарат нечеткой логики широко используется при математическом описании сложных систем в условиях неопределенности, позволяя описывать знания, представленные в качественной форме, не требуя выполнения предпосылок применимости теории вероятностей. Нечеткие числа LR-типа – это разновидность нечетких чисел специального вида, задаваемых по определенным правилам с целью снижения объема вычислений при операциях над ними. В статье доказана теорема, позволяющая сводить арифметические операции над симметричными нечеткими числами LR-типа (сложение, умножение, нахождение противоположного и обратного элементов) к арифметическим операциям над комплексными числами. Приведена графическая иллюстрация выполнения арифметических операций сложения и вычитания над нечеткими числами на комплексной плоскости, что дает возможность производить эти операции графическим методом. Как известно, широко распространенные системы компьютерной математики (MATLAB, MathCAD, Maple и др.) содержат средства, позволяющие выполнять арифметические операции над комплексными числами, причем как в численном, так и в символьном виде. В то же время указанные системы компьютерной математики в своей стандартной комплектации не содержат средства выполнения арифметических операций над нечеткими числами. Приведенная в статье теорема позволяет достаточно просто использовать указанные системы в практике расчетов с нечеткими числами. В качестве примера вычислений рассматривается расчет чистого приведенного дохода в условиях неопределенности. В частности, предполагается, что поступления от инвестиционного проекта, отток денежных средств и индекс инфляции заданы симметричными нечеткими числами LR-типа.
Abstract:Fuzzy logic is widely used in the mathematical description of complex systems under uncertainty. It allows to describe the knowledge presented in a qualitative way without requiring the implementation of the applicability prerequisites of the theory of probability. LR-type fuzzy numbers are a type of fuzzy numbers defined according to certain rules in order to reduce the amount of computation in operations. The article describes and proves a theorem that allows to convert the arithmetic operations with LR-type symmetric fuzzy numbers (addition, multiplication, finding the opposite and inverse elements) to arithmetic operations with complex numbers. The article shows a graphic illustration of the arithmetic operations of fuzzy numbers adding and subtracting in the complex plane which makes it possible to make these arithmetic operations graphically. As it known, widely distributed computer math systems (MATLAB, MathCAD, Maple etc.) have the means to perform arithmetic operations with complex numbers, both in numbers and in symbolic form. At the same time, standard configuration of these systems does not contain tools to perform arithmetic operations with fuzzy numbers. The theorem proposed in the article can simply use these systems in practical calculations with fuzzy numbers. There is an example of net present value calculation under uncertainty. In particular, it is assumed that the investment project income, the money outflow and inflation rate are set by LR-type symmetrical fuzzy numbers.
| Авторы: Усков А.А. (prof.uskov@gmail.com) - Российский университет кооперации, г. Мытищи, Россия, доктор технических наук, Киселев И.А. () - Российский университет кооперации, г. Мытищи, Россия, Аспирант | |
| Ключевые слова: нечеткие, неопределенность, комплексные числа, нечеткая логика, экономический анализ |
|
| Keywords: fuzzy numbers, uncertainty, complex numbers, fuzzy logic, economic analysis |
|
| Количество просмотров: 11315 |
Версия для печати Выпуск в формате PDF (7.68Мб) Скачать обложку в формате PDF (1.35Мб) |
Аппарат нечеткой логики широко используется при математическом описании сложных систем в условиях неопределенности, позволяя формализовывать знания, представленные в качественной форме, и не требуя выполнения предпосылок применимости теории вероятностей [1–3]. Нечеткие числа – нечеткие переменные, определенные на числовой оси, то есть нечеткое число определяется как нечеткое множество А на множестве действительных чисел R с функцией принадлежности μA(x)Î[0, 1], где x – действительное число, то есть xÎR [2, 3]. Нечеткие числа LR-типа – это разновидность нечетких чисел специального вида, то есть задаваемых по определенным правилам с целью снижения объема вычислений при операциях над ними [2, 3]. Функции принадлежности нечетких чисел LR-типа задаются с помощью не возрастающих на множестве неотрицательных действительных чисел функций действительных переменных L(x) и R(x), удовлетворяющих свойствам: а) L(–x)=L(x), R(–x)=R(x); б) L(0)=R(0). Пусть L(x) и R(x) – функции LR-типа. Унимодальное нечеткое число А с модой а (то есть μA(a)=1) c помощью L(x) и R(x) задается следующим образом: μA(x)= где а – мода; a>0, b>0 – левый и правый коэффициенты нечеткости. Таким образом, при заданных L(x) и R(x) нечеткое число задается тройкой (а, a, b). Предположим, имеются нечеткие числа LR-типа Арифметические операции над нечеткими LR-числами определяются следующим образом: (m, a, b)LR+(n, g, d)LR=(m+n, a+g, b+d)LR, (m, a, b)LR×(n, g, d)LR=(mn, an+gm, bn+dm)LR,
–(m, a, b)LR= (–m, b, a)LR, (m, a, b)–1LR= Нечеткое число Теорема. Пусть имеются симметричные нечеткие числа LR-типа: Тогда арифметические операции над симметричными нечеткими числами LR-типа Доказательство. Сравним результаты арифметических операций над нечеткими числами
a+b=(m+n)+j(a+g). Таким образом, С учетом того, что для нечетких чисел m×n>>a×g, в практических расчетах можно считать a×b»m×n+j(m×g+n×a). Таким образом, Таким образом, – С учетом того, что для нечетких чисел
Теорема доказана. На рисунке показана графическая иллюстрация выполнения арифметических операций сложения и вычитания над нечеткими числами на комплексной плоскости. Как известно, широко распространенные системы компьютерной математики (MATLAB, MathCAD, Maple и др.) содержат средства, позволяющие выполнять арифметические операции над комплексными числами, причем как в численном, так и в символьном виде. В то же время указанные системы компьютерной математики в своей стандартной комплектации не содержат средства выполнения арифметических операций над нечеткими числами. Приведенная ранее теорема поз- воляет сводить арифметические операции над симметричными нечеткими числами LR-типа к арифметическим операциям над комплексными числами. В качестве примера рассмотрим расчет чистого приведенного дохода в условиях неопределенности [5]. Предположим, что поступления от инвестиционного проекта
Для расчета комплексным методом согласно доказанной теореме необходимо произвести следующие действия: – перейти от нечетких чисел к комплексным: – произвести вычисления по формуле
– осуществить обратный переход от комплексных чисел к нечетким:
Литература 1. Усков А.А., Кузьмин А.В. Интеллектуальные технологии управления. Искусственные нейронные сети и нечеткая логика. М.: Горячая Линия–Телеком, 2004. 2. Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях. Тюмень: Изд-во Тюменского гос. ун-та, 2000. 3. Круглов В.В., Усков А.А. Два подхода к самоорганизации базы правил системы нечеткого логического вывода // Информационные технологии. 2006. № 2. С. 14–18. 4. Берд Дж. Инженерная математика. М.: Додэка-XXI, 2008. (Сер. Карманный справочник). 5. Кучарина Е.А. Инвестиционный анализ. СПб: Пи- тер, 2006. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=3487 |
Версия для печати Выпуск в формате PDF (7.68Мб) Скачать обложку в формате PDF (1.35Мб) |
| Статья опубликована в выпуске журнала № 2 за 2013 год. [ на стр. 175-178 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Организация адаптивной маршрутизации данных в электроэнергетических комплексах с использованием онтологических нечетких классификаторов
- Модель выбора мероприятий по обеспечению информационной безопасности на основе нечетких автоматов
- Основы структурно-лингвистического подхода в анализе нечетких временных рядов
- Структурная схема нечеткого регулятора на основе лингвистических переменных с четкими термами
- Программный пакет анализа эффективности инвестиционных проектов на основе нечетких вычислений
Назад, к списку статей



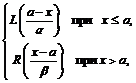
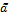 =(m, a, b)LR и
=(m, a, b)LR и  =(n, g, d)LR.
=(n, g, d)LR. >0,
>0, 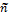 >0
>0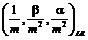 ,
,  =(m, a, b)LR – симметричное нечеткое число LR-типа, если a=b.
=(m, a, b)LR – симметричное нечеткое число LR-типа, если a=b.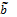 «b=n+jg, где j=
«b=n+jg, где j= .
.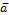 ,
,  ,
,  , где
, где 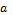 .
.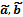 и их комплексными изображениями
и их комплексными изображениями 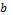 [2–4]:
[2–4]: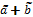 =(m+n, a+g, a+g)LR,
=(m+n, a+g, a+g)LR, =–m+j×a.
=–m+j×a.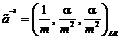 , m>0,
, m>0, 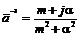 .
. , в практических расчетах можно считать
, в практических расчетах можно считать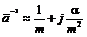 ,
, 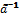 «
«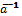 .
.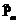 , отток денежных средств
, отток денежных средств 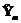 и индекс инфляции
и индекс инфляции 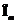 в m-м месяце заданы симметричными нечеткими числами LR-типа. Формула чистого приведенного дохода за N месяцев имеет вид [5]
в m-м месяце заданы симметричными нечеткими числами LR-типа. Формула чистого приведенного дохода за N месяцев имеет вид [5]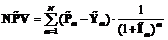 .
.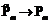 ,
, 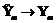 ,
,  ;
;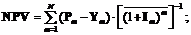
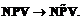
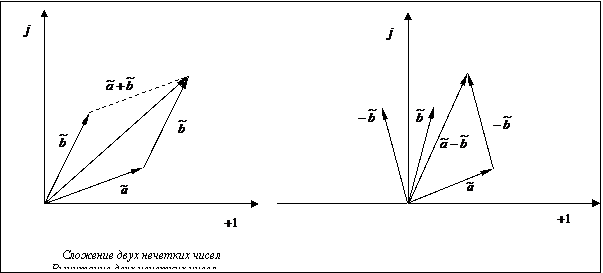 Приведенные в статье результаты позволяют упростить использование систем компьютерной математики (MATLAB, MathCAD, Maple и др.) в практике нечеткого моделирования и представлять результаты расчетов в наглядной форме в виде векторных диаграмм на комплексной плоскости.
Приведенные в статье результаты позволяют упростить использование систем компьютерной математики (MATLAB, MathCAD, Maple и др.) в практике нечеткого моделирования и представлять результаты расчетов в наглядной форме в виде векторных диаграмм на комплексной плоскости.