Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Программный пакет анализа эффективности инвестиционных проектов на основе нечетких вычислений
Аннотация:В статье рассмотрены программный пакет «Анализ эффективности инвестиционных проектов с привлечением заемных средств» и его математическое обеспечение. С помощью разработанного программного пакета можно в условиях неопределенности оценивать такие показатели эффективности инвестиционных проектов, как степень устойчивости инвестиционного проекта, наименьший срок погашения кредита, чистый приведенный доход, внутренняя норма доходности. Инвестиционная деятельность всегда ведется в условиях неопределенности: точно не известны будущие денежные поступления от реализации инвестиционного проекта, индекс инфляции и некоторые другие показатели. В рассматриваемом программном пакете неопределенность учитывается путем введения в расчетные формулы нечетких переменных в виде нечетких чисел LR-типа, параметры которых должны быть оценены предварительно, например экспертным методом. Предложена формула на основе арифметики нечетких чисел LR-типа для расчета чистого приведенного дохода от инвестиционного проекта при привлечении заемных средств. Данная формула отличается учетом параметров кредита, что позволяет совместно оценивать выбор инвестиционного проекта и условий получения кредита для его финансирования из множества доступных при неопределенности нечеткого характера.
Abstract:The article offers a formula for calculating net present value of the investment project using loan capital. This formula is different within the parameters of the loan, so you can conjointly evaluate the choice of the investment project and loan conditions to finance it under uncertainty. Investment activity is always conducted under uncertainty: future investment project cash flows, the inflation rate and other indicators are uncertain. In proposed software package the uncertainty is taken into account by putting fuzzy variables into the formulas in the form of LR-type fuzzy numbers. Their parameters have to be assessed in advance, for example, using expert method. Using LR-type fuzzy numbers allows simplifying formulas. As an intermediate result, a formula for the construction of LR-type fuzzy numbers is in the whole positive degree. The numerical example is made in the system of computer mathematics Mathcad to illustrate the practical implementa-tion of net present value calculation. Based on these results a software package «The investment projects analysis with bor-rowed funds» has been developed. The developed software package helps to estimate indexes of effectiveness under uncertainty: investment project stability margin, minimal loan maturity, net present value, internal rate of return. These results may be useful in the investment analysis practice.
| Авторы: Усков А.А. (prof.uskov@gmail.com) - Российский университет кооперации, г. Мытищи, Россия, доктор технических наук, Киселев И.А. () - Российский университет кооперации, г. Мытищи, Россия, Аспирант , Кондратова Н.В. () - Российский университет кооперации (аспирант ), г. Мытищи, Россия | |
| Ключевые слова: чистый приведенный доход., нечеткое число, неопределенность, инвестиционный проект |
|
| Keywords: net present value, fuzzy number, uncertainty, investment project |
|
| Количество просмотров: 11155 |
Версия для печати Выпуск в формате PDF (7.68Мб) Скачать обложку в формате PDF (1.35Мб) |
Одной из основных целей инвестиционной деятельности является достижение наилучших результатов капиталовложений, поэтому особое место отводится правильной оценке эффективности инвестиционного проекта (ИП). Реализация большинства ИП требует привлечения заемного капитала. В связи с этим весьма актуальной представляется задача принятия решений по наиболее эффективному использованию заемных средств. Для ее решения был разработан специализированный программный пакет «Анализ эффективности инвестиционных проектов с привлечением заемных средств» (Свид. о гос. регистр. прогр. для ЭВМ № 20126144635 от 24.05.2012, авторы: А.А. Усков, О.В. Балашов, И.А. Киселев). Под задачей управления заемными средствами в настоящей статье понимается совокупность взаимосвязанных задач: оптимальный выбор ИП, его параметров и условий кредита для его финансирования из множества допустимых. Отметим, что оптимальное решение указанных задач может быть найдено для них только совместно, так как важны не только показатели эффективности ИП, но и стоимость кредита для его реализации, например, высокоэффективный ИП совместно с дорогим кредитом может оказаться менее эффективным по сравнению с низкоэффективным ИП, под который имеется дешевый кредит. Инвестиционная деятельность всегда ведется в условиях неопределенности: точно не известны будущие денежные поступления от реализации ИП, индекс инфляции и некоторые другие показатели. В рассматриваемом программном продукте неопределенность учитывается путем введения в расчетные формулы нечетких переменных в виде нечетких чисел LR-типа, параметры которых должны быть оценены предварительно, например экспертным методом. Использование нечетких чисел LR-типа позволяет существенно упростить расчетные формулы. С помощью разработанного программного пакета можно в условиях неопределенности нечеткого характера оценивать следующие показатели эффективности ИП: – степень устойчивости ИП – показывает его финансовую реализуемость, а именно, на сколько процентов поступления от ИП будут больше, чем требуемые платежи по кредиту, полученному под реализацию данного ИП; – наименьший срок погашения кредита – время погашения кредита для случая, когда все поступления от ИП идут на погашение кредита; – чистый приведенный доход – доход с учетом оттока денежных средств и инфляции; – внутренняя норма доходности – параметр, показывающий, при какой процентной ставке по кредиту чистый приведенный доход от ИП будет равен 0. Рассмотрим математическое обеспечение расчета чистого приведенного дохода. Постановка задачи Предположим, что ИП требует однократного первоначального вложения капитала в сумме K. Данная сумма получена в кредит под R процентов годовых на MКР месяцев. Все платежи равные (аннуитетные), и разрешено досрочное погашение кредита. Сумма платежа по кредиту в m-м месяце Ym определяется формулой
где S – общая сумма долга, подлежащая погашению [1]. Заметим, что формула (1) является приближенной, так как в ней используется приближенный пересчет годовой процентной ставки в месячную (R/12), в то же время ввиду своей выгодности для кредиторов именно эта формула наиболее часто используется на практике [1]. Нечеткие числа LR-типа – это разновидность нечетких чисел специального вида, задаваемых по определенным правилам [2, 3]. Функции принадлежности нечетких чисел LR-типа задаются с помощью невозрастающих четных неотрицательных действительных функций действительного аргумента L(x) и R(x), удовлетворяющих свойствам: 1) L(x)≥0, R(x)≥0; 2) L(–x)=L(x), R(–x)=R(x); 3) невозрастание на интервале (0,+∞); 4) L(0)=R(0)≤1. Пусть L(x) и R(x) – функции LR-типа. Функция принадлежности унимодального нечеткого числа А с модой а c помощью L(x) и R(x) задается следующим образом:
где а – мода; a>0, b>0 – левый и правый коэффициенты нечеткости. Таким образом, при заданных L(x) и R(x) нечеткое число LR-типа определяется тройкой (а, a, b). Пример функций L(x) и R(x):
где p – положительная константа. Текущие денежные поступления в m-м месяце от ИП заданы нечеткими числами LR-типа: Задан также индекс инфляции в m-м месяце в виде нечеткого числа LR-типа Определены функции L(x) и R(x). Длительность поступления средств от ИП – N, то есть Pm=0 при m>N. Требуется определить чистый приведенный доход ИП в нечетких условиях. Расчет чистого приведенного дохода Рассмотрим вначале случай, когда поступления от ИП и индекс инфляции в m-м месяце точно известны и определяются четкими числами Pm и Im. Формула для расчета чистого приведенного дохода имеет вид
где Коэффициент дисконтирования выбирается таким образом, чтобы привести стоимость к ценам на момент получения кредита, то есть чистый приведенный доход показывает поступления от ИП в ценах на момент получения кредита под ИП. Рассмотрим случай, когда текущие денежные поступления от ИП и индекс инфляции в m-м месяце заданы нечеткими числами LR-типа:
Формула для определения чистого приведенного дохода в данном случае имеет вид
Сначала определим значение коэффициента дисконтирования:
Для этого докажем утверждение о возведении нечеткого числа в целую положительную степень. Утверждение. Пусть
Доказательство. Согласно формуле умножения нечетких чисел LR-типа [2, 3] для нечетких чисел (m, a, b)LR×(n, g, d)LR=(mn, an+gm, bn+dm)LR. (6) Используя формулу (6), получим:
Предположив, что выражение (5) верно, будем иметь
С другой стороны, Таким образом, если верна формула (5), то верна и формула (8). Последнее утверждение совместно с формулой (7) на основе математической индукции доказывает правильность форму- лы (5) [4]. Утверждение доказано. Согласно формуле нахождения обратного нечеткого числа LR-типа для
Воспользовавшись формулами для определения степени нечеткого числа (5) и обратного для нечеткого числа (9), получим
Теперь перейдем к определению
Воспользовавшись формулой умножения нечетких чисел (10), получим
Подставляя формулу (10) в формулу (11), окончательно получим
где
Формула (12) позволяет рассчитать чистый приведенный доход, получаемый от инвестиционного проекта, использующего заемные средства, в случае, когда поступления от инвестиционного проекта и индекс инфляции заданы нечеткими числами LR-типа. Подытоживая, отметим, что в статье описан программный пакет «Анализ эффективности ИП с привлечением заемных средств». Получена расчетная формула, позволяющая определять чистый приведенный доход в нечетких условиях на основе арифметики нечетких чисел LR-типа. Для определения чистого приведенного дохода ИП в нечетких условиях можно использовать также комплексный или матричный метод выполнения операций над нечеткими числами LR-типа, что позволит упростить вычисления при использовании систем компьютерной математики [5]. Результаты исследования могут быть полезны в практике инвестиционного анализа. Литература 1. Четыркин Е.М. Финансовая математика. М.: Дело, 2000. 400 с. 2. Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях. Тюмень: Изд-во Тюменского гос. ун-та, 2000. 352 с. 3. Нечеткие множества в моделях управления и искусственного интеллекта; [под ред. Д.А. Поспелова]. М.: Наука, 1986. 312 c. 4. Курант Р., Роббинс Г. Что такое математика? М.: МЦНМО, 2001. 568 с. 5. Усков А.А., Киселев И.А. Комплексный и матричный методы выполнения арифметических операций над нечеткими числами // Управление большими системами. М.: ИПУ РАН, 2012. Вып. 40. С. 96–107. 6. Дюбуа Д., Прад А. Теория возможностей. Приложение к представлению знаний в информатике. М.: Радио и связь, 1990. 288 с. 7. Кучарина Е.А. Инвестиционный анализ. СПб: Питер, 2006. 160 с. 8. Непомнящий Е.Г. Инвестиционное проектирование. Таганрог: Изд-во ТРТУ, 2003. 262 с. 9. Пытьев Ю.П. Возможность. Элементы теории и применения. М.: ЭдиториаЛ. УРСС, 2000. 192 с. 10. Пытьев Ю.П. Возможность как альтернатива вероятности. Математические и эмпирические основы, применение. М.: Физматлит, 2007. 464 с. 11. Усков А.А., Кузьмин А.В. Интеллектуальные технологии управления. Искусственные нейронные сети и нечеткая логика. М.: Горячая Линия–Телеком, 2004. 143 с. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=3488 |
Версия для печати Выпуск в формате PDF (7.68Мб) Скачать обложку в формате PDF (1.35Мб) |
| Статья опубликована в выпуске журнала № 2 за 2013 год. [ на стр. 178-181 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Анализ систем обработки информации и управления с помощью групповых нечетких чисел
- Комплексная верификация результатов прогнозирования характеристик транспортной системы
- Диагностирование функциональной пригодности развивающихся многофункциональных автоматизированных систем на основе перестраиваемой модели
- Нечеткая многокритериальная система поддержки принятия решений DecernsFMCDA
- Анализ гибридных регуляторов в моделях управления техническими объектами в изменяющихся условиях
Назад, к списку статей



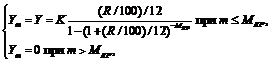 (1)
(1)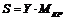 ,
,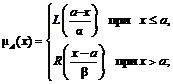
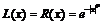 ,
, 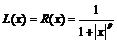 ,
,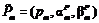 .
.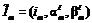 .
.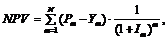 (2)
(2)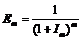 – коэффициент дисконтирования с учетом инфляции в m-м месяце.
– коэффициент дисконтирования с учетом инфляции в m-м месяце.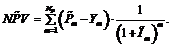 (3)
(3)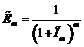 . (4)
. (4) – нечеткое число LR-типа, тогда при m>0 целая положительная степень n нечеткого числа
– нечеткое число LR-типа, тогда при m>0 целая положительная степень n нечеткого числа 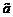 определяется формулой
определяется формулой . (5)
. (5)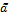 =(m, a, b)LR и
=(m, a, b)LR и 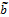 =(n, g, d)LR при m>0, n>0 можно записать:
=(n, g, d)LR при m>0, n>0 можно записать: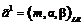
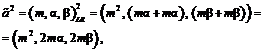
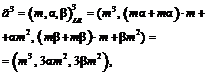 (7)
(7)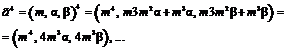
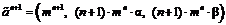 . (8)
. (8)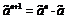 , используя формулы (5) и (6), также приходим к выражению (8).
, используя формулы (5) и (6), также приходим к выражению (8).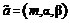 [3]
[3]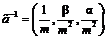 . (9)
. (9)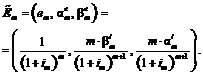 (10)
(10)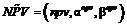 .
.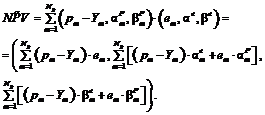 (11)
(11)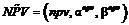 , (12)
, (12)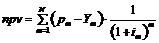 ,
,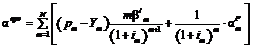 ,
,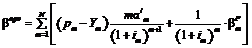 .
.