Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Решение краевых задач математической физики на радиально-базисных нейронных сетях
Аннотация:
Abstract:
| Авторы: Артюхина Е.В. () - , Горбаченко В.И. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 11716 |
Версия для печати Выпуск в формате PDF (2.31Мб) |
Методы решения дифференциальных уравнений в частных производных (ДУЧП) с применением радиально-базисных функций (RBF) вызывают большой интерес (см.: http://uahtitan.uah.edu/kansaweb.html). Эти методы могут быть эффективно реализованы на радиально-базисных нейронных сетях (RBFNN) (см.: А.Н. Васильев, Д.А. Тархов. Новые подходы на основе RBF-сетей к решению краевых задач для уравнения Лапласа на плоскости. // Нейрокомпьютеры: разработка, применение. 2004. № 7-8). RBF-сеть рассматривают как аппроксиматор неизвестной функции решения:
Для создания оптимальной сети можно использовать различные виды RBF, наиболее часто используемыми являются мультиквадрик Рассмотрим работу RBFNN при решении ДУЧП. На вход сети подаются координаты точек области (точек коллокации) В работе Е.В. Яничкиной и В.И. Горбаченко «Решение эллиптических дифференциальных уравнений в частных производных с использованием радиально-базисных нейронных сетей» (М.: МИФИ. 2006) рассмотрен подход к обучению нейронной сети, где радиально-базисная сеть явным образом аппроксимирует производные функции
Для нахождения решения определяется функционал ошибки как сумма квадратов невязок, получаемых при подстановке u и производных в уравнение и в граничные условия. Предлагается другой подход к обучению, использующий конечно-разностную аппроксимацию уравнения. При этом отпадает необходимость расчета явным образом частных производных. Функционал ошибки определяется как сумма квадратов невязок, получаемых при подстановке u в конечно-разностную аппроксимацию во внутренних и граничных точках. Как в первом, так и во втором подходе для обучения сети используется градиентный алгоритм обучения, минимизирующий функционал ошибки I путем настройки весов w, центров c и ширины a.
где В качестве модельной задачи с целью сравнительного анализа было взято уравнение Пуассона
с граничными условиями Дирихле по всей границе области
что позволяет использовать ее для сравнительного анализа. Задача имеет аналитическое решение
которое использовалось для оценки точности решения. Рассмотрим градиентный алгоритм обучения RBFNN при решении задачи –. Конечно-разностная аппроксимация имеет вид:
Функционал ошибки равен:
где Обозначим через
а также введем следующие обозначения:
Функционал ошибки равен:
Несложно вычисляются градиенты функционала по параметрам сети. Прежде всего исследовалось решение контрольной задачи при фиксированном наборе контрольных точек и фиксированных (подбираемых) коэффициентах скорости обучения. Первоначально центры располагаются в узлах заданной сетки. Начальные значения весов принимаются нулевыми. Процесс обучения продолжается до достижения функционалом ошибки заданной величины. Предусмотрен также выход из цикла обучения по достижении предельного числа циклов обучения. В программе также рассчитывается относительная среднеквадратическая погрешность решения
где В процессе решения выводятся графики зависимостей функционала ошибки и относительной среднеквадратической погрешности решения от номера цикла обучения, а также графики погрешности решения по сравнению с аналитическим решением и расположение центров в процессе решения. Эксперименты показали трудность подбора фиксированных скоростей обучения. При этом на скорость обучения сети основное влияние оказывает скорость обучения весов. При больших значениях скорости обучения процесс обучения носит колебательный характер и расходится. При малых значениях скорости достигается большая точность, но обучение производится очень медленно. При постоянных скоростях существует минимум функционала ошибки, после которого функционал начинает расти. Причем с уменьшением скорости обучения весов график становится более гладким и достигается большая точность, но ценой большего числа итераций. В целом процесс обучения весьма медленный и при каждом значении скорости обучения наблюдается предельное достигаемое значение функционала ошибки. Предлагается подход, основанный на алгоритме градиентного спуска и вычислении в каждом цикле обучения коэффициента скорости обучения. Градиентный алгоритм обучения для весов:
при зафиксированных центрах и ширине подставим в . Обозначим
Тогда
Выберем скорость обучения
Несмотря на несколько громоздкий вид, коэффициент скорости обучения В целях борьбы с переобучением сети целесообразно применить случайное изменение контрольных точек в процессе обучения сети. Необходимо также исследовать вычисляемые в процессе обучения коэффициенты скорости обучения весов сети. Исследовалось решение задачи со случайным выбором контрольных точек, с постоянными скоростями обучения. Чтобы обеспечить случайный набор контрольных точек, расположенных на сетке Задача решалась при следующих исходных данных: В процессе решения получены следующие результаты: за 724 итерации достигнуто значение функционала ошибки I=1.4958e-005. Средняя относительная погрешность на сетке 0.0135. При случайном выборе контрольных точек переобучение не проявляется. График погрешности по сравнению с аналитическим решением (см.: Numerical solution of elliptic partial differential equation using radial basis function neural networks / L. Jianyu, L. Siwei, Q. Yingjiana, H. Yapinga // Neural Networks. – 2003. – 16(5/6)) показывает лучший результат. Исследование алгоритма со случайным набором контрольных точек и вычисляемым коэффициентом скорости обучения весов в алгоритме градиентного спуска дало следующие результаты: за 179 итераций достигнуто значение функционала ошибки I=2.7929e-007, средняя относительная погрешность на сетке 0.0071. Эффект от применения вычисляемого коэффициента заключается не столько в сокращении числа циклов обучения, сколько в упрощении вычислений. График изменения коэффициента скорости обучения весов носит колебательный характер (см. рис.). Погрешность по сравнению с аналитическим решением несколько меньше, чем в других вариантах, и не превышает 0,00021. Экспериментально доказана эффективность предложенного варианта алгоритма градиентного спуска обучения RBF‑сети, отличающегося от известных алгоритмов использованием конечно-разностной аппроксимации дифференциального уравнения и вычисляемым коэффициентом скорости обучения весов сети. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=354 |
Версия для печати Выпуск в формате PDF (2.31Мб) |
| Статья опубликована в выпуске журнала № 3 за 2007 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Компьютерная технология проектирования перестраиваемых нерекурсивных фильтров
- Методы поисковой адаптации на основе механизмов генетики, самообучения и самоорганизации
- Кросс-система автоматизации разработки программного обеспечения на базе языка высокого уровня Рада
- Информационная система управления деятельностью персонала
- Информационные системы по оценке и анализу инвестиционных проектов малого бизнеса
Назад, к списку статей



 .
.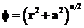 ,
,  , и гауссиан
, и гауссиан  , где
, где 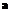 – определенная пользователем константа.
– определенная пользователем константа.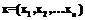 , n –размерность пространства. Радиальная функция каждого нейрона характеризуется своими параметрами: центром
, n –размерность пространства. Радиальная функция каждого нейрона характеризуется своими параметрами: центром 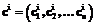 и шириной
и шириной 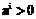 , которые уточняются в процессе обучения. Каждый нейрон радиально-базисного слоя выполняет нелинейное преобразование
, которые уточняются в процессе обучения. Каждый нейрон радиально-базисного слоя выполняет нелинейное преобразование 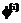 , аргументом которого является расстояние от точки
, аргументом которого является расстояние от точки 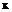 до соответствующего центра
до соответствующего центра 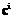 . Роль выходного слоя сводится к взвешенному суммированию сигналов, поступающих от нейронов скрытого слоя
. Роль выходного слоя сводится к взвешенному суммированию сигналов, поступающих от нейронов скрытого слоя 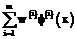 . На выходе получаем значение искомой функции в точке x:
. На выходе получаем значение искомой функции в точке x: 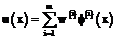 . Обучение сети сводится к нахождению неизвестных параметров: весов w, ширины a, центров c.
. Обучение сети сводится к нахождению неизвестных параметров: весов w, ширины a, центров c. . Из производные функции
. Из производные функции 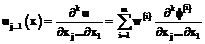 .
.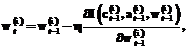
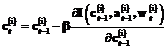 ,
,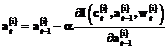 ,
,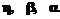 – скорости (коэффициенты) обучения. Процесс уточнения параметров продолжается до достижения определенной погрешности.
– скорости (коэффициенты) обучения. Процесс уточнения параметров продолжается до достижения определенной погрешности.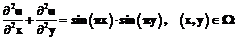
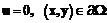 ,
, ,
,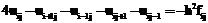 .
.
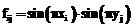 – функция правой части уравнения ;
– функция правой части уравнения ; 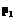 – значение граничных условий первого рода в точке l границы;
– значение граничных условий первого рода в точке l границы;  и K – количество внутренних и граничных контрольных точек.
и K – количество внутренних и граничных контрольных точек.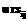 удовлетворение разностной схеме в точке (xi,yj):
удовлетворение разностной схеме в точке (xi,yj):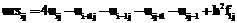 ,
, ,
, 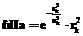 ,
,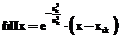 ,
, 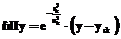 .
.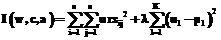 .
.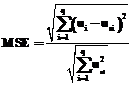 ,
, – аналитическое решение в точке I; q – число внутренних и граничных контрольных точек.
– аналитическое решение в точке I; q – число внутренних и граничных контрольных точек.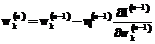 ,
,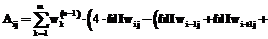
 ,
,
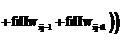 ,
,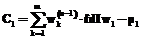 ,
,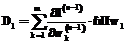 .
. .
.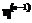 из условия минимума функционала
из условия минимума функционала 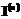 при заданном значении
при заданном значении 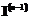 , получаем
, получаем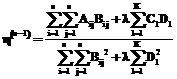 .
. , случайно задается число n.
, случайно задается число n. 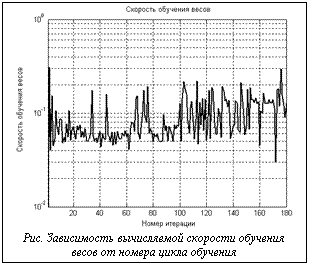 Решение при случайно выбранных контрольных точках повторяется некоторое число раз (внутренние итерации). Первоначально центры нейронов располагались внутри и вне области решения на регулярной сетке.
Решение при случайно выбранных контрольных точках повторяется некоторое число раз (внутренние итерации). Первоначально центры нейронов располагались внутри и вне области решения на регулярной сетке.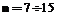 – количество узлов на стороне сетки контрольных точек;
– количество узлов на стороне сетки контрольных точек; 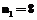 – количество узлов на стороне сетки центров нейронов. Скорости обучения:
– количество узлов на стороне сетки центров нейронов. Скорости обучения: 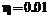 ,
, 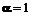 ,
, 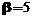 .
.