Journal influence
Bookmark
Next issue
Application of the fuzzy sets theory to the decision making problem under conditions of uncertainty
The article was published in issue no. № 3, 2013 [ pp. 28-31 ]Abstract:The paper presents an approach to decision making under conditions of uncertainty, based on the application of fuzzy sets theory methods. This approach is applied for decision making problems, which are formally presented in terms of the game theory (statistical games). The task must be represented in the form of decision matrix, indicating the set of all pos-sible alternatives, the set of possible states of the system, the values of performance indicators, as well as the states probabil-ity distribution. This approach is an alternative to thewell-known decision criteria used in statistical games problems, such as Bayesian criterion, the probability maximization, dispersion minimum, modal criteria, etc. The distinctive feature of this ap-proach is that the expert doesn’t need the exact numerical values as the efficiency values, but he can specify some verbal de-scriptions in the form of sentences. This is achieved by using fuzzy sets with their membership functions as the assessment of functionality. Using methods of the fuzzy sets theory allows simplifying the expert evaluation process and increasing the de-cision making quality.
Аннотация:Описан подход к принятию решений в условиях неопределенности, основанный на методах теории нечетких множеств и предназначенный для применения в задачах принятия решений, которые формально представляются в терминах теории игр, а именно статистических игр. При этом задача должна быть представлена в форме матрицы решений с указанием множеств всех возможных альтернатив ивозможных состояний рассматриваемой системы, значений показателя эффективности, а также распределения вероятностей состояний системы. Данный подход явля-ется альтернативой известным критериям принятия решений, используемым в задачах статистических игр, таким, как критерий Байеса, критерии максимизации вероятности и минимума дисперсии, модальный критерий и др. Отли-чительной особенностью рассматриваемого подхода является то, что при формировании матрицы решений эксперт может указывать не точные численные значения показателя эффективности, а словесные описания в виде фраз на ес-тественном языке. Это достигается за счет использованияв качестве значений оценочного функционала нечетких множеств со своими функциями принадлежности. Введениеметодов теории нечетких множеств позволяет упростить процесс экспертной оценки и улучшить качество принимаемых решений.
| Authors: Pogorelov A.S. ( pogorelov-alserg@yandex.ru) - Don Branch of the Space Simulator Center (Engineer-Programmer), Novocherkassk, Russia, Panfilov A.N. (panfiloff@rambler.ru) - South-Russian State Polytechnical University (Associate Professor), Novocherkassk, Russia, Ph.D | |
| Keywords: decision matrix, expert methods, uncertainty, statistical games, fuzzy sets theory, decision theory |
|
| Page views: 12877 |
Print version Full issue in PDF (13.63Mb) Download the cover in PDF (1.39Мб) |
Принятие решений – это процесс выбора из множества альтернативных вариантов действий одного или нескольких, оптимальных по какому-либо критерию. Данная проблема присутствует в самых различных областях деятельности. При этом окончательное решение всегда остается за человеком. Однако современное состояние науки и техники позволяет создавать средства поддержки принятия решений, способные значительно облегчить для ЛПР выбор оптимальной альтернативы действий. Существует достаточно обширный математический аппарат теории принятия решений (ТПР), который включает множество методов и технологий поддержки деятельности ЛПР. Одним из методов является теория игр, относящаяся к разделу ТПР, посвященному принятию решений в условиях неопределенности. Теория игр описывает ситуации противостояния двух и более сторон; каждая из них имеет свою стратегию и нацелена на получение максимального выигрыша. При этом различают статистические игры, где противником ЛПР выступает природа, действия которой не имеют осознанного характера [1]. В такой ситуации задачу принятия решений можно описать так, как показано в таблице 1. Таблица 1 Матрица решений
Модель задачи принятия решений включает следующие элементы: – множество всех возможных вариантов действий (альтернатив) D={d1, d2, …, dn}; – множество всех возможных состояний рассматриваемой системы S={s1, s2, …, sm}; – оценочный функционал (показатель эффективности) F={fij}, i=1, ..., n, j=1, …, m, который определяет степень эффективности принимаемого решения di при условии, что рассматриваемая система окажется в состоянии sj. Элементы матрицы решений – значения оценочного функционала fij – задаются при помощи экспертных методов. То есть предполагается, что эксперт на основании своего опыта и знаний предметной области способен количественно оценить степень эффективности принимаемых решений в зависимости от состояний рассматриваемой системы. Кроме этого, могут быть известны вероятности каждого состояния рассматриваемой системы. Тогда к элементам модели задачи принятия решений добавляется еще один элемент – вектор распределения вероятностей состояний системы P={p1, p2, …, pm}, где элемент pi определяет вероятность нахождения рассматриваемой системы в состоянии si. Таким образом, модель задачи принятия решений может быть представлена кортежем . (1) Для описанной модели задачи принятия решений известен ряд критериев оптимальности: критерии Байеса, максимизации вероятности, минимума дисперсии, модальный критерий и др. Каждый из них описывает функцию W(F, P), которая достигает экстремума при определенном значении fopt, соответствующем оптимальной стратегии dopt. Между собой данные критерии различаются видом функции W(F, P). Существенный недостаток использования описанных критериев оптимальности в том, что эксперту при формировании матрицы решений приходится указывать точное значение оценочного функционала fij, а это зачастую является нетривиальной задачей, так как область определения показателя эффективности может быть очень большой и выбрать одно конкретное значение непросто даже для достаточно опытного, знающего предметную область специалиста. Рассмотрим задачу принятия решений (1), но в качестве оценки показателя эффективности эксперт может указывать не точное количественное значение, а качественное, словесное описание показателя эффективности. Данный подход можно наглядно продемонстрировать на примере задачи выбора технологии обработки данных в информационных системах (ИС) [2]. Для некоторой ИС можно выбрать одну из трех технологий обработки данных. В каждый момент времени ИС характеризуется количеством пользователей, обращающихся к ней, и интенсивностью запросов. В определенный момент возможны следующие состояния ИС: s1 – количество пользователей небольшое и интенсивность за- просов низкая; s2 – количество пользователей большое, но интенсивность запросов низкая; s3 – количество пользователей небольшое, но интенсивность запросов высокая; s4 – количество пользователей большое и интенсивность запросов высокая. В описанных условиях возможен выбор из трех технологий обработки данных: d1 – технология 1, d2 – технология 2, d3 – технология 3. Кроме этого, согласно собранной статистике, известна вероятность каждого из состояний ИС: p1 – вероятность состояния s1, p2 – вероятность состояния s2, p3 – вероятность состояния s3, p4 – вероятность состояния s4. В качестве показателя эффективности выступает время реакции ИС на запросы пользователя. При этом для оценки показателя эффективности при формировании матрицы решений эксперт может выбрать одно из следующих словесных выражений: «малое время реакции», «время реакции ниже среднего», «время реакции среднее», «время реакции выше среднего» или «время реакции большое». Задача состоит в том, чтобы выбрать технологию обработки данных, при которой время реакции будет минимальным с учетом вероятности состояний ИС. Предположим, что в результате выбора одной из альтернатив время реакции ИС не будет превышать 10 секунд. Другими словами, область определения показателя эффективности лежит в интервале [0, 10]. Тогда словесные выражения «малое время реакции», «время реакции ниже среднего», «время реакции среднее», «время реакции выше среднего» и «время реакции большое» можно представить нечеткими множествами T1, T2, T3, T4 и T5 соответственно. Допустим, что функции принадлежности этих нечетких множеств имеют вид, представленный на рисунке 1. Пусть экспертами в данной предметной области была составлена матрица решений, представленная в таблице 2. Таблица 2 Матрица решений для задачи выбора технологии обработки данных
Для выбора оптимального решения каждой альтернативе поставим в соответствие некий обобщенный показатель Fi*, характеризующий эффективность принятия решения di. Другими
Учесть вероятность состояния можно следующим образом. Отсечем функции принадлежности горизонтальными линиями в соответствии с текущим распределением вероятностей и получим видоизмененные нечеткие множества, представленные на рисунке 3.
Затем произведем операцию агрегирования над видоизмененными нечеткими множествами и получим обобщенный показатель, учитывающий текущее распределение вероятностей состояний. Функция принадлежности агрегированного показателя изображена на рисунке 4. Численное значение обобщенного показателя для альтернативы d1 можно получить, выполнив процедуру дефаззификации нечеткого множест- ва F1*. Аналогично опре Общий алгоритм предлагаемого подхода состоит из следующих шагов. 1. Представить задачу в виде (1). Для этого необходимо – построить множество всех допустимых решений D; – построить множество всех возможных состояний рассматриваемой системы S; – выбрать показатель эффективности F и построить множество его значений, каждое из которых описывается определенным нечетким множеством; – заполнить матрицу решений, представленную в таблице 1, значениями показателя эффективности; – определить вектор вероятностей состояний системы P. 2. Для каждой строки матрицы решений di определить численное значение агрегированного показателя a(Fi*), i=1, ..., n. Для этого необходимо выполнить следующие действия: – для каждого состояния системы sj отсечь функцию принадлежности показателя эффективности fij с учетом соответствующего значения вероятности pj; при этом функция принадлежности показателя эффективности f /ij запишется в виде
– с помощью операции объединения нечетких множеств определить агрегированный показатель эффективности – с помощью процедуры дефаззификации нечеткого множества Fi* определить численное значение показателя эффективности a(Fi*); существует множество методов дефаззификации нечетких множеств, например, метод по среднему центру, метод по сумме центров, метод центра тяжести и др. [3]. 3. Если условие задачи требует максимизи- ровать показатель эффективности F, то в качест- ве оптимального решения выбрать альтернативу с максимальным численным значением a(Fi*); если необходимо минимизировать, то с минималь- ным. Представленный подход, который является развитием идей, изложенных в работе [4], предназначен для применения в задачах принятия решений и использует аппарат теории нечетких множеств для построения агрегированного показателя эффективности альтернатив. Данный подход удобнее других известных методов принятия решений благодаря использованию замены количественных значений показателя эффективности на качественные, словесные описания, которыми удобнее оперировать человеку. Литература 1. Черноморов Г.А. Теория принятия решений: учеб. пособие. Новочеркасск: Изд-во ЮРГТУ, 2002. 276 с. 2. Панфилов А.Н., Черноморов Г.А., Скоба А.Н. Математическая модель процессов автоматизированной обработки информации при внедрении интегрированных информационных систем на предприятиях // Изв. вузов. Электромеханика. 2001. № 1. С. 77–80. 3. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы; [пер. с польск. И.Д. Рудинского]. М.: Горячая линия–Телеком, 2006. 452 с. 4. Панфилов А.Н., Погорелов А.С. Модель принятия решений на основе нечеткой информации // Моделирование. Теория, методы и средства: матер. XIII Междунар. науч.-практич. конф. (27 февраля 2013 г., Новочеркасск). Новочеркасск: ЮРГТУ(НПИ), 2013. С. 59–62. References 1. Chernomorov G.A., Teoriya prinyatiya resheny: ucheb. posobie [Decision making theory: study guide], Novocherkassk, SRSTU publ., 2002. 2. Panfilov A.N., Chernomorov G.A., Skoba A.N., Izv. vuzov. Elektromekhanika [News of higher educational institutions. Electromechanics], 2001, no. 1, pp. 77–80. 3. Rutkovskaya D., Pilinsky M., Rutkovsky L., Neyronnye seti, geneticheskie algoritmy i nechetkie sistemy [Neural network, genetic algorithms and fuzzy systems], Moscow, Goryachaya liniya – Telekom, 2006. 4. Panfilov A.N., Pogorelov A.S., Modelirovanie. Teoriya, metody i sredstva: materialy XIII Mezhdunar. nauch.-prakt. konf. [Modeling. Theory, methods and tools: proc. of XIII int. research-to-practice conf.], Novocherkassk, SRSTU, 2013, pp. 59–62. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Permanent link: http://swsys.ru/index.php?page=article&id=3554&lang=en |
Print version Full issue in PDF (13.63Mb) Download the cover in PDF (1.39Мб) |
| The article was published in issue no. № 3, 2013 [ pp. 28-31 ] |
Perhaps, you might be interested in the following articles of similar topics:
- Подход к использованию меры возможности при оценке принимаемых решений
- Информационная система анкетирования «Апофаси»
- Использование формулы Байеса при оценивании выполнения практик модели CMMI®
- Выбор критериев принятия решений в организационно-технических системах с использованием информационных ситуаций
- Об использовании аппарата теории принятия решений в задачах оценивания согласно модели CMMI®
Back to the list of articles
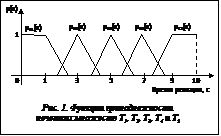 словами, показатель Fi* отражает ожидаемое время реакции системы при условии, что вероятности возможных состояний ИС распределены, как представлено в таблице 2. В соответствии с постановкой задачи альтернатива, показатель Fi* которой окажется минимальным, и будет оптимальной. Очевидно, что показатель Fi* должен описываться нечетким множеством, которое получается в результате агрегирования нечетких множеств – значений оценочного функционала для альтернативы di. Так, например, для альтернативы d1 показатель F1* будет комбинацией нечетких множеств T1, T2, T4 и T5. В качестве операции для агрегирования выберем операцию объединения нечетких множеств. Тогда функция принадлежности агрегированного показателя F1* примет вид, представленный на рисунке 2.
словами, показатель Fi* отражает ожидаемое время реакции системы при условии, что вероятности возможных состояний ИС распределены, как представлено в таблице 2. В соответствии с постановкой задачи альтернатива, показатель Fi* которой окажется минимальным, и будет оптимальной. Очевидно, что показатель Fi* должен описываться нечетким множеством, которое получается в результате агрегирования нечетких множеств – значений оценочного функционала для альтернативы di. Так, например, для альтернативы d1 показатель F1* будет комбинацией нечетких множеств T1, T2, T4 и T5. В качестве операции для агрегирования выберем операцию объединения нечетких множеств. Тогда функция принадлежности агрегированного показателя F1* примет вид, представленный на рисунке 2.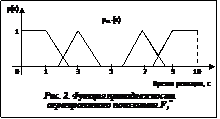 Нечеткое множество на этом рисунке описывает комбинацию значений показателя эффективности для альтернативы d1, но не учитывает, что состояния, которым соответствуют эти значения, могут возникать с различной вероятностью. Другими словами, изменение распределения вероятностей состояний должно приводить к изменению обобщенного показателя.
Нечеткое множество на этом рисунке описывает комбинацию значений показателя эффективности для альтернативы d1, но не учитывает, что состояния, которым соответствуют эти значения, могут возникать с различной вероятностью. Другими словами, изменение распределения вероятностей состояний должно приводить к изменению обобщенного показателя. Таким образом, функцию принадлежности нечеткого множества T1 отсекли по вероятности p1=0,1 (в соответствии с таблицей 2), функцию принадлежности для T2 – по вероятности p2=0,2, функцию принадлежности для T4 – по вероятности p3=0,6 и функцию принадлежности для T5 – по вероятности p4=0,1.
Таким образом, функцию принадлежности нечеткого множества T1 отсекли по вероятности p1=0,1 (в соответствии с таблицей 2), функцию принадлежности для T2 – по вероятности p2=0,2, функцию принадлежности для T4 – по вероятности p3=0,6 и функцию принадлежности для T5 – по вероятности p4=0,1.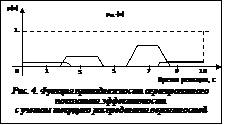 деляются численные значения обобщенного показателя для остальных альтернатив. Та альтернатива, для которой численное значение показателя эффективности окажется минимальным, и будет оптимальным решением поставленной задачи.
деляются численные значения обобщенного показателя для остальных альтернатив. Та альтернатива, для которой численное значение показателя эффективности окажется минимальным, и будет оптимальным решением поставленной задачи.
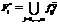 ;
;