Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Программа для решения задачи об оптимальной переориентации шара
Аннотация:Рассматривается задача оптимального качения шара по плоскости с прокручиванием, но без проскальзывания, являющаяся модификацией одной известной модельной задачи геометрической механики, в которой требуется оптимально перевести шар из начального состояния в конечное без прокручивания и проскальзывания. Обе проблемы остаются открытыми, а в случае качения без прокручивания до сих пор неизвестны оптимальные траектории даже в подзадаче о переориентации, когда шар требуется вернуть в исходную точку с новой ориентацией. Если же разрешить шару прокручиваться, задача значительно упрощается.В данной работе описан программный интерфейс для решения задачи об оптимальной переориентации шара с прокручиванием. С использованием необходимых признаков оптимальности экстремальных траекторий, полученных ранее, разработан алгоритм решения, реализованный в виде программного интерфейса в среде Wolfram Mathematica. Разработанная программа позволяет построить и изучить оптимальное возвращение шара. Рассмотренный в статье алгоритм можно использовать для планирования пути сферического робота.
Abstract:The article considers the optimal problem of a rolling ball on a plane with twisting but without slipping. It is a modification of a classical model problem from geometric mechanics, when it is required to optimally transfer the ballfrom a given initial state to a terminal one without twistingor slipping. Nowadays both problems are open and even in the non-twisting case the optimal trajectories in the reorientation sub-problem are unknown (when it is required to transfer the ball to the initial point with a new orientation). But if twisting is allowed, the problem becomes significantly simplier. The paper considers the program interface for optimal reorientation in the twisting case. Using some necessary optimality conditions obtained in [10] we construct a solution algorithm, whichwas realized as a program interface in Wolfram Mathematica.The algorithm considered in this paper can be used for motion planing of a spherical robot.
| Авторы: Бесчастный И.Ю. (i.beschastnyi@gmail.com) - Институт программных систем им. А.К. Айламазяна РАН (аспирант), г. Переславль-Залесский, Россия | |
| Ключевые слова: качение поверхностей., механика, mathematica, моделирование, программный интерфейс |
|
| Keywords: rolling surfaces, mechanics, mathematica, modeling, program interface |
|
| Количество просмотров: 7689 |
Версия для печати Выпуск в формате PDF (13.63Мб) Скачать обложку в формате PDF (1.39Мб) |
Рассмотрим механическую систему, состоящую из шара, который катится по горизонтальной плоскости без проскальзывания, но с прокручиванием. Состояние такой системы описывается координатами точки контакта шара и плоскости и матрицей ориентации шара. В задаче о переориентации требуется перекатить шар из одной ориентации в другую так, чтобы достигался минимум вращательной энергии, а координаты точек контакта в начальном и конечном состояниях совпадали. В статье описаны алгоритм решения этой задачи и программный интерфейс, позволяющий изучить качение шара. Впервые задача об оптимальном качении шара по плоскости была поставлена Дж. Хаммерсли [1] и впоследствии исследовалась различными авторами [2–4]. В своей работе Хаммерсли рассматривал качение по плоскости без проскальзывания и прокручивания из произвольного начального состояния в произвольное конечное. Эта задача до сих пор не решена, что связано со сложной структурой экстремальных траекторий (проекции экстремальных траекторий на плоскость – эластики Эйлера, а матрица ориентации выражается через эллиптические функции Якоби и эллиптический интеграл третьего рода [3]). При качении с прокручиванием экстремальные траектории выражаются в элементарных функциях, что существенно облегчает исследование оптимальности. В этом случае шар катится лишь по прямым и синусоидам. Данная задача имеет приложения в механике и робототехнике и представляет собой хорошую модельную задачу в субримановой геометрии [5, 6]. В настоящее время существует большой интерес к созданию роботов, обладающих большей проходимостью, чем колесные. Одной из альтернатив колесным роботам являются сферические роботы. Благодаря своей конструкции они значительно лучше колесных машин справляются с лестницами и прочими препятствиями. Эти роботы могут быть герметичными, что позволяет им передвигаться по снегу и даже по воде. В основе их конструкции могут лежать различные принципы: например, изменение положения центра тяжести, использование колесных механизмов, деформация и т.д. [7]. Описанный в статье алгоритм может использоваться для планирования пути сферических роботов, управляемых тремя роторами внутри. При такой конструкции можно добиться прокручивания. Реальные прототипы подобных машин описываются, например, в [7–9]. Особенность планирования пути сферических роботов заключается в том, что нужно перевести шар в новую точку на плоскости с заданной ориентацией. Это позволяет использовать неподвижную, закрепленную внутри оболочки робота камеру, в результате чего количество сервоприводов в конструкции сравнимо с количеством сервоприводов, используемых в автономных колесных роботах. Постановка задачи и необходимые сведения. Закрепим в трехмерном пространстве неподвижный репер (e1, e2, e3) так, чтобы горизонтальная плоскость, по которой катится шар, была натянута на орты (e1, e2), а орт e3 направлен в верхнее полупространство. Выберем подвижный репер Выберем в качестве управления компоненты единичного вектора угловой скорости
(x, y)Î (x(0), y(0), R(0))=(0, 0, Id), (x(t1), y(t1), R(t1))=(0, 0, R1),
где t1 фиксированное. Приведем вначале общее описание экстремальных траекторий в задаче об оптимальном качении шара с прокручиванием. Исходим из того, что при оптимальном движении вектор угловой скорости
где
где В дальнейшем вместо матрицы поворота R будет удобно использовать соответствующий ей единичный кватернион q=q0+iq1+jq2+kq3,
Это позволяет переписать уравнение (2) в кватернионном виде:
Из двух кватернионов ±q, соответствующих матрице R, здесь приведен кватернион с начальными условиями q=1. Теперь перейдем от общей задачи управления шаром к подзадаче о переориентации. Опираемся на утверждения, доказанные в [10]: 1) шар может вернуться назад в начало координат только в случае, если он катится по отрезку или стоит на месте и крутится; 2) вращение на месте будет оптимальным, если шар повернется на угол a≤π вокруг вертикальной оси; 3) при качении по отрезку вектор угловой скорости 4) при качении по отрезку шар вернется в начало координат в момент времени
5) качение по отрезку неоптимально, если
Положим, что
Тогда в момент первого возвращения ориентация шара будет иметь вид
Если q1¹0, данная система имеет единственное решение (α, γ), удовлетворяющее условиям в (5), и по этому решению единственным образом могут быть найдены значения (ω, ψ0). Алгоритм решения задачи. На основе теоретических результатов автором построен алгоритм решения задачи об оптимальной переориентации и написана программа, наглядно демонстрирующая оптимальное качение шара. Блок-схема алгоритма приведена на рисунке 1. На первом шаге определяется конечная ориентация шара с помощью угла вращения q и оси вращения, заданной вектором (x, y, z). Если ось вращения вертикальна, оптимальным является кручение на месте (блоки 3–10). При этом шар должен повернуться на угол, меньший π, как указано ранее. По этой причине оптимальным будет вращение либо на угол q (блоки 7, 9), либо на угол 2π–q (блоки 6, 8). Если же вектор x¹0, y¹0, оптимальным должно быть качение по отрезку (блоки 11–19). В этом случае сначала по оси вращения и углу строится соответствующая пара кватернионов q±=±(q0+iq1+ +jq2+kq3), затем каждый кватернион поворачивается на угол b±, который определяется из соотношений
Тогда конечная ориентация будет задаваться кватернионами Далее решаются две системы (6):
Для решения этой системы использовался метод Ньютона с выбором начального значения по равномерной сетке. Вычислительные эксперименты показали, что для нахождения корня достаточно сетки из девяти узлов. Для каждой пары полученных значений (a±, g±) с помощью (5) получаются соответствующие величины Описание программного интерфейса. Алгоритм решения задачи о переориентации шара был реализован в среде Mathematica. Программный интерфейс показан на рисунке 2. В левой части находится панель управления, которая позволяет ввести входные данные и управлять элементами интерфейса. В правой части отображается оптимальное качение шара. Входные данные (координаты оси и угла вращения) задаются с помощью ползунков X, Y, Z и Angle. Панель Run the animation позволяет запускать/останавливать анимацию, изменять ее скорость и переходить к конкретному моменту времени с помощью ползунка Time. С помощью панели Customize можно управлять следующими элементами отображения качения: – Sphere’s opacity – прозрачность сферы; – Planes’s opacity – прозрачность плоскости; – Meredians – показать/скрыть меридианы на сфере; – Movingframe – показать/скрыть подвижный репер; – StationaryFrame – показать/скрыть неподвижный репер; – ResultFrame – показать/скрыть конечный репер; – ResultFrameRGB – отображать конечный репер в цвете; – PlaneGrid – показать/скрыть координатную сеть на плоскости; – PlaneCurve – показать/скрыть траекторию точки контакта на плоскости; – SphereCurve – показать/скрыть траекторию точки контакта на сфере. Для решения системы (6) в программе использовался метод Ньютона с выбором начального значения по сетке в области изменения (α, γ), указанной в (5). В заключение отмет Полученные результаты могут использоваться для планирования пути и управления колесными роботами с роторами. Автор благодарен С. Попову за любезно предоставленные материалы для написания данной статьи. Литература 1. Hammersley J.M., Oxford commemoration ball. Probability, Statistics and Analysis, Cambridge Univ. Press, 1983, pp. 112–142. 2. Arthurs A.M., Walsh G.R., On Hammersley’s minimum problem for a rolling sphere, Math. Proc. Cambridge Phil. Soc., 1986, Vol. 99, pp. 529–534. 3. Jurdjevic V., The geometry of the plate-ball problem, Arch. Rat. Mech. Anal., 1993, Vol. 124, pp. 305–328. 4. Маштаков А.П., Сачков Ю.Л. Экстремальные траектории и точки Максвелла в задаче об оптимальном качении сферы по плоскости // Матем. сб., 2011. Т. 202 (9). С. 97–120. 5. Аграчев А.А., Сачков Ю.Л. Геометрическая теория управления. М.: Физматлит, 2005. 392 с. 6. Montgomery R., A Tour of Subriemannian Geometries, Their Geodesies and Applications. American Mathematical Society, 2006, 259 с. 7. Chase R., Pandya A., A review of Active Mechanical Driving Principles of Spherical Robots. Robotics, 2012, Vol. 1, pp. 3–23. 8. Joshi V., Banavar R., Hippalgaonkar R., Design, modeling and controllability of a spherical mobile robot. Proc. 13th Nation. Conf. on Mech. and Machines, 2007, pp. 3–8. 9. Svinin M., Morinaga A., Yamamoto M., An analysis of the motion planning problem for a spherical rolling robot driven by internal rotors, IEEE/RSJ Intern. Conf. on Intell. Robots and Systems, 2012, pp. 414–419. 10. Бесчастный И.Ю. Об оптимальном назначении сферы по плоскости с прокручиванием, без проскальзывания // Математический сб. 2013. Т. 204 (10). References 1. Hammersley J.M., Probability, Statistics and Analysis, Cambridge Unv. Press, 1983, pp. 112–142. 2. Arthurs A.M., Walsh G.R., Math. Proc. Cambridge Phil. Soc., Vol. 99, 1986, pp. 529–534. 3. Jurdjevic V., Arch. Rat. Mech. Anal., Vol. 124, 1993, pp. 305–328. 4. Mashtakov A.P., Sachkov Yu.L., Matematicheskiy sbornik, Vol. 202 (9), 2011, pp. 97–120. 5. Agrachev А.А., Sachkov Yu.L., Control theory from the geometric point of view, Springer, 2004. 6. Montgomery R., A Tour of Subriemannian Geometries, Their Geodesies and Applications, American Mathematical Society, 2006. 7. Chase R., Pandya A., Robotics, Vol. 1, 2012, pp. 3–23. 8. Joshi V., Banavar R., Hippalgaonkar R., 13th National Conf. on Mechanics and Machines, 2007, pp. 3–8. 9. Svinin M., Morinaga A., Yamamoto M., IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, 2012, pp. 414–419. 10. Beschastny I.Yu., Matematicheskii Sbornik, 2013, Vol. 204 (10). |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=3598 |
Версия для печати Выпуск в формате PDF (13.63Мб) Скачать обложку в формате PDF (1.39Мб) |
| Статья опубликована в выпуске журнала № 3 за 2013 год. [ на стр. 252-256 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Моделирование информационных процессов систем управления большими данными для решения задач кибербезопасности
- Методика моделирования процесса обнаружения воздушных объектов наземной обзорной радиолокационной станцией в условиях воздействия активных шумовых помех
- Программный комплекс планирования производства на малом предприятии
- Программа идентификации условий теплообмена для изделий плоской формы
- Программный комплекс обнаружения аномалий формы рельсовых путей
Назад, к списку статей



 , закрепленный в центре шара. Тогда ориентация шара задается матрицей перехода
, закрепленный в центре шара. Тогда ориентация шара задается матрицей перехода 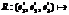 (e1, e2, e3), а точка контакта координатами (x, y)Î
(e1, e2, e3), а точка контакта координатами (x, y)Î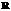 2 в базисе (e1, e2).
2 в базисе (e1, e2).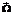 =(W1, W2, W3)Î
=(W1, W2, W3)Î . Задачу о переориентации можно сформулировать как следующую задачу оптимального управления:
. Задачу о переориентации можно сформулировать как следующую задачу оптимального управления: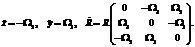
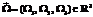 ,
,
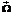 вращается равномерно вокруг неподвижного горизонтального вектора
вращается равномерно вокруг неподвижного горизонтального вектора 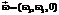 и поворот вокруг вертикальной оси на угол b является симметрией задачи:
и поворот вокруг вертикальной оси на угол b является симметрией задачи: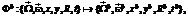


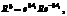
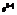 – матрица поворота вокруг оси e3 на угол b. Это позволяет повернуть систему так, чтобы вектор
– матрица поворота вокруг оси e3 на угол b. Это позволяет повернуть систему так, чтобы вектор 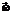 принял вид
принял вид 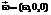 . Тогда уравнения экстремальных траекторий примут наиболее простой вид:
. Тогда уравнения экстремальных траекторий примут наиболее простой вид: (1)
(1)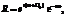 (2)
(2)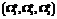 =(W1(0), W2(0), W3(0))=
=(W1(0), W2(0), W3(0))= ;
;  и
и 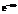 – повороты вокруг векторов
– повороты вокруг векторов 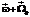 и
и 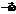 соответственно [10].
соответственно [10].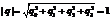 . Напомним, что каждому вращению трехмерного пространства можно поставить в соответствие пару кватернионов
. Напомним, что каждому вращению трехмерного пространства можно поставить в соответствие пару кватернионов 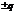 по следующему правилу: если R – вращение трехмерного пространства вокруг единичного вектора
по следующему правилу: если R – вращение трехмерного пространства вокруг единичного вектора  на угол q, то
на угол q, то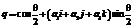 .
. (3)
(3) , где
, где 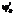 определяется из соотношений
определяется из соотношений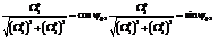
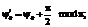
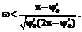 (4)
(4)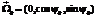 . Подставим выражения для компонент векторов
. Подставим выражения для компонент векторов
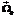 и времени T в (3) и сделаем следующую замену переменных с учетом (4):
и времени T в (3) и сделаем следующую замену переменных с учетом (4):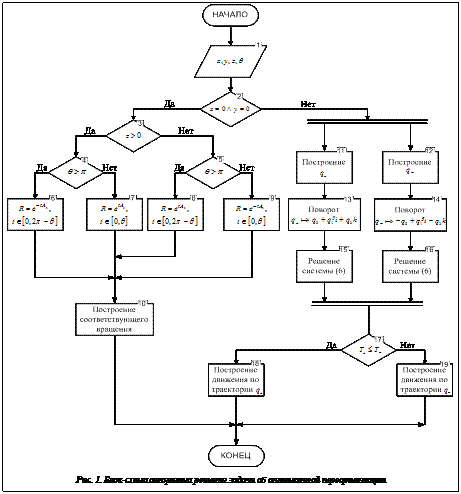
 (5)
(5)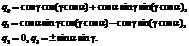 (6)
(6)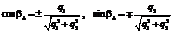 .
.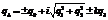 .
.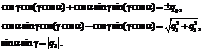
 . Из двух полученных траекторий оптимальной будет та, у которой меньше значение времени T (блок 17). После того как параметры кратчайшей траектории найдены, она может быть построена с помощью формул (1) и (2).
. Из двух полученных траекторий оптимальной будет та, у которой меньше значение времени T (блок 17). После того как параметры кратчайшей траектории найдены, она может быть построена с помощью формул (1) и (2).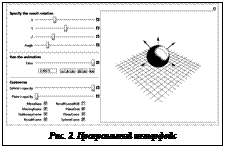 им, что в данной статье явно построен алгоритм решения задачи о переориентации сферы и описана программа, решающая эту задачу. Настоящий алгоритм в дальнейшем можно использовать для перевода шара из произвольного начального состояния в произвольное конечное. Для этого сначала нужно перекатить шар в выбранную точку по прямой без прокручивания и проскальзывания, а затем применить алгоритм, построенный в данной статье.
им, что в данной статье явно построен алгоритм решения задачи о переориентации сферы и описана программа, решающая эту задачу. Настоящий алгоритм в дальнейшем можно использовать для перевода шара из произвольного начального состояния в произвольное конечное. Для этого сначала нужно перекатить шар в выбранную точку по прямой без прокручивания и проскальзывания, а затем применить алгоритм, построенный в данной статье.