Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Эффективный алгоритм размещения деталей произвольной формы на листовом материале
Аннотация:
Abstract:
| Автор: Яремко М.О. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 18937 |
Версия для печати Выпуск в формате PDF (2.31Мб) |
Рассматривается алгоритм раскроя листового материала для фигур произвольной формы, основанный на понятии NFP-полигона и минимизации целевой функции выбора позиции на NFP. Преимуществами рассматриваемого алгоритма является высокая скорость работы, сравнимая со скоростью работы алгоритмов прямоугольной укладки, и эффективность, значительно выигрывающая у алгоритмов, основанных на аппроксимации прямоугольными областями. Кроме этого, отличительными особенностями рассматриваемого алгоритма являются возможности учета отверстий внутри фигуры и раскрой на листах произвольной геометрической формы. Задача размещения деталей произвольной формы на листовом материале состоит в нахождении позиции на листе для каждой из размещаемых фигур таким образом, что фигуры не пересекаются и длинна прямоугольной области, покрывающей множество фигур для каждого листа, является минимальной. Данная задача является NP-сложной даже для случая использования прямоугольных деталей и прямоугольных листов, добавление же условий на произвольную форму фигур и листов еще больше повышает временную сложность (см.: А.Ф. Валеева. Конструктивная эвристика для задачи прямоугольной упаковки. // Вестн. Башк. ун-та. 2006. № 3). В основе механизма решения предложенной задачи лежит механизм построения NFP-многоугольника для двух геометрических областей (см.: Cunninghame-Green, R. Geometry, Shoemaking and the milk tray problem // New Scientist, (1989) 12th August, № 1677). Для двух многоугольников (AB) и любой точки r на плоскости NFP-многоугольником назовем путь, который проделывает точка r при движении многоугольника B (орбитального полигона) относительно A (стационарного полигона), таким образом, чтобы многоугольники A и B касались друг друга, но не пересекались (см. рис.).
1. Основываясь на понятии NFP-полигона, построить контур, находясь на котором размещаемый объект не будет выходить за пределы листа. 2. Выбрать оптимальную позицию на NFP, минимизируя целевую функцию, и разместить объект. 3. Используя булевы операции над полигонами, вычесть из контура листа объект, размещенный на втором шаге. 4. Повторить данную последовательность для всех фигур. Рассмотрим подробнее каждый из перечисленных шагов. Наиболее быстрый алгоритм построения NFP-полигона был оптимизирован для учета отверстий внутри фигур (см.: Burke E.K. Complete and robust no-fit polygon generation for the irregular stock cutting problem // European Journal of Operational Research. 2006. № 179). После построения NFP необходимо найти оптимальную позицию на данном многоугольнике. Предлагается использовать функцию оценки, основанную на минимизации площади выпуклого покрытия всех разложенных фигур (см.: Roger B. Grinde, Tom M. Cavalier. A new algorithm for the minimal-area convex enclosure problem. European Journal of Operational research, 84(1995)). Данный подход имеет высокую вероятность достичь локального минимума решения и имеет высокую трудоемкость, поскольку у функции нахождения выпуклого покрытия высокая временная сложность. Для оптимального размещения двух полигонов предлагается найти такую позицию центра масс размещаемого полигона, для которой минимально значение функции Если при построении NFP было получено несколько контуров, то выбирается контур с минимальной площадью; это обусловливает первоочередность размещения фигуры внутри отверстий существующих фигур. На основе описанного алгоритма разработана подсистема для раскроя листового материала, которая может быть интегрирована в любую САПР. Подсистема реализована для исполнения в среде .net. Для эффективной реализации алгоритма вычитания фигуры из контура листа могут быть использованы известные алгоритмы. Важную роль играет начальная последовательность фигур. Ее оптимизация ведется на основе следующих шагов: - отсортировать фигуры в порядке убывания площадей; - все фигуры, построенные с использованием аппроксимации, заменить фигурами с аппроксимацией меньшим шагом; - все фигуры с небольшой площадью заменить их прямоугольным покрытием; - при расчете оптимального угла поворота использовать алгоритм бинарного поиска из диапазона 0..360. Основываясь на данных ассоциации ESICUP (http://paginas.fe.up.pt/~esicup/), была проведена оценка эффективности предложенного алгоритма. Приведенный алгоритм значительно выигрывает по качеству раскладки у алгоритмов, основанных на аппроксимации прямоугольными областями. Результаты исследования используются в продуктах одного из признанных лидеров систем автоматизации производства для воздухопроводов – компании East Coast (www.eccadcam.com). |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=362 |
Версия для печати Выпуск в формате PDF (2.31Мб) |
| Статья опубликована в выпуске журнала № 3 за 2007 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Электронный глоссарий
- Использование графических постпроцессоров VVG и LEONARDO в вычислительной гидродинамике
- Унифицированный информационный интерфейс и его реализация в комплексной САПР
- Психосемантический подход к оценкам сложности автоматизированных информационных систем
- Нейроподобная сеть для решения задачи оптимизации антенной решетки
Назад, к списку статей



 Процедура размещения фигуры на листовом материале в общем виде может быть сведена к следующей последовательности шагов.
Процедура размещения фигуры на листовом материале в общем виде может быть сведена к следующей последовательности шагов.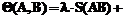
 , где
, где 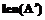 – длина прямоугольника, покрывающего размещаемую фигуру;
– длина прямоугольника, покрывающего размещаемую фигуру; 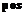 – позиция многоугольника на листе;
– позиция многоугольника на листе; 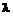 – весовой коэффициент. На практике коэффициент l=0,7 показал наилучшие результаты.
– весовой коэффициент. На практике коэффициент l=0,7 показал наилучшие результаты.