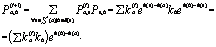Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Верификация мультиагентных систем с помощью цепей маркова: оценка вероятности нахождения агентами оптимального решения
Аннотация:Предлагаются общее описание алгоритма работы определенного семейства мультиагентных систем и некоторые следующие из этого описания оценки свойств систем. В последнее время мультиагентный подход к построению сложных вычислительных систем обретает все большую популярность. Однако связанная с ним теория все еще недостаточно развита. Остаются неясными или недостаточно обоснованными вопросы о том, какого вида системы лучше применять в тех или иных случаях и в чем их преимущество перед другими методами. Отчасти это связано с тем, что в разных областях исследования под мультиагентной системой могут подразумеваться разные понятия. В данной работе выделяется и формализуется отдельное семейство мультиагентных систем, для полученной формализации проводится аналогия с марковскими цепями. Далее с помощью известных свойств марковских цепей исследуются свойства выделенного семейства систем. Для систем, построенных с помощью функции особого вида, доказывается, что вероятность нахождения агентами того или иного допустимого решения тем больше, чем больше значение функции полезности для этого решения.
Abstract:The paper presents general description of meta-algorithm, used by some class of multiagent systems. Nowadays multiagent approach for complex systems building gains more and more popularity. But the theory, connected with it, still remains not developed enough. It’s still unclear or not well-founded, which kind of systems should be used in particular cases, and what advantages these systems have. Partly it’s because multiagent systems may have different meanings in different research areas. In this work one particular class of multiagent systems is considered. Formalization of this class is connected with Markov chains, so we can estimate some properties of these systems using that mathematical instrument. Then, for systems built with some functions, statement is proved that probability of finding allowable solution by agent is higher when fitness function meaning for this solution is higher.
| Авторы: Зайцев И.Д. (zaycev.ivan@gmail.com) - Институт систем информатики им. А.П. Ершова СО РАН (аспирант ), Новосибирск, Россия | |
| Ключевые слова: цепи маркова, случайные процессы, генетические алгоритмы, методы монте-карло, мультиагентные системы |
|
| Keywords: Markov chains, stochastic processes, genetic algorithm, Monte Carlo methods, multi-agent systems |
|
| Количество просмотров: 10414 |
Версия для печати Выпуск в формате PDF (7.95Мб) Скачать обложку в формате PDF (1.45Мб) |
В последние десятилетия мультиагентные системы (МАС) завоевывают все большую популярность. Высокопроизводительные вычислительные системы строятся изначально как распределенные системы с множеством потоков управления и распределенными данными. Даже в пользовательском аппаратном обеспечении используются многоядерные и векторные процессоры. Все это де- лает востребованной концепцию МАС, в рамках которой вычислительная система представляется как набор принимающих решения и обменивающихся информацией агентов, в достаточной мере не зависящих друг от друга. Однако необходимо отметить, что теория МАС недостаточно проработана. Отчасти это объясняется тем, что понятие МАС довольно размыто, поскольку в разных областях исследования и применения под ним понимаются довольно разные вещи. Все это усложняет не только поиск и определение свойств, верификацию МАС в общем случае, но и саму формализацию понятий агента, системы, программы и т.п. Закономерными в данном случае являются предварительное выделение некоторого семейства МАС, устроенных схожим образом, обоснование их значимости, формализация и исследование их свойств с помощью уже существующего математического аппарата с возможной корректировкой этого аппарата с учетом специфики задачи. Например, в рамках работы [1] было выделено семейство МАС, использующих парадигмы логического программирования, и предположено, что процесс обмена информацией между объектами подвержен случайным задержкам с заданным распределением вероятности. В данном случае представляют интерес МАС, используемые в имитационном моделировании в области экономики, общественных наук и биологии. В предлагаемой работе выделено такое семейство МАС, показано, что в него входят также МАС, используемые при решении оптимизационных задач, в частности, реализующие эволюционные алгоритмы. Семейство синхронных стохастических мультиагентных моделей В различных МАС требования к тому, что считать интеллектуальным агентом, существенно разнятся. Агент может иметь сложное внутреннее устройство, обладать довольно развитым искусственным интеллектом, а также действовать реактивно по фиксированному простому алгоритму. Как правило, количество используемых агентов обратно пропорционально сложности их внутренней организации. В крайних случаях имеются следующие типы систем. МАС, состоящая из 2-3 высокоинтеллектуальных агентов (включающих в себя, как правило, другие системы искусственного интеллекта, например экспертные), со сложным, продуманным протоколом для общения, установления слаженности действий. МАС, состоящая из большого числа (до нескольких тысяч или даже десятков тысяч) простых агентов, взаимодействующих главным образом со средой, а не друг с другом, с простым, но не строго детерминированным поведением. Такие системы, как известно, способны демонстрировать роевой интеллект (swarm intelligence), приспосабливаться к меняющимся условиям, находить ниши с оптимальным значением тех или иных показателей. На этом, в частности, основываются методы муравьиной колонии, роя частиц, другие эвристические методы [2, 3]. В экономике и общественных науках создать продуманную и сложную модель действующего субъекта (то есть построить высокоинтеллектуального агента) подчас бывает довольно сложно, поскольку это требует наличия высокоразвитой теории психологии субъектов, четкого знания алгоритмов, используемых ими для принятия тех или иных решений. Эффективнее принять простую схему действий агента, а отклонения от нее считать случайной величиной с заданным распределением. Таким образом, получаются модели, более близкие ко второму крайнему случаю. При этом полезно рассматривать агентное моделирование вместе с другими методами имитационного моделирования [4]. Конечная цель агента в таких системах (и направленная к ее достижению деятельность) определяется поиском более или менее удачного приближения к наилучшему решению какой-то определенной задачи. Например, поиск глобального максимума некоторой функции max(f) с помощью приближенных методов или эвристик, харак- терных для задач искусственного интеллекта. Решение задачи производится поэтапно. Сначала агенты ищут это приближение (каждый по собственному представлению о функции и своему алгоритму с использованием доступных сведений из среды). Затем устанавливают некоторые значения среды согласно найденному решению. После этого снова ищут приближение, исходя из уже изменившихся значений переменных среды. В последовательном повторении этих двух этапов и заключается имитационное моделирование. Для введения математического описания этого процесса конкретизируем рассматриваемое семейство МАС и используемые понятия так, чтобы не потерялась их ценность. Для этого рассмотрим МАС сходного с описанным устройства, применяемые в задачах оптимизации (а также методы оптимизации, реализовать которые можно с помощью таких МАС). Пошаговый случайный поиск Вероятностные методы решения задач (методы Монте-Карло) занимают особое место среди методов поиска решений. С одной стороны, их использование, как правило, оказывается оправданным в том случае, если свойства искомого решения и его место среди допустимых решений (например, максимизируемой функции в случае задачи поиска максимума) недостаточно изучены или вообще трудно поддаются установлению, например, в численном интегрировании сложных функций в пространствах большой размерности. С другой стороны, многие случайные вычисления могут быть осуществлены независимо друг от друга, что делает довольно удобным процесс их распараллеливания и обеспечивает рост скорости вычислений с увеличением числа независимых вычислителей. Например, метод иглы Бюффона для определения значения числа Пи при последовательной генерации случайных чисел существенно проигрывает по времени другим численным методам. Однако, поскольку генерация нескольких случайных чисел может быть проведена независимо, то, располагая произвольно большим количеством вычислителей, можно произвести генерацию сколь угодно большого набора случайных чисел за время, ограниченное константой. В реальности же вычислительные системы имеют ограниченное количество вычислителей. В связи с этим может быть случайно сгенерировано лишь определенное число решений. Однако зачастую обмен информацией о полученных решениях помогает сузить область поиска или задать направления для дальнейшего поиска, в общем, сохраняя вероятностный характер найденного решения, увеличить вероятность нахождения оптимума. На этом принципе построены многие эвристические методы поиска оптимального решения [5]. Итак, представляется интересной следующая математическая модель работы МАС. Пусть даны n агентов (A1, …, An). Целью каждого агента является нахождение максимума заданной функции f(x) (назовем ее целевой) на заданной области D. Действия агентов определяются следующим алгоритмом. Изначально каждый агент получает начальное решение x0,j (j=1, …, n). Для краткости обозначим совокупность значений переменной x у всего набора агентов как X=. Таким образом, агенты получают (или находят случайным образом) начальный набор X0 и начинают пошагово искать максимум целевой функции. Опишем алгоритм их действий (в общем виде) на i-м шаге. У каждого агента имеется значение xi,j (то есть задан набор Xi). Сначала каждый агент вычисляет значение целевой функции на данном ему значении x (f(xi,j) обозначим для краткости fi,j, а набор значений f у всех агентов – Fi). Затем агенты обмениваются информацией о найденных решениях (каждый агент сообщает каждому или передает в общую память значения xi,j, fi,j). Исходя из полученных решений, каждый агент определяет следующее значение xi+1,j=gi,j(Xi, Fi). Обозначим его кратко как Xi+1=Gi(Xi, Fi), где функция Gi(Xi, Fi) определяет набор . Функции gi,j(Xi, Fi) в общем случае могут не быть строго детерминированы, и для многих мультиагентных моделей это действительно так. Поскольку вычисление значений функций f и g осуществляется агентами независимо, можно ожидать пропорционального количеству агентов прироста производительности работы системы в случае, если деятельность каждого агента реализуется отдельным вычислителем (например, процессором или одним ядром многоядерного процессора), а обращение вычислителей к общей памяти происходит за пренебрежимо малое время (в сравнении со временем, необходимым на вычисление значений функций f и g). Представление генетических алгоритмов в рамках полученной модели. Деятельность довольно большого круга МАС можно представить в предложенном общем виде. Интересным примером является мультиагентная реализация генетического алгоритма (ГА). Возьмем за основу описание ГА, данное в [6]. Предположим, что агенты – это селекционеры, выращивающие, отбирающие и скрещивающие лучших особей. Количество селекционеров равно количеству особей в одной популяции. Сначала селекционеры получают начальную популяцию X0. Затем каждый для своей особи вычисляет значение функции полезности (F(X0)=). Потом каждый агент-селекционер выбирает сообразно значениям функции полезности случайным образом две особи-решения и скрещивает их (алгоритм выбора и алгоритм скрещивания могут быть разными в разных реализациях ГА). Таким образом определяется значение функции gi,j(Xi,Fi). Формально функцию g можно определить через умножение случайным образом составленных матриц на векторы, что, например, проделано в [7]. ГА применяются в основном для задач, в которых функция полезности имеет достаточно сложный вид, что препятствует решению ее точными методами. Это означает, что зачастую вычисление функции полезности представляет собой весьма трудную задачу и основное время в реализации ГА занимает вычисление функции полезности для одной особи. Представление ГА в виде МАС, где каждому агенту соответствует особь в популяции, позволяет существенно сократить время работы ГА. Кроме того, подобное представление дает возможность применить математические методы для оценки свойств описываемой им МАС. Исследование свойств полученной модели МАС с помощью цепей Маркова Формализуем и сузим полученное представление МАС. Предположим, что область D является конечным множеством (что верно для многих систем), а функция g и начальные значения X0 – это случайные величины с заданным распределением. В начальный момент времени имеется набор X0. На каждом следующем шаге получаем новый набор Xi+1=Gi(Xi,Fi). Поскольку Fi=F(Xi), а функция F задана изначально, то получается, что Gi зависит только от Xi. Выразим это кратко: Xi+1=Gi(Xi). Нетрудно заметить, что это описание марковского процесса с дискретным временем и пространством – последовательность случайных чисел Xi, где i обозначает момент времени и каждое следующее значение зависит только от настоящего. Для многих МАС (в частности, представляющих ГА) Gi(Xi) не зависит от i. В таком случае полученная марковская цепь (МЦ) является также однородной. Множеством состояний S будет множество наборов X= | xjÎD. Обозначим m=|S|= |D|n, S={s1, …, sm}. Допустим, что a, b, c – произвольные элементы множества S. Начальным распределением будет вектор p=(p1, …, pm)T. Для удобства в качестве индексов используем элементы множества S. Тогда получим, что вектор p состоит из элементов pa=p(X0=a). Матрица переходных вероятностей на i-м шаге P(i) в таком случае состоит из элементов Pab(i)= =p(Gi(a)=b). В дальнейшем будем рассматривать однородные МЦ, иными словами, Pab(i)=Pab и не зависит от i. Элемент P(i)ab будет обозначать вероятность попадания цепи из состояния a в состояния b по прошествии i шагов. Такое описание позволит воспользоваться изученными свойствами МЦ для оценки эффективности и определения свойств МАС, подпадающих под описанную модель. В частности, в работах [1, 8] проводится оценка сложности верификации МАС (хотя и другого вида), представленных в виде МЦ. Небезынтересным также является поведение систем после довольно значительного числа шагов. Как известно, для особого семейства МЦ, называемых эргодичными, по прошествии длительного периода времени вероятность попадания случайной величины в то или иное состояние перестает зависеть от начального состояния цепи. Иными словами, при i→∞ P(i)ab=P(i)b. Условия эргодичности и ее математическое определение даны, например, в [9]. Для данного случая это условие можно выразить так: возведенная в некоторую степень матрица перехода не содержит нулевых элементов. Иными словами, у МЦ есть вероятность через определенное число шагов перейти из любого состояния в какое-либо другое. Полезно было бы оценить вероятность получения того или иного состояния в зависимости от значения максимизируемой функции f в нем. Высокое значение вероятности для состояний с более высоким значением функций в данном случае гарантировало бы большую вероятность нахождения максимума (вне зависимости от начального решения). Введем для оценки полезности состояния МЦ функцию h(Xi)=max(f(xi,1), …, f(xi,n)), где Xi=. Проведем сначала грубую и простую оценку вероятности, взяв довольно сильное условие. Предположим, что h(b)≥h(c)ÞPab≥Pac "aÎS. Докажем, что также P(i)ab≥P(i)ac для любого i. Имеем Из теоремы эргодичности [9] получаем, что при количестве пройденных шагов, стремящемся к бесконечности, вероятность попадания в то или иное состояние не зависит от начального набора X0. А из принятого здесь условия получаем, что вероятность попадания в то или иное состояние тем выше, чем выше соответствующее ему значение функции полезности h(X). Однако полученной оценкой сложно воспользоваться, поскольку трудно построить такую функцию G, которая удовлетворяла бы поставленным условиям. В связи с этим может быть предложено более мягкое начальное условие, которое не ослабляет следствие. Предположим, что изначально разрешены переходы не из каждого в каждое состояние, а только в некоторые из них и лишь для них выполняется сформулированное выше условие. Иными словами, h(b)≥h(c); Pab, Pac≠0ÞPab≥Pac "aÎS. К сожалению, для такого общего случая следствие может и не выполняться. Для выполнения следствия необходимо поставить вероятность перехода в определенное соответствие со значением функции полезности в искомом состоянии. Пусть для каждого состояния a определено множество соседних состояний S(a)={b | Pab≠0}. Определим
Выделенная в скобках сумма представляет собой нормировочную константу. Таким образом, для матрицы перехода после i шагов верно то же представление элементов, что и для начальной матрицы перехода. Из условий эргодичности получаем, что в возведенной в некоторую степень матрицы перехода все элементы будут ненулевыми. Но из формулы для элементов матрицы перехода, возведенной в произвольную степень, получаем искомое условие h(b)≥h(c)ÞPab≥Pac "aÎS. Таким образом, для заданной функции g получаем верность того следствия, что вероятность нахождения решения тем больше, чем больше значение целевой функции. Литература 1. Валиев М.К., Дехтярь М.И. Вероятностные мультиагентные системы: семантика и верификация // Вестн. ТГУ: сер. Прикладная математика. 2008. № 35 (95). С. 9–22. 2. Pham D.T., Ghanbarzadeh A., Koç E., Otri S., Rahim S., and Zaidi M. The Bees Algorithm – Novel Tool for Complex Optimisation Problems. Proc. of IPROMS 2006 Conf., 2006, pp. 454–461. 3. Raudenska L. Swarm-based optimization. Kvalita Inovacia Prosperita. Quality Innovation Prosperity XIII/1 – 2009, no. 1, pp. 45–51. 4. Замятина Е.Б. Современные теории имитационного моделирования: спец. курс. Пермь: ПГУ, 2007. 119 с. 5. Кочетов Ю.А. Вероятностные методы локального поиска для задач дискретной оптимизации // Дискретная математика и ее приложения: сб. лекций молодеж. и науч. школ по дискрет. матем. и ее приложениям. М.: МГУ, 2001. С. 87–117. 6. Богатырев М.Ю. Инварианты и симметрии в генетических алгоритмах // Искусственный интеллект: тр. XI национальн. конф. по искусствен. интеллекту с междунар. участием «КИИ-2008». М.: Ленанд, 2008. Т. 1. Сек. 3. 7. Курейчик В.М., Лебедев Б.К. Определения и основные понятия генетических алгоритмов // III Всерос. межвуз. конф. молодых ученых СПбГУ ИТМО. URL: http://faculty.ifmo.ru/ csd/files/kureichik_v_m_lebedev_b_k_internet_lecture.pdf (дата обращения: 13.12.2012). 8. Бурмистров М.Ю., Валиев М.К., Дехтярь М.И., Диковский А.Я. О верификации динамических свойств систем взаимодействующих агентов: тр. X национальн. конф. по искусствен. интеллекту с междунар. участием. М.: Физматлит, 2006. 9. Булинский А.В., Ширяев А.Н. Теория случайных процессов. М.: Физматлит, 2005. 408 с. References 1. Valiyev M.K., Dekhtyar M.I. Vestnik Tver State Univ. Seriya “Prikladnaya matematika” [The bulletin of TvSU. “Applied Mathematics” Series]. 2008, no. 35 (95), pp. 9–22. 2. Pham D.T., Ghanbarzadeh A., Koç E., Otri S., Rahim S., Zaidi M. Proc. of IPROMS 2006 Conf. 2006, pp. 454–461. 3. Raudenska L. Quality Innovation Prosperity XIII/1 – 2009, pp. 45–51. 4. Zamyatina E.B. Sovremennyye teorii imitatsionnogo modelirovaniya: spetsialny kurs [Modern theories of imitation modeling: special course]. Perm, Perm State Univ. Publ., 2007 (in Russ.). 5. Kochetov Yu.A. Diskretnaya matematika i eyo prilozheniya. Sbornik lektsiy molodyozhnykh i nauchnykh shkol po diskretnoy matematike i eyo prilozheniyam [Discrete math and its appli- cations. Lectures of youth and scientific schools on discrete math and its applications]. Moscow, MSU Publ., 2001, pp. 87–117 (in Russ.). 6. Bogatyrev M.Yu. Trudy 11 nats. konf. po iskusstvennomu intellektu s mezhdunar. uchastiem (KII-2008) [Proc. of 11th national conf. on artificial intelligence with int. participation (CAI-2008)]. 2008, Dubna, vol. 1, section 3. 7. Kureychik V.M., Lebedev B.K. 3 Vseross. mezhvuz. konf. molodykh uchyonyh SPbGU ITMO [3rd all-Russian conf. of young scientists SPbSu IFMO]. Available at: http://faculty.ifmo.ru/csd/files/kureichik_v_m_lebedev_b_k_internet_lecture.pdf (accessed 13 December 2012). 8. Burmistrov M.Yu., Valiev M.K., Dekhtyar M.I., Dikovskiy A.Ya. Trudy 10 nats. konf. po iskusstvennomu intellektu s mezhdunar. uchastiem [Proc. of 10th national conf. on artificial intelligence with int. participation]. Moscow, Fizmatlit Publ., 2006. 9. Bulinskiy A.V., Shiryaev A.N. Teoriya sluchaynykh protsessov [The stochastic processes theory]. Moscow, Fizmatlit Publ., 2005 (in Russ.). |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=3664 |
Версия для печати Выпуск в формате PDF (7.95Мб) Скачать обложку в формате PDF (1.45Мб) |
| Статья опубликована в выпуске журнала № 4 за 2013 год. [ на стр. 96-100 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Моделирование социальных процессов и мультиагентный подход
- Метод автоматизации проектирования распределенной реляционной базы данных
- Алгоритм и программная реализация синтеза модели объекта испытаний на основе решения уравнения непараметрической идентификации
- Решение задачи структурного построения программного обеспечения интеллектуального датчика влажности
- Архитектура системы распределенного вывода на основе прецедентов для интеллектуальных систем
Назад, к списку статей



 (поскольку Ps,b≥Ps,c "sÎS).
(поскольку Ps,b≥Ps,c "sÎS).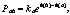 "bÎS(a). Коэффициент ka подбирается специально таким образом, чтобы сумма вероятностей перехода из состояния a в другие состояния равнялась 1. Для остальных состояний вероятность перехода из состояния a будет нулевой. Докажем, что для такой матрицы перехода конечное условие будет выполняться. Действительно,
"bÎS(a). Коэффициент ka подбирается специально таким образом, чтобы сумма вероятностей перехода из состояния a в другие состояния равнялась 1. Для остальных состояний вероятность перехода из состояния a будет нулевой. Докажем, что для такой матрицы перехода конечное условие будет выполняться. Действительно,