Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Ontologies in the “Binary Model of Knowledge”
Abstract:Онтология представляет в формальном виде общее знание о предметной области для данного приложения. Конкретное знание для приложения выражается с помощью фактов, структурированных в соответствии с онтологией. База фактов представляет текущее состояние приложения. В настоящее время известно много формализмов для спецификации онтологий. Наиболее разработанными и исследованными являются языки дескриптивных логик. На основе этих логик были разработаны языки семейства OWL, которые признаны стандартными комитетом W3C. Однако эти языки не являются типизированными и поэтому лишены тех преимуществ, которыми обладают типизированные языки. В настоящей работе дается краткое описание типизированных концептуальных языков для разрабатываемой системы «Бинарная Модель Знаний» (БМЗ), предназначенной для построения и анализа онтологий и баз фактов. В частности, описаны язык структурной спецификации (для определения структуры индивидных объектов и фактов), язык запросов к базам фактов, язык логической спецификации (для спецификации экстенсионалов понятий), язык продукций (для состоятельного преобразования баз фактов). В работе также показана возможность применения системы БМЗ к задаче прогнозирования автодорожных пробок.
Аннотация:Ontology represents some general knowledge about a given problem domain. A concrete knowledge is ex-pressed by facts which are structured according to the ontology. The set of these facts, the so -called fact base, can be consid-ered as a state or an instance of the ontology. Nowadays there are a lot of formal description to specify ontologies. The mos t elaborated and researched are description logics languages. Based on these logics, OWL (Web Ontology Languages) has been developed. OWL is recognized by W3C. But OWL is not typed language. That is why it does not have a number of ad-vantages that typed languages have. The article describes briefly typed conceptual languages for the developed system “Bin a-ry Model of Knowledge” (BMK). The system is intended for specifying and interpreting ontologies and their fact bases. In particular, there are descriptions of: (1) language LSS for structural specification (to define concepts universes); (2) language LDT for definition of data types язык; (3) language LLS for logical specification (to define concept extensions); (4) language LP of productions (for fact bases transformations). The possibility to apply BMK to the problem of forecasting road traffic jams is shown
| Авторы: Plesniewicz G.S. (salve777@mail.ru) - Национальный исследовательский университет (профессор ), Москва, Россия, Ph.D, Karabekov B.S. (salve777@mail.ru) - Казахский институт путей сообщения, Алматы, Казахстан, Ph.D | |
| Keywords: интеллектуальные транспортные системы, продукционный вывод, конъюнктивные запросы, базы фактов, спецификация онтологий, онтологии |
|
| Ключевые слова: intelligent trans-portation systems, productional inference, conjunctive queries, fact bases, ontology specification, ontologies |
|
| Количество просмотров: 4938 |
Версия для печати Выпуск в формате PDF (7.83Мб) Скачать обложку в формате PDF (1.01Мб) |
Informally, ontology is a specification of conceptualization. It represents some general knowledge about a given problem domain. A concrete knowledge is expressed by facts which are structured according to the ontology. The set of these facts, the so-called fact base, can be considered as a state or an instance of the ontology. The ontology taken together with the fact base forms the knowledge base. A standard language for specifying ontologies is OWL [1]. It is the language with formally defined semantics based on description logics [2]. So OWL provides the representation of classes, properties (roles, attributes), individual objects and values. It is not typed language. But it is known that typed languages have a number of advantages [3]. We are developing the system of conceptual languages called “Binary Model of Knowledge” (BMK) and the means for their interpretation. This system is intended to specify ontologies and fact bases. Besides, the languages of BKM are typed. In this paper we give a brief description of BMK and show the possibility to apply BMK to the problems of designing intelligent transportation systems. Brief description of the “Binary Model of Knowledge” Ontologies in BMK are formed from concepts of two kinds – classes and (generic) binary links. A concept C has the extension EC (i.e. the set of all names which denote the instances of the concept C) and the universe UC (i.e. the set of all names which can denote the instances). So ECÍUC, and the names from EC denote individual objects of problem domain if C is a class, and denote binary links (binary relations) between individual objects if C is a binary link between individual objects. The function “name→object” is called reference and is denoted by ref. Two names e and e’ are called coreferential if ref(e)=ref(e’). In this case we write e~e’. In general, EC contains different coreferential names. In the BMK languages, simple and composite names are used. Composite names are defined by some constructs. The following notation is used the constructs: · –C (or –L) denotes the class (binary link) whose instances are not instances of the class C (binary link) i.e. U–C=UC, E–C=UC\E (U–L=UL, E–L=U\EL); · C(*) denotes the class whose instances are all finite sets of instances of C i.e. UC(*)={{e1, e2, …, en}}|eiÎUC, 1≤i≤n, n=0, 1, …}, EC(*)={{e1, e2, …, en}}|eiÎEC, 1≤i≤n, n=0, 1, …}; · C(p, q) (p and q are nonnegative numbers or q is the symbol *, and p≤q) denotes the subclass of C(*) defined by the condition p≤n≤q i.e. UC(p,q)={xÎUC|p≤|x|≤q}, EC(p,q)={xÎEC|p≤|x|≤q}. (If q is the asterisk then p≤|x|≤q should be replaced with p≤|x|.) · L((p, q)(r, s)) (p≤q, r≤s or q is the asterisk, and s is the asterisk) denotes the binary link whose instances are finite sets of instances of the binary link L. Here if an instance of L((p, q)(r, s)) is considered as a bipartite graph then the degree of any left (right) node is concluded between the numbers p and q (r and s). · C1|C2|…|Cn denotes the concept such that x is its instance if and only if x is an instance of exactly one of the concept Ci. The system BMK includes the following languages: − language LSS for structural specification. Statements of LSS define concepts universes; − language LDT for definition of data types. Statements of LDT define abstract data types which are used as domains of attributes; − language LLS for logical specification. Statements of LLS define concept extensions; − language LF of facts. Statements of LF define facts; − language LQ of queries. Statements of LQ are queries to fact bases; − language LP of productions. Statements of LP are rules for fact bases transformations. An ontology in BKM is a finite set O of statements from LSS U LDT U LLS. Languages LSS and LDT. Statements of LSS are composed from elementary statements of the forms: C, C[E], C[A:E], C[A:T], (C L D), (C L D)[E], (C L D)[A:E], (C L D)[A:T], (1) where C, D, E are names of classes, L is a name of a binary link, A is an attribute, and T is a type specification written in LDT. Here C, D and L are simple names, but E can be a composite name. The name C and the expression (C L D) are heads in these elementary statements. Elementary statements with identical heads can be merged into one LSS statement. For example, C[E], C[A: D(*)], C[B: (Integer,Integer)] are merged into one statement C[E, A: D(*), B: (Integer,Integer)]. (2) The statements (1) define (correspondingly) the following universes: UC=SurrUIname, UC=SurrUInameU{[E : x] | x UC=SurrUInameU{[A : x] | x UC=SurrUInameU{[A : x] | x UL=SurrUInameU{[C: x, D: y]|x, yÎSurr}, UL=SurrUInameU{[C: x, D: y, E: z]|x, y, zÎSurr}, UL=SurrUInameU{[C: x, D: y, A: z]|x, y, zÎSurr}, UL=SurrUInameU{[C: x, D: y, A: z]|x, y, zΓT”}. Here Surr denotes the set (primitive data type) {#1, #2, #3, …} of so-called surrogates which are used as identifiers of individual objects; Iname denotes the set of all character strings which are used as individual objects names; “T” denotes the set of all elements of the data type defined by the specification T. The statements (1) are also constrain the extensions of C and L. For example, the statement C[A:E] limits tuples [A: x] from EC to the condition xÎEE. The universe of the class C defined by (2) is consisted of elements of SurrUIname and all tuples [E: x, A: {x1, x2, …, xn}, B: (y, z)] with x, xjÎSurr, n=0, 1, 2, … and y, zÎInteger. In EC only those tuples enter that satisfy the conditions x Let us consider examples of specifications. Example 1. The following text in LDT defines the data type of all binary trees with nodes labeled with integers. The data type includes the function (operation) refl giving the specular reflection of binary trees. TYPE BinTree=Integer|(Intrger, BinTree, Integer; FUN refl: BinTree®BinTree refl(X):=X IF X IN Integer; refl((X, Y, Z)):=(refl(Z), Y, refl(X)). FUN sum: BinTree®Integer sum(X):=X IF X IN Integer sum((X, Y, Z)):= sum(X)+Y+sum(Z). END Example 2. The following LSS statements can be considered as a fragment of an ontology designed for representing knowledge about educational process in a university. These formal statements have self-evident informal readings. For example, (4) can be read as “a student passed examination in some subject at some date, received some mark, and some teacher was an examiner”. Student[Full_name: String, Belongs_to: Stud_group, Birth_year: Student]. (3) Stud_group[Title: String, Tutor: Student] (Student Passed_exam Subject)[Date: Date, Mark: {3,4,5}, Examiner : Teacher]. (4) Department[Title: String, Staff: Teacher(*) | Laborant(*)]. Teacher[Full_name : String, Position: {Professor, Assistant}, Work_at: Department]. Subject[Name: String, Is_conducted_by: Teacher]. Language LF. Facts are expressions for the following assertions: e EC, eÏEC, (e, e’)ÎEL, eÏEL, t.AÎEC, t.AÏEL, t.A=v, t.A≠v, (5) where C is a class name, L is a link name, A is an attribute, v is a value (element of data type), e, e’ are names of individual objects, and t is a tuple i.e. expression of the form [A1: e1, A2: e2, …, An: e2]. By t.A we denote the result of application to the tuple t so-called dot operation: if A=Aj then t.A=ej. In language LF, facts (5) are written as +e IN C, –e IN C, +e L e’, – e L e’, +t.A IN C, –t.A IN C, t.A=v, t.A/=C. In BMK fact bases are represented by tables. For example, let us take the binary link Passed_exam from Ex. 1. The structure of this concept is declared by (3). The head of the table corresponding to Passed_exam is as follows:
If (x, y, z, u, v, w, r, s) is a row of the table then: − x is a surrogate that identifies a situation “passed examination”; − yÎ{+, –} and y=+ if the student passed examination, y=– if he did not pass examination; − z is a list of names which are coreferential to x; − u is the full name of a student; − v is a surrogate of a subject in which the student was examined; − w is the date of the examination; − r is the mark which was received by the student if he passed examination, and nil if he did not passed examination; − s is the surrogate for the examiner. Note that the surrogate x and the tuple [Coref: z, Student: u, Subject: v, Date: w, Mark: r, Examiner: s](6) are two coreferential names for the situation with the surrogate x. Also, if t is the tuple (6) and z is the list [e1, e2, …, en] then x~e1~e2~…~en~t. Thus the row (x, y, z, u, v, w, r, s) represents the following facts: +x IN Passed_exam (if y=+), –x IN Passed_exam (if y= –), x.Coref=z, x.Belongs_to=v, x.Birthday=w. In language LF there are operators for inserting and deleting facts: INSERT f and DELETE f where f is a fact. Language LQ. This language includes so-called conjunctive queries. Examples 3. Let O1 be the set of five statements given in Ex. 2. Consider queries to fact bases which are states (instances) of the ontology O1. Query 1. Find all students from the student’s group A13-03 who were born in 1993. ?X.Full_name – X IN Student; X.Belong_to.Title=A13-03; X.Birth_year=1993. Another representation of the query in LQ: ?X.Full_name – X IN Student(Belong_to.Title=A13-03; Birth_year=1993). Query 2. What is the name of the tutor of the student’s group A13-09? ?X.Tutor.Full_name – X IN Stud_group; X.Title=A13-09. Another representation of the query in LQ: ?X.Tutor.Full_name – X IN Student(Title=A13-03). Query 3. What students from the student’s group A13-09 passed examination in graph theory at 10/01/2013 and received the mark 4? ?X.Full_name – (X Passed_exam:Y Z); X.Belongs_to.Title = A13-09; Z.Name = ’graph theory’; Y.Mark = 4; Y.Date = 10/01/2013. Query 4. What students from the group A13-09 didn’t pass examination to Professor Valery B. Tarasov? ?X.Full_name – (X -Passed_exam:Y Z); X.Belongs_to.Title=A13-09; Y.Examiner.Full_name=‘Vadim N. Vagin’ Query 5. Whether the tutor of the group A13-09 passed examination in the theory of graphs? ? – X IN Stud_group; (X.Tutor Passed_Exam Y); X.Title = A13-05; Y.Name=‘graph theory’. In general, a conjunctive query has the form ?γ – δ1; δ2;…; δn, where γ is the head and δ1; δ2; …; δn is the body of the query. The head γ is a term or a sequence of terms: γ=τ or γ=(τ1, τ2, …, τm). Terms are formed from individual variables and variables with selectors by applying operations of abstract data types. Semicolons in the body denote conjunctions. A selector is an expression of the form A1.A2.….An where Ai are attributes. A variable X with a selector S is the expression X.S. (Note, it is possible n=0, and then we have the empty selector □ for which Х.□=Х.) Components δi of the query body have the forms: X.S θ c, X.S1 θ Y.S2, X.S IN C, X.S IN C(α), (X L Y), (X L Y Z), where C and D are classes; L is a binary link; X, Y, Z are variables; c is a constant; S, S1, S2 are selectors; θ is a comparison relation (in particular, θÎ{=, £, ³, <, >}); α is an attribute condition which is an expression of the form λ1; λ2; …; λn where every λi has the form S θ c or S1 θ S2. Since for fact bases in BMK the tabular representation is accepted, it is possible to translate conjunctive queries into SQL. We have developed such translator. For example, the translator transforms the Query 2 into the following SQL query: SELECT DISTINCT __0.Title FROM (SELECT id, Full_name FROM Student) AS __0 CROSS JOIN SELECT id, Tutor FROM Stud_group) AS __1 CROSS JOIN (SELECT id, Team FROM Student). Language LLS. In this language there are several types of logical statements. We consider some of the types. Let C and D be concepts with the same universe: UC=UD=V. Then it is possible to apply to them Boolean operations. The concepts C AND D, C OR D and –C are defined as follows: UC AND D=UC OR D=UC OR D=V, EC AND D=EC∩ED, EC OR D=ECUED. The following logical statements belong to LLS: C ISA D, C(α) ISA D, C ISA D(β), C(α) ISA D(β), C=D, C(α)= =D, C=D(β), C(α)=D(β), C.S ISA D.T, C.S=D.T, where α, β are attribute condition and S, T are selectors. The relation ISA between the concepts C and D means that for any instance x of C there is an instance y of D such that x is coreferential to y. The relation “=” between C and D takes place if C ISA D and D ISA C. The expression C(α) defines the class with UC(α)=UC and EC(α) consists of all xÎUC such that x satisfies the attribute condition α. The language LSS includes the sublanguage LSS-0 which extends the descriptive logic language ALC [2]. At first we consider the example of an ontology written in LSS-0. Example 4. In 1978 year L. Schubert set up the following problem that became well known since, in spite of its apparent simplicity, it turned out (after formalization in clause-based logic) to be too hard for inference by resolution. (A) Wolves, foxes, birds, caterpillars, and snails are animals. (B) There are some of each of them. (C) There are some grains. (D) Grains are plants. (E) Every animal either likes to eat all plants or all animals much smaller than itself that like to eat some plants. (F) Caterpillars are smaller than birds. (G) Snails are smaller than birds. (H) Birds are smaller than foxes. (I) Foxes are smaller than wolves. (J) Wolves do not like to eat foxes or grains. (K) Caterpillars and snails like to eat some plants. (L) There is an animal that likes to eat some plants. The problem consists in the proof that (L) follows from (A), (B), …, (K). The assertions (A), (B), …, (L) are written in LLS-0 as follows. O-st ={Wolf ISA Animal. Fox ISA Animal. Bird ISA Animal. Caterpillar ISA Animal. Snail ISA Ani9mal. EXIST Wolf. EXIST Fox. EXIST Bird. EXIST Caterpillar. EXIST Snail. EXIST Grain. Grain ISA Plant. EACH Animal:Х (Eat SOME Plant OR Eat EACH Animal THAT (Smaller X) AND Ест SOME Растение). EACH Caterpillar Smaller EACH Bird. EACH Snail Smaller EACH Bird. EACH Bird Smaller EACH Fox. EACH Fox Smaller EACH Wolf. EACH Wolf –Ест EACH Fox. EACH Wolf –Ест EACH Grain. EACH Caterpillar Ест SOME Plant. EACH Snail Ест SOME Plant.} The assertion (L) is written as EXIST Animal THAT Eat SOME Animal THAT Eat EACH Grain. (7) LSS-0 statements are formed from terms of three types: C-terms, L-terms, P-terms. C-terms denote classes of individual objects. They are interpreted as subsets of the set Surr of all surrogates. L-terms denote binary links. They are interpreted as subsets of the set (Surr, Surr) of all pairs of surrogates. P-terms denote unary predicates on U. They are interpreted as functions from U to the data type Boolean={true, false}. Here are examples of C-terms, L-terms and P-terms (correspondingly): Animal, –Animal, Wolf AND Fox, Animal THAT Eat EACH Grain; Smaller, Eat, –Eat, Smaller AND -Eat; Smaller wolf2, Smaller X, Smaller EACH Fox, Eat SOME Plant. We use the following variables in the description of syntax and semantics of LSS-0: c for individual constant; C, C1, C2 for names of classes; L, L1, L2 for names of binary links; P, P1, P2 for predicates; S, S1, S2 for LSS-0 statements; for parameters Х, Х1, Х2, ... If exp is any expression then ||exp|| will denote the value of exp under a given interpretation. Syntax of C-terms: С ::= –C | C :V | (C1 AND C2) | (C1 OR D2) | C THAT P | L SOME C | L ONLY C | Cname where Cname is the data type of all names for concept names. Semantics of C-terms: || – C||=Surr \ ||C||, ||C1 AND C2||=||C1|| ∩ ||C2||, ||C1 OR C2||=||C1||È||C2||, ||L SOME C||={xÎSurr | $yÎ||C||.(x,y) Î||L|| }, ||L ONLY C||={xÎSurr | "yÎSurr.(x,y) Î||L||→xÎ||C||}, ||C THAT P|| ={x ||D : V||=||V||. Syntax of L-terms: L ::= – L | L: V | (L1 AND L2) | (L1 OR L2) | INV(L) Semantics of L-terms: || – L|| (Surr, Surr) \ ||C||, ||L: V||=||V||, ||L1 AND L2||=||L1|| ∩||L2||, ||L1 OR L2||=||L1||È||L2||, ||INV(L)||={(y, x) | (x, y)Î||L||}. Syntax of P-terms: P ::= –P | (P1 AND P2) | (P1 OR P2) | L SOME C | L EACH C | (L V) | (L c), – – P≡P. Semantics of P-terms: || – P||(x) ó ך (||P||(x)), ||P1 AND P2||(x) ó ||P1||(x) ∧ ||P2||(x), ||P1 OR P2||(x) ó ||P1||(x) ∨ ||P2||(x), ||L SOME C||(x) ó$y ||L EACH C|| ó "y ||(L V)|| (x) ó (x, ||V||) ∈ ||L||, ||(L c)||(x) ó (x, ||c||) ∈ ||L||. Note that the expression L SOME D is a C-term or P-term depending on a context (position in the statement). Syntax of statements: S ::= – S | EACH C P | SOME C P | C1 ISA C2 | C1=C2 | L1= L2 | EXIST C | EXIST L | NULL C | NULL L, – – S≡S. Semantics of statements: || – S|| ó ך ||S||, ||EACH C P|| ó "yÎ||C||.||P||, ||SOME C P|| ó ||C1 ISA C2|| ó ||C1|| ⊆ ||C2||, ||C1=C2|| ó ||C1|| = ||C2||, ||EXIST C|| ó ||C||≠Æ, ||EXIST L|| ó ||L|| ≠Æ. The following expressions are considered as patterns for generating so-called primitive statements. A particular primitive statement is obtained from a pattern by replacing its variables with names from Cname and Iname. C1= – C2, EXIST C, EXIST L, NULL C, NULL L, C1 ISA C2, L1 ISA L2, C1=C2, L1=L2, C=C1 AND C2, C=C1 OR C2, L=L1 AND L2, L=L1 OR L2, C=C1 THAT P, C=L SOME C1, C=L1 ONLY C1, L=INV (L1), P= –P1, P=P1 AND P2, P=P1 OR P2, P=L SOME C, P=L EACH C, P=(L V), P (L c). One can transform every LLS-0 statement into the set of primitive statements. We show it by an example. Example 5. Let us take the statement (7) i.e. EXIST Animal THAT Eat SOME Animal THAT Eat EACH Grain and denote P1=Eat EACH Grain, C1=Animal THAT Eat EACH Grain, P2=Eat SOME Animal THAT Eat EACH Grain, C2=Animal THAT Eat SOME Animal THAT Eat EACH Grain. Then (7) is equivalent to conjunction of the following statements: P1=Eat EACH Grain, C1=Animal THAT P1, P2=Eat SOME C1, C2=Animal THAT P2, EXIST C2. Let O2 denote this set of five statements, and let O-st* denote the translation of the ontology O-st into primitive statements. Language LP. Every production has the antecedent and consequent.The antecedent and consequent of every (general) production are sequences of facts with parameters. With every pattern for primitive operator, it is associated a set of general productions. We will give some of them. 1. Pattern C1= – C2. +X IN C1 => -X IN C2, -X IN C1 => -X IN C2, +X IN C2 => -X IN C1, -X IN C2 => -X IN C1. 2. Pattern EXIST C. => +c IN C, +X IN C => EXIST С. 3. Pattern NULL C. => -x IN C, -x IN C => NULL С. 4. Pattern C1 ISA C2. +X IN C1 => +X IN C2, -X IN C2 => -X IN C1. 5. Pattern C = C1 AND C2. +X IN C => +X IN C1; +X IN C2, –X IN C; +X IN C1 => –X IN C2, –X IN C; +X IN C2 => –X IN C, –X IN C1 => –X IN C, –X IN C2 => –X IN C. 6. Pattern C = C1 THAT P. +X IN C => +X IN C1; +X IN P, –X IN C; +X IN C1 => –X IN P, –X IN C; +X IN P => –X IN C, –X IN C1 => –X IN C, –X IN P => –X IN C. 7. Pattern C = L SOME C1. +X1 L X2 => +X1 IN C; +X2 IN C1, +X IN C; +X1 L X2 => +X2 IN C1, +X IN C => –X IN c; c IN C2, –X IN C => –X L x, –X IN C1 => –x L X. Particular productions is obtained from general productions by replacing parameters with names from Cname and Iname. For example, consider the statement Wolf ISA Animal that has the pattern С1 ISA C2. Two general productions are associated with this pattern: +X IN C1 Þ +X IN C2, -X IN C2 Þ -X IN C1. Therefore the following two particular productions are associated with the statement Wolf ISA Animal: +X IN WolfÞ+X IN Animal, -X IN AnimalÞ -X IN Wolf. Let O be an ontology consisting of primitive statement. By Prod(O) we denote the set of productions associated with the statements from O. In particular, we have the set of productions Prod(O-st* U O2). In BMK there is the interpreter realizing the tactic of parallel execution of productions. One can apply the interpreter to solve the Steamroller problem. Process of application of productions begins with empty fact base B0 – the initial state of the ontology O-st*U O2. In the state B0 only the productions with the pattern EXIST C are applicable. As the result of their application we obtain the state B1={+c1 IN Wolf, +c2 IN Fox, +c3 IN Bird, +c4 IN Caterpillar, +c5 IN Snail, +c6 IN Grain}. In the state B1 only the productions with the pattern C1 ISA C2 are applicable. As the result of their application we obtain the state B2=В1 U {+ci IN Animal | 1 ≤i≤6}. Continuing further we will come to the state which contains the fact +c3(С2). Applying the production +X IN C Þ EXIST С to this fact we obtains the statement EXIST С2 and the statement EXIST Animal THAT Еat SOME Animal THAT Eat EACH Grain.
About use of BMK in designing intelligent transportation systems Last time ontologies have found applications to design intelligent information systems (ITS) [4]. Various information systems using ontologies are usually included in ITS. When a user works with ITS he needs to address to such subsystems. For example, if the user is interested in a given transport accident then he will probably want to know details about type of vehicles, road type, drivers, weather conditions etc. This particular information is compared with general information containing in several ontologies. If a driver wishes to find an optimal route to the given point then he can address to the subsystem of routing which will use the facts structured by the ontology for road networks. The facts represent information on current state of the road network, in particular, stream density on branches of the networks, places of road accidents, movement overlapping, roadwork, jams etc. The base of these facts can be considered as a state (an instance) of the ontology. Here we consider possibility to apply KMB ontologies to the problem of forecasting road jams. Let us take the following small fragment of the KBM ontology O-rf concerning the road traffic. Road[Name: String, Road_element(*), Junction(*), Picture: JPEG]. (8) Road_element[Number: Integer, Begin: Junction, End:Junction, Length: Integer, Lane(*), Average_vehicle_speed: Integer, Max_total_weight_allowed: Integer, Kind_of_movement: {one-way, two-way}, Capacity: Real, Belong_to: Street(0,1)]. Street[Name: String, Road_element(*)]. Road_net[Road_element(*), Picture: JPEG]. Assignment[Road_element/KEY, Flow_density: Real, Ball:{0...10}, Week_day: {mon, tue, wed, thu, fri, sut, sun}, Is_there_jam: Boolean]. State_of_road_net[Assignment(*)]. Junction[First_street: Street, Second_street: Street]. (State_of_road_net Close_to State_of_road_net) [Closeness_degree:Real]. The ontology O-rf can be used for the solution of a problem of forecasting of jams by case-based theory reasoning [5]. We consider the class Case as a subclass of the class State: Case[Time: Time]ISA State_of_road_net. Due this statement the class Case inherits all attributes and components of the class State_of_road_net. Suppose that a driver is on the street A once behind the intersection with the street B, and he is interested in knowing possibility of a jam on the street A before its intersection with the street C. The surrogate denoting the corresponding road element of the street A can be found by the following query: Q1:?X – X IN Road_element(Belong_to.Name= B); Begin.(First-street.Name= A; Second_street.Name= A); End.(First-street.Name= C; Second_street.Name= A). Let nei(X) (neighborhood of X) denote the function that for any road element X returns the set of all road elements at distance ≤ 2. This function can be defined as following: FUN nei: Road_element -> Road_element(*) nei(Х):={Y|Х.End=Y.Begin OR Х.End=Z.Begin; Z.End=Y.Begin}. END Consider the query Q2: ?MAX{Z.Closeness_degree} – (9) CURR(State_of_road_net/nei(ANS(Q1)); (Х Close_to Z Y); Y IN Case(Road_net IN nei(ANS(Q1)); Week_day= fri; Time£11:00; Time³10:00; Is_there_jam=true). Here ANS(Q1) denotes the answer to the query Q1. The record (9) denotes the state of the road net restricted to the neighborhood nei(ANS(Q1)) at the time the user addresses the interpreter with the query Q2. The answer to the query Q2 is the maximum value of the attribute Closeness_degree measuring degree of closeness of the current state to those cases in which a jam was observed at the time interval from 10 o’clock to 11 o’clock on Friday. The answer ANS(Q2) gives for the user a forecast of a jam in this situation. Conclusion We have described briefly the system “Binary Model of Knowledge” intended for specifying and interpreting ontologies. The description was made for a case of crisp ontologies. But it is possible to expand the BMK functionalities so to capture a case of fuzzy ontologies. In particular, it is possible to apply to KBM the techniques developed in [6] for interpreting fuzzy (flexible) conjunctive queries.
References 1. OWL 2 Web Ontology Language. Overview (2nd ed.). W3C Recommendation 11 December 2012. Available at: http://www.w3.org/TR/2012/REC-owl2-overview-20121211/ (accessed 15 December 2013). 2. Baader F., Calvanese D., McGuinness D., Nardi D., Patel-Schneider P. The Description Logic Handbook: theory, implementation and applications. Cambridge Univ. Press, 2nd ed., 2007. 3. Cardelli L. Type systems. In: Handbook of Computer Science and Engineering. CRC Press, 1997. 4. Ontology of transportation networks. REWERSE (reasoning on the Web with rules and semantics). A1-D4, 2005. 5. Kolodner J. An introduction to case-based reasoning. Artificial Intelligence Review, 1992, vol. 6, no. 1, pp. 3–34. 6. Pivert O., Bosc P. Fuzzy preference queries to relational databases, Imperial Coledge Press, 2012. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=3762&lang= |
Версия для печати Выпуск в формате PDF (7.83Мб) Скачать обложку в формате PDF (1.01Мб) |
| Статья опубликована в выпуске журнала № 1 за 2014 год. [ на стр. 76-81 ] |
Назад, к списку статей



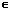 Surr},
Surr}, yÎ||C||.||P||,
yÎ||C||.||P||,