Построение методологии разработки моделей алгоритмов и процедур технологий кодирования и декодирования информации в задачах упаковки, защиты, восстановления и анализа больших потоков данных произвольного формата в каналах передачи и хранения информационных сетей и систем является актуальной и насущной проблемой современного информационного сообщества. Практическая реализация обозначенных технологий предполагает создание программных продуктов на основе моделей активной памяти как одного из наиболее эффективных и возможных способов кодирования и декодирования информации в каналах передачи и хранения.
Основные особенности разрабатываемых программных компонентов информационных технологий кодирования и декодирования информационных объектов (IO) на основе модели активной памяти могут быть обозначены и сформулированы следующим образом. Во-первых, логические схемы алгоритмов обозначенных технологий интерпретируют любой IO как бинарное информационное множество на логическом и физическом уровнях. Во-вторых, модели взаимодействия приемников и передатчиков данных в каналах передачи и способы логической организации данных в физической среде каналов хранения информационных и вычислительных систем рассматриваются и интерпретируются как функциональные атрибуты в процессах передачи и хранения информации соответствующих систем. В-третьих, физическая и логическая среда на разных уровнях иерархии памяти каналов передачи данных реальных компьютерных систем и сетей представляется как система виртуальной реальности, в которой реализуется независимая виртуализация физического пространства памяти каналов хранения и передачи в виде модели активной памяти [1].
Содержание и смысл основной посылки парадигмы моделей активной памяти в различных способах ее реализации в том, что она позволяет реализовать такие программные системы, которые обеспечивают пространственно-временную локальность и геторогенность IO в каналах передачи и хранения информации реальных информационных и вычислительных систем и сетей. Локальность в этом случае проявляется в том, что IO в каналах передачи и хранения имеют высокий уровень защиты и конфиденциальности в локальной пространственно-временной области информационного пространства памяти каналов систем и сетей без использования предлагаемых рынком информационных технологий программных продуктов защиты и архивации информации. Геторогенность или неоднородность IO проявляется в том, что IO в каналах передачи имеет свои механизмы криптографической защиты, реализуемые на основе моделей активной памяти в виде технологий виртуализации каналов [1].
Постановка задачи и способы ее решения. Постановка задачи практической реализации моделей активной памяти в данной работе рассматривается как результат логических схем построения моделей алгоритмов и процедур технологий кодирования и декодирования информации для задач упаковки, защиты, восстановления и анализа файловых структур произвольного формата в каналах передачи и хранения [1]. В качестве исходных информационных объектов для верификации разработанных программных продуктов и проведения анализа получаемых на их основе результатов были выбраны файлы различных форматов: TXT, BMP, WAV, EXE и EXE, заархивированный с помощью RAR.
Целевая установка состояла в следующем: во-первых, в рамках первой конфигурации информационного пространства реализовать информационные технологии упаковки файлов на основе префиксных методов Хаффмена и Шеннона–Фано и определить оптимальное информа- ционное пространство, в котором технология упаковки наиболее результативна. Во-вторых, определить закономерности между емкостными и информационными атрибутами файловых структур на бинарных полях в технологиях кодирования. В-третьих, провести сравнительный анализ практической эффективности относительно программных продуктов аналогичного характера.
В качестве емкостного атрибута в технологиях кодирования на бинарных полях выбран коэффициент сжатия Ксж, определяемый следующим выражением:
Ксж=Vвх/Vвых, (1)
где Vвх – объем файла, выраженный в битах, до кодирования; Vвых – объем файла после кодирования. Информационный атрибут задан в виде шенноновской энтропии на бинарном поле и вычисляется по формуле
I=– (2)
(2)
где pi – вероятность появления i-го символа (бинарной цепочки) алфавита N в представлении IO на бинарном поле.
 Файл до кодирования (исходный файл) емкостью Vвх как IO на бинарном поле определяется и описывается информационным пространством , где N – множество бинарных цепочек фиксированной длины, а после кодирования, но уже емкостью Vвых, – , где N1 – множество бинарных цепочек переменной длины. Для конкретного типа файла определялось оптимальное информационное пространство на множестве , где в качестве индексной переменной выступало N. В этом случае длина бинарной цепочки l (как мера образа символа алфавита N) выступала и являлась независимой переменной, относительно которой рассчитывались оценки емкостных и информационных атрибутов. Оценки обозначенных атрибутов вычислялись для компонентов заголовка и информационной части кодируемого файла для различных значений l, и строились графические зависимости атрибутов как функций от l. Для различных форматов файлов определялись следующие формулы оценки емкостных атрибутов как функций аргумента l:
Файл до кодирования (исходный файл) емкостью Vвх как IO на бинарном поле определяется и описывается информационным пространством , где N – множество бинарных цепочек фиксированной длины, а после кодирования, но уже емкостью Vвых, – , где N1 – множество бинарных цепочек переменной длины. Для конкретного типа файла определялось оптимальное информационное пространство на множестве , где в качестве индексной переменной выступало N. В этом случае длина бинарной цепочки l (как мера образа символа алфавита N) выступала и являлась независимой переменной, относительно которой рассчитывались оценки емкостных и информационных атрибутов. Оценки обозначенных атрибутов вычислялись для компонентов заголовка и информационной части кодируемого файла для различных значений l, и строились графические зависимости атрибутов как функций от l. Для различных форматов файлов определялись следующие формулы оценки емкостных атрибутов как функций аргумента l:
K1(l)=Vsl/Vвх, (3)
где Vsl=VN+VN1 – объем словаря, VN и VN1 – соответственно объемы алфавитов N и N1 при фиксированном значении l. Оценка для Kсж(l) опреде- лялась по формуле (1). Для третьего емкостного атрибута оценка определялась следующим выражением:
K2(l)=VN1/VN. (4)
В качестве информационных атрибутов рассматривались Imax(l) – максимальная шенноновская энтропия кодируемого файла и I(l) – реальная энтропия, оценки для которых при различных значениях l вычислялись по формуле (2).
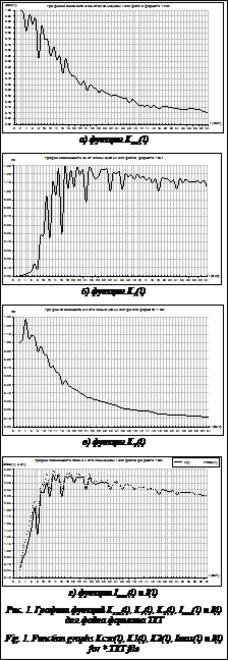
Практическая реализация. Полученные результаты отражены в виде графиков функций Kсж(l), K1(l), K2(l), Imax(l), I(l) для кодируемых файлов различных форматов. На рисунке 1 приведены графики этих функций для кодируемого файла формата TXT с нерегулярной структурой. Для функции Kсж(l) (см. рис. 1а) на интервале lÎ(2÷64) ее размах достигает одного порядка, то есть на этом интервале определены основные оптимальные значения для емкостных атрибутов.
На рисунке 1б показан график функции K1(l), отражающей динамику отношения объема словаря к объему кодируемого файла. Видно, что с увеличением l до 32 бит происходят резкие изменения функции в точках, кратных байту и полубайту, то есть это свойство функции-атрибута указывает на то, что единицей информационного квантования файлов такого формата на бинарных полях является бинарная цепочка, кратная байту. И на таких длинах цепочек заключены значения l для определения оптимального информационного пространства.
График функции K2(l) показан на рисунке 1в, где отражена динамика отношения объемов алфавитов N и N1 при различных значениях l. Характер такой динамики аналогичен динамике функции Kсж(l), но с меньшим затуханием.
На рисунке 1г приведены графики функций Imax(l) и I(l), которые отражают основные свойства информационных характеристик кодируемого файла – оптимальные значения l находятся в точках, где энтропия минимальна, то есть в этом случае проявляется высокая корреляция емкостных и информационных атрибутов файла.
На рисунке 2 приведены графики аналогичных функций для кодируемого файла формата EXE. Функция Kсж(l) (см. рис. 2а) на рассматриваемом интервале изменения l имеет размах в пределах одного порядка, но общая шкала вдвое меньше, чем для аналогичной функции файла формата TXT (см. рис. 1а). Характер поведения функции на всем интервале изменения l более гладкий относительно четных и нечетных значений l.
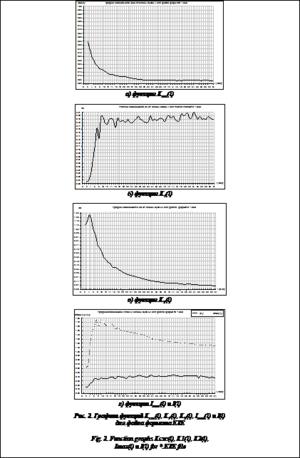 График функции K1(l) (см. рис. 2б) отражает нерегулярные свойства файла данного формата как IO на бинарном поле в информационном пространстве для любого N с ростом четных и нечетных значений l. Общая шкала изменения функции более чем в шесть раз меньше относительно аналогичной функции файла формата TXT (см. рис. 1б). Это обстоятельство, хотя и в скрытой форме, подтверждает характер нерегулярной структуры файла такого формата в информационном пространстве.
График функции K1(l) (см. рис. 2б) отражает нерегулярные свойства файла данного формата как IO на бинарном поле в информационном пространстве для любого N с ростом четных и нечетных значений l. Общая шкала изменения функции более чем в шесть раз меньше относительно аналогичной функции файла формата TXT (см. рис. 1б). Это обстоятельство, хотя и в скрытой форме, подтверждает характер нерегулярной структуры файла такого формата в информационном пространстве.
На рисунке 2в показан график функции K2(l), поведение которой аналогично такой же функции файла формата TXT (см. рис. 1в), но обладающей более гладкими свойствами. Приведенные графики функций Imax(l) и I(l) на рисунке 2г отражают свойства информационных характеристик кодируемого файла формата EXE: Imax(l) отражает и описывает степень однородности или регулярности IO в информационном пространстве , когда все символы N в рассматриваемом файле равновероятны при любых значениях l; I(l) отражает и описывает реальный уровень однородности или регулярности рассматриваемого файла. Как видно из визуального сравнения, на рассматриваемом интервале изменений l различия между функциями Imax(l) и I(l) проявляются в количественном и качественном отношениях, то есть в этом случае корреляция емкостных и информационных атрибутов файла не происходит.
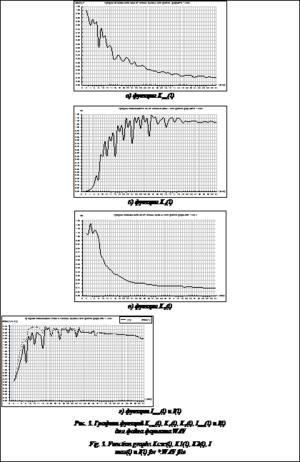
Графики функций Kсж(l), K1(l), K2(l), Imax(l), I(l) для кодируемого файла формата WAV приведены на рисунке 3. График функции Kсж(l) (рис. 3а) во многом отражает свойства аналогичной функции для файла формата TXT. Видно, что резкие изменения функции происходят в пределах изменения l от 0 до 16 бит в точках, кратных байту и полубайту, указывая на то, что информационным квантом файла такого формата является бинарная цепочка, не превышающая двух байтов.
График функции K1(l) (рис. 3б) показывает, что с увеличением l до 32 бит происходят резкие изменения функции в точках, кратных байту и полубайту. Это свойство данной функции-атрибута файла указывает на то, что логическая органи- зация файла такого формата на бинарном поле образует регулярную структуру в информационном пространстве при отмеченных значениях l.
График функции K2(l) (рис. 3в) во многом отражает характер поведения аналогичной функции Kсж(l), но с меньшим и более гладким затуханием.
Приведенные на рисунке 3г графики функций Imax(l) и I(l), с одной стороны, отражают основные свойства емкостных и информационных харак- теристик кодируемого файла: оптимальные зна- чения l находятся в точках, где энтропия минимальна, а с другой – указывают на регулярную структуру логической организации файла, проявляющуюся в высокой корреляции емкостных и информационных атрибутов файла.
 Приведенные результаты исследований, представленные в виде графиков емкостных и информационных атрибутов файлов как функций от переменной l, позволяют сделать следующие выводы и обобщения. Во-первых, можно описать любой IO и отразить его основные свойства и характеристики посредством емкостных и информационных атрибутов в информационном пространстве, определенном на бинарном поле. Во-вторых, каждый IO в каналах передачи и хранения информационных систем обладает уникальным набором значений емкостных и информационных атри- бутов, посредством которых можно адекватно идентифицировать его как уникальный объект. В-третьих, емкостные и информационные атрибуты являются теми математическими сущностями, посредством которых задачи упаковки, защиты, восстановления и анализа файловых структур произвольного формата в каналах передачи и хранения формализуются и решаются на физическом и логическом уровнях.
Приведенные результаты исследований, представленные в виде графиков емкостных и информационных атрибутов файлов как функций от переменной l, позволяют сделать следующие выводы и обобщения. Во-первых, можно описать любой IO и отразить его основные свойства и характеристики посредством емкостных и информационных атрибутов в информационном пространстве, определенном на бинарном поле. Во-вторых, каждый IO в каналах передачи и хранения информационных систем обладает уникальным набором значений емкостных и информационных атри- бутов, посредством которых можно адекватно идентифицировать его как уникальный объект. В-третьих, емкостные и информационные атрибуты являются теми математическими сущностями, посредством которых задачи упаковки, защиты, восстановления и анализа файловых структур произвольного формата в каналах передачи и хранения формализуются и решаются на физическом и логическом уровнях.
Сравнительный анализ практической эффективности разрабатываемого подхода относительно программных продуктов типа RAR, ZIP и других, ориентированных на решение аналогичных задач, выявил следующие особенности и закономерности:
1) программные продукты, доступные на рынке информационных технологий для решения обозначенных задач, имеют иную математическую и логическую основу – они привязаны к логической структуре форматов файлов, их статистическим характеристикам или другим особенностям;
2) логические схемы таких технологий просты и не защищены в смысле разработки математически осмысленных моделей алгоритмов и процедур кодеров и декодеров.
Количественные оценки эффективности разработанных программных продуктов упаковки рассмотренных выше форматов файлов относительно архиваторов типа RAR, ZIP и других и сравнительный анализ с результатами других исследователей [2–4] показали, что разработка технологий упаковки на основе моделей активной памяти IO дает результаты, намного лучшие (для форматов файлов, приведенных здесь, в пределах порядка), чем при использовании для аналогичных целей традиционных и устоявшихся схем.
На основе анализа полученных результатов кратко сформулируем основные положения и выводы относительно парадигмы о практической реализации моделей активной памяти для решения задач упаковки, защиты, восстановления и анализа больших потоков данных произвольного формата в каналах передачи и хранения информационных сетей и систем в виде технологий виртуализации их каналов передачи и хранения. Во-первых, модели активной памяти в технологиях кодирования и декодирования IO на бинарных полях в задачах передачи, хранения и защиты для каналов информационных систем позволяют повысить инвариантную защищенность IO относительно как средств передачи и хранения, так и способов размещения их в информационной таре файловых структур любой природы и физической среды. Это означает, что такие модели дают оптимальный одинаковый эффект как по архивации и сжатию IO, так и по защищенности их в любой физической и информационной среде с точностью до бинарного отображения IO в ней, а образы логических структур IO в виртуальной памяти каналов передачи и хранения обладают информационной связанностью. Во-вторых, модели активной памяти на бинарных полях являются новым способом разработки и практической реализации технологий виртуализации IO в каналах хранения и передачи и информационных, и компьютерных систем, но уже на новом качественном и количественном уровнях их практической реализации в технологиях кодирования и декодирования информации в задачах упаковки, защиты, восстановления и анализа потоков данных для решения широкого класса прикладных задач. В этом случае модели активной памяти для их практической реализации образуют математическую и логическую основу при создании технологий виртуализации каналов хранения и передачи информационных систем с произвольной архитектурой, топологией и организацией связей.
Литература
1. Мышев А.В. Модели активной памяти в технологиях виртуализации каналов передачи и хранения информации // Программные продукты и системы. 2010. № 1. С. 54–58.
2. Красильников Н.Н. Методы увеличения сжатия изображений энтропийными кодерами // Информационно-управляющие системы. 2004. № 1. С. 10–13.
3. Семенюк В.В. Экономное кодирование дискретной информации. СПб: Изд-во СПб ГИТМО(ТУ), 2001. 115 с.
4. Ватолин Д., Ратушняк А., Смирнов М., Юркин В. Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео. М.: Диалог-МИФИ, 2002. 384 с.
Referens
1. Myshev A.V. Active memory models on binary fields in virtualization technologies of data transmission and storage channels. Programmnye produkty i sistemy [Software & Systems]. 2010, no. 1, pp. 54–58 (in Russ.).
2. Krasilnikov N.N. Methods for increasing image compression using entropy coders. Informatsionno-upravlyayushchie sistemy [Information and Control Systems]. 2004, no. 1, pp. 10–13.
3. Semenyuk V.V. Ekonomnoe kodirovanie diskretnoy informatsii [Economical discrete data coding]. St. Petersburg, St. Petersburg State Univ. of Information Technologies, Mechanics and Optics. 2001, 115 p.
4. Vatolin D., Ratushnyak A., Smirnov M., Yurkin V. Metody szhatiya dannykh. Ustroystvo arkhivatorov, szhatie izobrazheniy i video [Methods for data compression. Archivers organization, image and video compression]. Moscow, Dialog-MIFI Publ., 2002, 384 p.



 (2)
(2)


