Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: Matveev, Yu.N. (matveev4700@mail.ru) - Tver State Technical University (Professor), Tver, Russia, Ph.D, () - | |
| Ключевое слово: |
|
| Page views: 9266 |
Print version Full issue in PDF (1.17Mb) |
Вот уже несколько десятилетий тенденция к использованию имитационного моделирования вместо реального (физического) эксперимента носит прогрессирующий характер. Это обусловлено как экономической целесообразностью, так и невозможностью построения моделей и проведения эксперимента над некоторыми объектами реального мира. К классу сложных систем относятся также компьютерные тренажерные системы и комплексы. Построение адекватной модели в таких системах играет очень важную роль. Реальная компьютерная тренажерная система
При заданных параметрах Моделью
При заданных параметрах Все реальные системы Пусть имеются некоторые целевые функционалы
и совокупности параметров Систему Решение экстремальных задач приводит к зависимостям:
из которых следует, что оптимальные система Имеется два принципиально антагонистичных подхода в выборе моделей Первый подход (аналитический) состоит в приближении модели Второй подход (синтетический) рассматривает лишь реальные системы Аналитический и синтетический подходы используют модели При моделировании реальных компьютерных тренажерных систем, носящих зачастую распределенный характер, наиболее применим синтетический подход, уже хотя бы потому, что приближение N к N*, а L к L* если и возможно, то достаточно ресурсоемко. |
| Permanent link: http://swsys.ru/index.php?page=article&id=400&lang=en |
Print version Full issue in PDF (1.17Mb) |
| The article was published in issue no. № 2, 2007 |
Perhaps, you might be interested in the following articles of similar topics:
- Формулировка задачи планирования линейных и циклических участков кода
- Прототип интеллектуальной системы поддержки принятия решений для управления энергообъектом
- Оптимизация обработки информационных запросов в СУБД
- Учебно-исследовательский программно-лабораторный комплекс NET_LAB
- Система автоматизации процессов рабочего проектирования сложного изделия
Back to the list of articles
 в общем случае может быть описана большим числом
в общем случае может быть описана большим числом 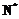 параметров
параметров 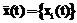 , где
, где 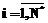 , зависящих от времени
, зависящих от времени 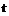 (другими словами,
(другими словами,  зависимостями между ними:
зависимостями между ними: , где
, где  . (1)
. (1)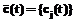 система имеет
система имеет 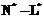 степеней свободы (или независимых параметров).
степеней свободы (или независимых параметров).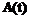 реальной системы
реальной системы 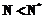 параметрами
параметрами 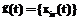 , где
, где  с учетом лишь
с учетом лишь  зависимостей:
зависимостей: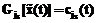 , где
, где 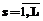 . (2)
. (2) модель имеет
модель имеет 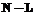 степеней свободы. Точки
степеней свободы. Точки 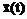 и
и  с ростом
с ростом 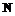 к
к 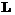 к
к 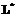 , тем меньше «рассогласование» этих траекторий, измеряемое любой естественной мерой, например максимумом модуля разности соответствующих координат.
, тем меньше «рассогласование» этих траекторий, измеряемое любой естественной мерой, например максимумом модуля разности соответствующих координат. .
.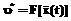 и
и 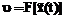 (3)
(3)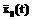 и
и 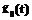 обращают их в экстремумы (максимумы или минимумы в зависимости от их смысла) при условиях (1) и (2) соответственно.
обращают их в экстремумы (максимумы или минимумы в зависимости от их смысла) при условиях (1) и (2) соответственно.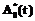 и модель
и модель 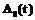 , которые будут соответствовать экстремальным значениям параметров, можно назвать оптимальными.
, которые будут соответствовать экстремальным значениям параметров, можно назвать оптимальными.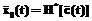 и
и 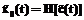 ,
,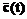 и
и 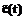 имеют
имеют 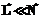 можно сказать, что
можно сказать, что 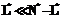 и требуемая адекватность выглядит реальнее достижимой для синтетического подхода, чем для аналитического (реальнее возможность преодоления ситуаций, связанных с системами, имеющими большое количество параметров). Однако использование второго подхода по сравнению с первым усложнено введением параметра оптимальности.
и требуемая адекватность выглядит реальнее достижимой для синтетического подхода, чем для аналитического (реальнее возможность преодоления ситуаций, связанных с системами, имеющими большое количество параметров). Однако использование второго подхода по сравнению с первым усложнено введением параметра оптимальности.