Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Распределенная подпись RSA
Аннотация:
Abstract:
| Автор: Фомин А.Д. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 9498 |
Версия для печати Выпуск в формате PDF (1.17Мб) |
Данная работа посвящена распределенной схеме подписи RSA, которая определяется процедурой разделения секретного ключа RSA среди участников системы и процедурой совместной постановки подписи подгруппой участников. Одним из важнейших свойств распределенных схем подписи является отсутствие интерактивности процедуры выдачи новой проекции без дилера. Для интерактивного протокола предполагается обмен данными между действующими участниками, что является существенным недостатком, так как растет объем трафика в системе, повышается расход энергии и требуется синхронизация действий узлов. Другим важным свойством распределенных схем подписи является возможность независимой работы участников коалиции при постановке подписи. Данное свойство при изменении состава участников коалиции позволяет не перезапускать протокол постановки подписи, что приводит к сокращению задержки при постановке подписи. Еще одним свойством распределенных схем подписи является возможность самоорганизации, то есть должна быть предусмотрена возможность работы системы без участия дилера после этапа инициализации. В существующих работах, посвященных распределенной подписи RSA, можно выделить три основных подхода к распределению секретного ключа RSA. При первом подходе подразумевается, что секретный ключ При втором подходе предполагается наличие дополнительного уровня в схеме разделения секрета. При этом сначала секрет разделяется между n узлами аддитивно, а потом каждая полученная проекция распределяется при помощи пороговой схемы. Подобные схемы интерактивны и неработоспособны без дилера. При третьем подходе предполагается разделение секретного ключа d над известным кольцом Таким образом, каждая из упомянутых ранее схем имеет некоторые функциональные ограничения и не отвечает по крайней мере одному из следующих требований: - процедура постановки подписи должна обеспечивать независимость действий участников коалиции; - система должна обладать свойством самоорганизации, то есть после инициализации не нуждаться в участии дилера; - процедура выдачи проекции секрета без дилера должна быть неинтерактивна. В большинстве известных работ рассматривается схема разделения секрета Шамира. В схеме Шамира предполагается заданным полином Чтобы использовать схему Шамира для распределенной подписи RSA, необходимо выбрать секрет S и модуль P. Для распределенной подписи RSA секретом является секретный ключ d. Относительно модуля P имеется две возможности: либо сделать его публичным, например P=N, либо секретным, положив Опишем схему разделения секрета, для которой процедура выдачи проекции без дилера становится неинтерактивной, а размер проекции секретного ключа, используемой для постановки подписи, не превышает Введем в рассмотрение простое число
При таком задании функции разделения секрета нельзя использовать интерполяцию по Лагранжу. Вместо этого необходимо решать систему линейных уравнений. Для восстановления секрета каждый участник коалиции u вычисляет значение своей функции в точке x=0, получая
Для выдачи проекции новому участнику без дилера каждый участник коалиции u вычисляет значение своей функции в точке
На основе описанной модифицированной схемы разделения секрета можно предложить следующую схему распределенной подписи RSA. 1. Инициализация схемы. (a) Дилер генерирует простое число (b) Дилер генерирует публичный ключ RSA (c) Дилер генерирует функцию
(d) Каждый узел u в качестве проекции секретного ключа получает функцию 2. Распределенная постановка подписи. (a) Выбирается коалиция K из t участников. Каждый участник коалиции вычисляет частичную подпись по формуле (b) После получения t частичных подписей сборщик подписи составляет матрицу G для членов коалиции K и обращает ее над полем рациональных чисел. (c) Сборщик подписи вычисляет (d) Используя матрицу
(e) Сборщик находит x,y такие, что (f) Подпись вычисляется как 3. Выдача проекции ключа новому узлу. (a) Для получения проекции секретного ключа новый узел u должен найти коалицию K из t уже проинициализированных узлов и сообщить им свое (b) Каждый участник коалиции u вычисляет значение своей функции в точке (c) Новый узел находит свою проекцию секрета
Таким образом, выдача проекции секретного ключа новому узлу не требует участия дилера и является неинтерактивной. В заключение отметим, что предложенная схема распределенной подписи RSA обладает следующими достоинствами: действия участников коалиции при постановке подписи независимы, протокол выдачи проекций секретного ключа неинтерактивен и не требует участия дилера после инициализации системы. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=401 |
Версия для печати Выпуск в формате PDF (1.17Мб) |
| Статья опубликована в выпуске журнала № 2 за 2007 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Две задачи, в решение которых внес коррективы компьютер
- Разработка и сопровождение учебно-контролирующих программ для интернета в инструментальной среде ГИПЕРТЕСТ
- Методика экономической оценки потребительского качества программных средств
- Средства защиты информации в системе АРСОТ
- Диалоговая система поддержки моделей функционирования
Назад, к списку статей



 распределяется по схеме разделения секрета Шамира над кольцом
распределяется по схеме разделения секрета Шамира над кольцом 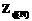 (или
(или 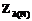 ), где
), где 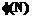 (или
(или 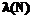 ) не опубликованы. Отсутствие информации о
) не опубликованы. Отсутствие информации о 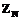 вместо
вместо 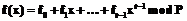 , в котором
, в котором 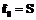 – секрет;
– секрет; 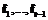 – случайные значения; P – простое число. Каждый участник протокола получает проекцию секрета в виде
– случайные значения; P – простое число. Каждый участник протокола получает проекцию секрета в виде 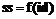 , где id – идентификатор участника. Любая коалиция K из t участников сможет восстановить секрет
, где id – идентификатор участника. Любая коалиция K из t участников сможет восстановить секрет 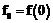 , используя интерполяцию по Лагранжу:
, используя интерполяцию по Лагранжу: 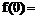
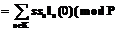 ), где
), где 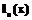 – коэффициенты Лагранжа.
– коэффициенты Лагранжа.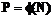 или
или 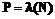 . Если P всем известно (например модуль RSA), это приведет к утечке информации и взаимозависимости действий участников коалиции во время выполнения процедуры постановки распределенной подписи. Если P – секретное значение (например
. Если P всем известно (например модуль RSA), это приведет к утечке информации и взаимозависимости действий участников коалиции во время выполнения процедуры постановки распределенной подписи. Если P – секретное значение (например 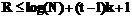 , где N –модуль RSA; t – размер коалиции; k – длина идентификатора узла.
, где N –модуль RSA; t – размер коалиции; k – длина идентификатора узла.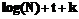 .
.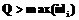 и будем вычислять проекции секрета по формуле:
и будем вычислять проекции секрета по формуле: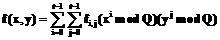 .
.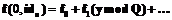
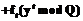 в точке
в точке 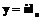 . При этом
. При этом 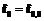 . Имея t значений данной функции, можно восстановить секрет, решив следующую систему уравнений:
. Имея t значений данной функции, можно восстановить секрет, решив следующую систему уравнений: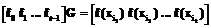 , где
, где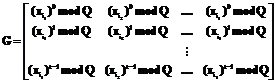 .
.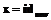 , получая
, получая 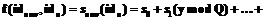
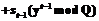 в точке
в точке 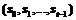 для нового абонента находится из системы уравнений:
для нового абонента находится из системы уравнений: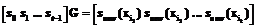 .
.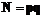 и
и 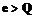 – простое число и вычисляет секретный ключ
– простое число и вычисляет секретный ключ 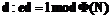 .
.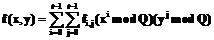 , где
, где 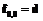 , а коэффициенты
, а коэффициенты 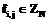 выбраны случайным образом с соблюдением условия
выбраны случайным образом с соблюдением условия 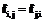 .
.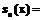
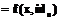 .
.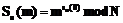 , где m – значение хэш-функции от подписываемого сообщения и
, где m – значение хэш-функции от подписываемого сообщения и 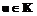 .
.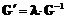 , где
, где 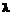 – наименьшее общее кратное знаменателей всех элементов матрицы
– наименьшее общее кратное знаменателей всех элементов матрицы 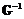 .
.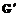 , он вычисляет:
, он вычисляет: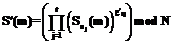 .
.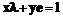 .
.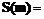
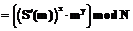 .
.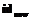 .
.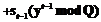 в точке
в точке 