Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Оптимизация процесса обнаружения орбит новых космических объектов с помощью параллельного расчета возможных орбит
Аннотация:Наблюдение и каталогизация малоразмерных объектов космического мусора в околоземном космическом пространстве требуют совершенствования применяемых методов и алгоритмов получения и обработки информации для повышения эффективности работы оптических средств. Один из подходов оперативного обнаружения и определения орбит некаталогизированных объектов космического мусора апробирован и успешно применяется на российских оптических наблюдательных наземных средствах. Однако много времени тратится на операцию полного перебора коротких серий измерений (треков) и выбор разнесенных во времени трех треков, предположительно, относящихся к одному объекту космического мусора и используемых для последующего построения возможной первоначальной орбиты. Данная статья посвящена вопросу сокращения перебора треков посредством предварительного анализа полученных измерений с помощью априорного построения границ изменения параметров возможных орбит. Вычисли-тельные эксперименты, проводимые в рамках исследования этой прикладной задачи, направлены на уменьшение средней скорости обработки одного трека при увеличении точности полученной оценки. Скорость обработки одного трека естественным образом ограничена, так как, являясь частью общей программы обработки траекторных измерений, построение оценки параметров возможных орбит для каждого трека не должно сильно влиять на общее время цикла обработки измерений. При этом уменьшение средней скорости обработки одного трека и одновременное повышение точности оценок становятся возможными при параллельной организации работы программы. Так, для оптимизации работы программы обнаружения и определения орбит новых космических объектов предлагается параллельный алгоритм построения границ изменения параметров возможных орбит для последующего выбора троек треков, допустимые области изменений параметров которых имеют непустое пересечение. Алгоритм реализован на языке Т++ для Т-системы с открытой архитектурой (OpenTS).
Abstract:Observation and cataloging of small debris objects in near–Earth space requires the improvement of the methods and algorithms for obtaining and processing information to improve the efficiency of the optical means. One of the approaches for operative detection of uncatalogued space debris objects orbits has been tested and used successfully in Russian optical observation ground facilities. However, much time is spent on the operation of the exhaustive search of short series of measurements (tracks) and the choice of three series separated in time, presumably belonging to the same object debris and used for the subsequent construction of a possible initial orbit. The article considers the issue of reducing tracks exhaustive search using preliminary analysis of the measurements by a priori constructing the boundaries of possible orbits parameters’ changes. Computational experiments within the research of this application problem are aimed at reducing the average processing speed of one track by increasing the accuracy of estimation. The processing speed of one track is naturally limited since the construction of the possible orbits parameter estimates for each track should not greatly affect the time of the overall measurement processing cycle as part of a trajectory measurements general processing program. The decrease in the average processing speed of one track and the simultaneous increasing the accuracy of estimates is possible with a parallel operation of the program. So, in order to optimize the program for detecting and determining the orbits of new space objects it is proposed to use a parallel algorithm for constructing the boundaries of the possible orbits changes for selection of allowable triples of tracks which have nonempty intersection. The algorithm is implemented in T++ for a T-system with an open architecture (OpenTS).
| Авторы: Трушкова Е.А. (katerinatr@mail.ru) - Институт проблем управления им. В.А. Трапезникова РАН, Москва, Россия, доктор физико-математических наук, Матвеев Г.А. (gera@prime.botik.ru) - Институт программных систем им. А.К. Айламазяна РАН (ведущий инженер-исследователь), Переславль-Залесский, Россия | |
| Ключевые слова: параллельное расширение си++, т-система, opents, язык программирования т++, динамическое распараллеливание, параллельный алгоритм, первоначальная орбита, околоземное космическое пространство, космический мусор |
|
| Keywords: с++parallel extension, t-system, opents, T++ programming language, dynamic parallelization, parallel algorithm, the initial orbit, near-Earth space, space debris |
|
| Количество просмотров: 7400 |
Версия для печати Выпуск в формате PDF (8.21Мб) Скачать обложку в формате PDF (1.09Мб) |
Основным направлением развития и применения оптико-электронных средств наблюдения космического пространства является расширение их возможностей по наблюдению, сопровождению и каталогизации малоразмерных объектов космического мусора (ОКМ) [1−5]. Примерами успешно развиваемых ключевых разработок в этом направлении являются сокращение временного цикла обзора одной площадки, применение эффективных стратегий обзора, оперативное обнаружение и определение орбит некаталогизированных ОКМ во время проведения сеанса наблюдений [6−8]. Одновременно с основным режимом работы обзорного средства работает и комплекс программ обработки траекторных измерений (ОТИ), осуществляющий оперативную обработку измерений для идентификации с орбитами каталогизированных космических объектов (КО). При успешной идентификации измерений комплекс программ ОТИ производит уточнение орбит каталогизированных КО по полученным измерениям. Если полученные измерения не идентифицировались ни с одним каталогизированным объектом, непосредственно в процессе наблюдений дополнительно решаются задачи обнаружения и сбора информации по некаталогизированному ОКМ. При получении очередной серии неидентифицированных измерений запускается задача определения орбит новых КО, которая заключается в поиске неидентифицированных измерений, относящихся к одному КО, построению и записи в каталог орбиты по этому КО. Один из подходов оперативного обнаружения и определения орбит некаталогизированных ОКМ апробирован и успешно применяется на российских оптических широкопольных средствах [1]. Однако много времени тратится на операцию полного перебора коротких серий измерений (треков) и выбор разнесенных во времени трех серий, предположительно, относящихся к одному КО, используемых для последующего построения возможной орбиты. Данная статья посвящена вопросу сокращения перебора треков при помощи предварительного анализа полученных измерений с точки зрения параллельного априорного построения границ изменения параметров возможных орбит. Подобный подход был использован в работе [9] для решения задачи идентификации орбиты с помощью генерации множества возможных орбит, построенных в параллельном режиме по имеющимся угловым измерениям от оптических наземных средств. Так, для ускорения работы программы обнаружения и определения орбит некаталогизированных ОКМ предлагается использовать вспомогательный алгоритм: строить для каждого трека допустимые области изменений трех параметров возможных орбит в виде пространственного параллелепипеда и затем выбирать только те тройки треков, соответствующие параллелепипеды для которых имеют непустое пересечение. Постановка задачи Для каждого трека (группы последовательных измерений) Ti данной последовательности треков
то есть границы изменения параметров возможных орбит для трех треков пересекаются (пересечение соответствующих параллелепипедов в пространстве изменения трех переменных (r, I, W) не пусто). Это позволяет в последовательности треков, переданных на обнаружение, существенно сократить количество перебираемых троек. Так, в нижеследующем примере для входящей последовательности из 13 треков (n=13) число полного перебора троек Основная задача состоит в нахождении по измерениям (время t, прямое восхождение a, склонение d, координаты измерительной станции R) одного трека Вспомогательные задачи Задача 1. Выбор из измерений трека двух «хороших». Для решения задачи значения aj и dj приближаются кривыми второго порядка a(t) и d(t) по методу наименьших квадратов. Из всех измерений данного трека выбираются два j1, j2, для которых расстояние между точкой трека (aj, dj) и ее аппроксимацией (a(tj), d(tj)) наименьшее, при условии, что |j1-j2| не меньше половины общего количества измерений. Далее, формально полагая j1=1, j2=2, выбранные измерения будем обозначать через Задача 2. По данным (a, d, R), [amin, amax], [emin, emax] осуществляется построение начальных границ дальности rÎ[r0min, r0max]. Искомые границы получаются как решение системы неравенств относительно неизвестного r (интервал между минимально допустимым перигеем и максимально допустимым апогеем): (amin(1-emax))2 £ ||r(r)||2 £ (amax(1+emax))2, r³0, где r(r)=R+ru, u=(cosd cosa, cosd sina, sind)T. Задача 3. По данным Искомые значения
где m − гравитационная постоянная; r = R + ru, u = (cosd cosa, cosd sina, sind)T;
После чего соответствующие значения e+ находятся по формуле (норма вектора Лапласа)
Основная задача При заданном значении точности e для сетки узловых значений a в области [amin, amax] при известных значениях Сначала решается задача 2 по данным (α1, δ1, R1) и (α2, δ2, R2) определяется область изменения дальностей [r1min, r1max] ´ [r2min, r2 max]. Далее осуществляется перебор узловых значений (a, ρ1, ρ2) по сетке в полученной области [amin, amax] ´ [r1min, r1max] ´ [r2min, r2max], а именно: для каждой тройки значений (a, ρ1, ρ2) выполняется следующее. · Проверяется выполнение условий (наименьший возможный эксцентриситет e0 и наименьшая возможная длина большой полуоси a0, а также теорема Эйлера о времени полета Dtp между данными точками положения на параболической (с нулевой энергией) орбите):
где r1 = R1 + r1u1, r2 = R2 + r2u2,
· Вычисляются значения I=arc cos(nk), · Решается задача 3 для наборов данных · Проверяется выполнение условий: |e1± - e2±| £ £e(emax - emin), |I - I±| £ 180e, |W - W±| £ 360e. · Вычисляются границы изменения параметров a, ρ, I, W «хороших» орбит. Дальнейшее уточнение полученных границ изменения возможных орбит может быть проведено итерационно для уменьшающегося на каждой итерации значения точности e. При этом на каждой последующей итерации в качестве начальных границ изменения дальности выбираются границы, полученные на предыдущей итерации. Соответствующая последовательность полученных границ изменения параметров орбит представляет в этом случае последовательность вложенных параллелепипедов в пространстве изменения трех переменных (ρ, I, W). Вычислительные эксперименты Входная последовательность включает 13 треков. После выбора в каждом треке двух измерений получены необходимые для вычисления границ параметров орбит данные (табл. 1). Полут т ченные границы орбит приведены в таблице 2 (выделены четыре области изменения эксцентриситета: earea=1 соответствует области 0£e£0,1, earea=2-0,1£ £e£0,3, earea=3-0,3£e£0,6 и earea=4-0,6£e£ 0,9). На рисунках 1 и 2 в виде проекций параллелепипедов на плоскости (I, W) и (ρ, W) соответственно представлены полученные границы орбит для каждого из треков в четвертой области изменения эксцентриситета (earea=4, то есть 0,6£e£0,9), так как именно эта область порождает максимальное количество допустимых троек треков. После анализа пересечений границ параметров возможных орбит по 13 трекам сформировалась последовательность всего из 13 троек треков: 1-5-7, 1-7-8, 2-3-4, 2-3-6, 2-4-6, 3-4-6, 4-6-10, 4-6-11, 4-10-11, 5-6-7, 5-6-12, 5-7-8, 6-10-11. Особенности программной реализации Вычислительные эксперименты направлены на уменьшение средней скорости обработки одного трека при увеличении точности полученной оценки, так как скорость обработки одного трека естественным образом ограничена. Предложено для четырех подобластей изменения эксцентриситета параллельно решать задачу для каждого трека. При этом для каждой подобласти и каждого трека число итераций, необходимых для достижения требуемой точности, заранее неизвестно. Следовательно, при дальнейшей программной реализации алгоритма заранее неизвестно, как будут загружены отдельные узлы вычислительной установки. Поэтому динамические программы предпочтительнее любых других типов. Динамическое распараллеливание имеет ряд преимуществ не только для случая, когда вопросы организации параллельного счета решаются во время исполнения программы, но и для выравнивания нагрузки в гетерогенных и/или меняющихся со временем параллельных вычислительных системах, а также для задач, обладающих гранулами различной тяжести. При этом использование неявных конструкций распараллеливания вычислений позволяет легко переносить программы между различными платформами параллельных вычислений – многопроцессорными системами, вычислительными кластерами, метакластерными системами и т.п. Т-система (OpenTS) – система параллельного программирования, реализующая концепцию автоматического динамического распараллеливания программ. Это оригинальная российская разработка, которая ведется в Институте программных систем им. А.К. Айламазяна РАН [10, 11], представляющая систему параллельного программирования, реализующую концепцию автоматического динамического распараллеливания программ. То есть многие аспекты организации параллельного счета (распределение задач по узлам кластера, синхронизация процессов, организация пересылки данных) выполняются не программистом, а самой системой. Во многих случаях Т-системе удается удачно организовать все эти виды работ и получить хороший уровень распараллеливания программ. Язык T++ является входным языком Т-системы (OpenTS). Синтаксически язык T++ максимально приближен к языку C++. В языке T++ поддерживается функциональный подход к написанию программ: все данные Т-функция («чистая» функция в языке Т++) может получать только через входные аргументы, а результаты своей работы возвращать только через выходные аргументы. Т-функция не должна иметь побочных эффектов. Таким образом, Т-функция является гранулой параллелизма: при вызове данной функции всю информацию она получает через свои аргументы, поэтому ее можно отдать на выполнение другому процессору. Описанный выше алгоритм решения задачи априорного определения границ изменения параметров возможных орбит реализован в Т-системе (язык программирования Т++). Рекомендуется следующая организация разработки программы на языке T++. 1. На этапе построения алгоритма разрабатывается его верхний уровень на базе парадигмы функционального программирования. 2. Этап разработки программного кода включает в себя решение вопроса о том, какие фрагменты алгоритма (какая часть программного кода) будут реализованы в виде Т-функций, а какая часть в виде привычного последовательного исполняемого кода в стандарте языка С++. 3. Этап реализации программы и ее первичной отладки на однопроцессорном компьютере. 4. Этап отладки на многопроцессорной установке заключается в отладке программы на одиночном SMP-компьютере и в дальнейшем запуске на кластере. Отметим, что при реализации программы для Т-системы программист обязан адекватно изложить алгоритм в функциональном стиле − описать программу в виде набора T-функций. Кроме этого, он должен стремиться выбрать оптимальный размер Т-функции (оптимально подобрать среднюю вычислительную сложность Т-функции). Так, слишком малая вычислительная сложность Т-функций может привести к большим накладным расходам (например, время, затраченное на передачу Т-функций и данных для них на другие узлы кластера, превысит время счета самой этой функции). В то же время слишком большая вычислительная сложность Т-функций может привести к малому количеству порождаемых в процессе счета гранул параллелизма и, как следствие, к неравномерной загрузке вычислительных узлов кластера. Рассмотрим фрагмент кода, отвечающий за параллельное исполнение программы: #define ND 100 #define NBOUNDS 64 #define NVEC 26 … struct result_bounds_s { double result_bounds[NBOUNDS]; }; struct vhod_vector_s { double vhod_vector[NVEC]; }; … tfun struct result_bounds_s track_bounds(unsigned int Max_iters, double eps_const, struct vhod_vector_s vhod_vector_e) { // код Т-функции … } tfun int main(int argc, char* argv[]) { … struct vhod_vector_s vhod_vector_e; … tval struct result_bounds_s result_bounds_t[ND]; for (unsigned int data = 0; data < ND; data++) { … result_bounds_t[ND] = track_bounds(Max_iters, eps_const, vhod_vector_e); … } … return 0; } … Видно, что при написании программы к стандартному набору С++ были добавлены лишь два ключевых слова языка Т++: tval и tfun. Атрибут tval можно указывать непосредственно перед описанием типа переменной, при этом переменная кратко называется Т-переменной и содержит неготовую величину. Неготовые величины производятся с помощью вызова Т-функций и в каждый момент времени либо не готовы (при этом их значение не определено, а попытка обращения к ним влечет за собой приостановку обращающейся функции), либо готовы, то есть уже посчитаны. Нельзя изменить собственно неготовую величину, но можно присвоить Т-переменной другую неготовую величину. Атрибут tfun указывается непосредственно перед описанием типа функции, а соответствующая функция кратко называется Т-функцией (в данном случае Т-функция – это функция track_bounds()). Т-функции являются гранулами параллелизма. При этом они могут одновременно выполняться на разных процессорах (узлах) в многопроцессорной системе. Отметим, что функция main() также должна быть объявлена как Т-функция. Описанный выше алгоритм решения задачи априорного определения границ изменения параметров возможных орбит реализован в Т-системе (язык программирования Т++). Результаты исследования эффективности параллельной версии программы для обработки 100 треков представлены в таблице 3. При расчете в последовательном режиме, исходя из требований целостности процесса работы комплекса программ ОТИ, наложено ограничение на среднее время обработки одного трека значением 0,7 с. Данное ограничение позволяет провести лишь три итерации и, как следствие, достигнуть относительной погрешности 2,5 %. Задача состояла в увеличении числа итераций (для достижения требуемой точности 0,3 %) с сохранением среднего времени обработки одного трека. Таблица 3 Время выполнения параллельной версии программы Table 3 Execution time of the parallel version of the program
Из таблицы видно, что для достижения выбранной точности среднее время обработки одного трека удается сделать приемлемым при расчете на 8 ядрах суперкомпьютера. Все эксперименты производились на тестовом кластере, расположенном в Институте программных систем имени А.К. Айламазяна РАН. На основании изложенного можно сделать следующие выводы. Переход к регулярному наблюдению и каталогизации малоразмерных ОКМ потребует совершенствования применяемых методов и алгоритмов получения и обработки информации. Одним из направлений решения этой проблемы является повышение эффективности работы оптических средств, которым в мониторинге малоразмерных ОКМ отводится значительная роль. В статье для ускорения обнаружения и определения орбит некаталогизированных ОКМ предложен вспомогательный алгоритм построения для каждого трека границ параметров возможных орбит. Подобный подход позволяет оптимизировать работу комплекса программ ОТИ в целом и, в частности, существенно ускорить работу по определению орбит новых КО непосредственно в процессе сеанса наблюдений. Динамическое распараллеливание, обеспечиваемое Т-системой, имеет ряд преимуществ не только для случая, когда вопросы организации параллельного счета решаются во время исполнения программы, но и для выравнивания нагрузки в гетерогенных и/или меняющихся со временем параллельных вычислительных системах, а также для задач, обладающих гранулами различной тяжести, как, например, для случая реализованного алгоритма априорного расчета границ параметров возможных орбит. Литература 1. Yurasov V.S., Vygon V.G., Shargorodsky V.D. Features of detection and orbit determination of uncatalogued space debris //Proceedings of The Seventh US-Russian Space Surveillance Workshop, 2007. URL: http://aero.tamu.edu/ sites/default/files/faculty/alfriend/R7%20S3.1%20Yurasov.pdf (дата обращения: 19.06.2015). 2. Alby F. et al. Status of CNES optical observations of space debris in geostationary orbit // Advances in Space Research, 2004, vol. 34, no. 5, pp. 1143–1149. 3. Earl M.A., Racey T.J. The Canadian Automatic Small Telescope for Orbital Research (CASTOR). A RAVEN System in Canada // 1999 AMOS Technical Conference, Aug., 1999, pp. 401–410. 4. Klinkrad H. Monitoring Space–Efforts Made by European Countries // International Colloquium on Europe and Space Debris, sponsored by the Academie National de l’Air et de l’Espace, Toulouse, France (27–28 November 2002). URL: http://www.fas.org/spp/military/program/track/klinkrad.pdf (дата обращения: 19.06.2015). 5. Flury W. et al. Searching for small debris in the geostationary ring // ESA bulletin, 2000, vol. 104, pp. 92–100. 6. Payne P.T. New Deep Space Optical Search Strategies. Proceedings of the Fifth US/Russian Space Surveillance Workshop. St. Petersburg, 2003. URL: http://aero.tamu.edu/ sites/default/files/faculty/alfriend/Russia6thWorkshop/r5%20S5.3%20Payne.pdf (дата обращения: 19.06.2015). 7. Schildknecht T. et al. An optical search for small-size debris in GEO and GTO. Proceedings of the 2003 AMOS Technical Conference, 2003, vol. 9, pp. 12. 8. Flohrer T., Schildknecht T., Musci R. Proposed strategies for optical observations in a future European Space Surveillance network. Advances in Space Research, 2008, vol. 41, no. 7, pp. 1010–1021. 9. Roscoe C.W.T., Schumacher Jr P.W., Wilkins M.P. Parallel Track Initiation for Optical Space Surveillance using Range and Range-Rate Bounds. Advances in the Astronautical Sciences, 2014, vol. 150, pp. 989–1008. 10. Абрамов С.М., Кузнецов А.А., Роганов В.А. Кроссплатформенная версия Т-системы с открытой архитектурой // Параллельные вычислительные технологии (ПаВТ'2007): тр. Междунар. науч. конф. Челябинск: Изд-во ЮУрГУ. 2007. Т. 1. C. 115–121. 11. Кузнецов А.А., Роганов В.А. Экспериментальная реализация отказоустойчивой версии системы OPENTS для платформы WINDOWS CCS // Суперкомпьютерные системы и их применение (SSA'2008): тр. 2-й Междунар. науч. конф. Минск: Изд-во ОИПИ НАН Беларуси, 2008. C. 65–70. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=4032 |
Версия для печати Выпуск в формате PDF (8.21Мб) Скачать обложку в формате PDF (1.09Мб) |
| Статья опубликована в выпуске журнала № 3 за 2015 год. [ на стр. 80-87 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Использование возможностей математической библиотеки Intel MKL в параллельных программах на языке Т++ для Т-системы с открытой архитектурой
- Реализация некоторых приложений проекта Mantevo на платформе OpenTS DMPI
- Программный комплекс оптимизации законов управления
- Формирование барьера безопасности на космическом аппарате при угрозе воздействия космического мусора методами нечеткой логики
- Программные средства вейвлет-фрактально-корреляционного метода обнаружения объектов космического мусора
Назад, к списку статей



 определяются границы изменения параметров возможных эллиптических орбит: дальности riÎ[rimin, rimax], наклонения IiÎ[Iimin, Iimax] и долготы восходящего узла WiÎ[Wimin, Wimax] в заданной области изменения эксцентриситета eiÎ[eimin, eimax]. Далее находятся все тройки треков
определяются границы изменения параметров возможных эллиптических орбит: дальности riÎ[rimin, rimax], наклонения IiÎ[Iimin, Iimax] и долготы восходящего узла WiÎ[Wimin, Wimax] в заданной области изменения эксцентриситета eiÎ[eimin, eimax]. Далее находятся все тройки треков 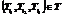 , такие, что
, такие, что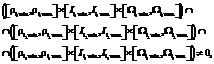
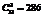 , а проведенный предварительный анализ треков позволил сократить число перебираемых троек до 13.
, а проведенный предварительный анализ треков позволил сократить число перебираемых троек до 13.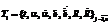 границ параметров орбиты, которой может принадлежать трек, при заданных интервалах изменения большой полуоси aiÎ[aimin, aimax] и эксцентриситета eiÎ[eimin, eimax]: границ возможного изменения дальности rÎ[rmin, rmax], наклонения IÎ[Imin, Imax], долготы восходящего узла WÎ[Wmin, Wmax]. Подобная задача рассматривалась в работе [9] и может быть разбита на последовательное решение следующих выделенных вспомогательных задач.
границ параметров орбиты, которой может принадлежать трек, при заданных интервалах изменения большой полуоси aiÎ[aimin, aimax] и эксцентриситета eiÎ[eimin, eimax]: границ возможного изменения дальности rÎ[rmin, rmax], наклонения IÎ[Imin, Imax], долготы восходящего узла WÎ[Wmin, Wmax]. Подобная задача рассматривалась в работе [9] и может быть разбита на последовательное решение следующих выделенных вспомогательных задач.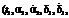
 ,
, 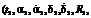
 t1
t1 a, r осуществляется построение соответствующих
a, r осуществляется построение соответствующих 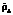 , e+.
, e+. получаются как решение уравнения относительно
получаются как решение уравнения относительно  (энергия − первый интеграл движения по кеплеровой орбите):
(энергия − первый интеграл движения по кеплеровой орбите): ,
, ;
;
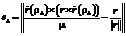 .
.
 , [emin, emax] найти границы изменения параметров a, r, I, W возможных орбит.
, [emin, emax] найти границы изменения параметров a, r, I, W возможных орбит. ,
, ,
,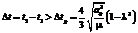 ,
,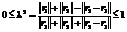 .
.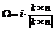 , где
, где  , i, k – единичные векторы экваториальной системы координат.
, i, k – единичные векторы экваториальной системы координат.
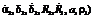 ,
,  . Получаются значения
. Получаются значения 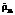 ,
,  и
и 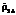 ,
, 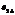 и их средние величины
и их средние величины  ,
,  . Вычисляются соответствующие им величины I+, W+ из соотношений
. Вычисляются соответствующие им величины I+, W+ из соотношений  ,
, 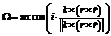 .
.


