В данной работе рассматриваются аспекты моделирования широкого класса систем, причем именно признаки событийности являются наиболее существенными для адекватного составления математических моделей. Признаки событийности и построенные на них методы моделирования [1–3] существенно отличают исследуемый подход от методов моделирования, общепринятых, например, в теории систем и теории автоматического управления, основными инструментами которых являются интегро-дифференциальные уравнения, методы теории вероятностей, математической статистики и случайных процессов. В теории систем и теории автоматического управления обычным описанием исследуемой системы является описание вход-выход, а изменение выхода относительно входа, то есть пространство состояний системы, задается передаточными функциями в матричном виде. Большинство систем, являющихся объектами моделирования, нелинейные, и в данном случае существенные усилия моделирования направлены на линеаризацию систем, выполняемую путем ре- шения систем дифференциальных уравнений в матричном виде. Результатами моделирования являются восстановленное фазовое пространство моделируемых систем и характеристики звеньев управления и регулирования.
Другим подходом является имитационное моделирование [4], использующее методы теорий систем и сетей массового обслуживания (СМО и СеМО соответственно) [5, 6], в которых рассматриваются различные модели входных, выходных потоков и правил обслуживания, построенных на базе соответствующих законов распределения случайных величин и процессов. В данном случае методами моделирования являются генераторы некоторых типов случайных процессов (имитирующих моменты времени поступления заявок на обслуживание), а результатами моделирования (часто усредненными) – времена пребывания заявки в очереди, системе, времена обслуживания, вероятности пребывания в очереди, вероятности обслуживания (за некоторый период) и другие вероятностные и статистические характеристики.
Заметим, что и в общей теории систем, и в теориях СМО и СеМО неявно предполагается использование процессного времени. Это означает, что в первом случае принимается, что процессы в системах протекают по возможности мгновенно (хотя в некоторых случаях допустима их инерционность), а во втором случае принимается, что процессы подчинены некоторому вероятностному закону. Однако во втором случае иногда рассматривают потоки general (общего) типа, в которых основным соотношением является рекуррентное уравнение Линдли [7], что по сути близко к рассматриваемому далее подходу с идейной стороны, но не со стороны реализации методов моделирования. В целом процессное время означает, что изменение состояний системы, а также ее модели можно отметить на некоторой временной шкале; если шкала является непрерывной, то естественным будет непрерывное моделирование состояний системы, иначе – дискретное, а также соответствующий им математический аппарат.
В основу дискретно-событийного моделирования, развиваемого появления известной системы GPSS [8] и сетей Петри [9, 10] положена другая концепция: состояния системы изменяются под воздействием некоторых событий, в общем случае безотносительно к их точной привязке к временной шкале. Существенными являются лишь факты возникновения этих событий и взаимодействие их между собой, то есть синхронизация (некоторое событие предшествует другому, некоторое событие вызывает возникновение другого либо других событий и так далее). Примером таких информационных систем являются сетевые компьютерные системы. Для сетевых компьютерных систем как многопользовательских многозадачных, многомашинных, многопроцессорных систем характерным является еще один аспект событийности – кон- куренция за сетевые распределенные вычислительные ресурсы с целью увеличения производительности, минимизации простоев и тому подобное. Оба этих аспекта (синхронизация и конкуренция) делают сетевые компьютерные системы существенно нелинейными, что усложняет их аналитическое и имитационное моделирование, а рассматриваемый далее в работе подход можно воспринимать как возможную линеаризацию таких систем.
Подходы и алгоритмы дискретно-событийного моделирования
Проведем грань между дискретно-событийным моделированием и другими методами моделирования более четко. Как уже упоминалось, большинство систем моделируется по принципу «вход–состояние–выход». Принимая общеизвестные обозначения векторов: u(t) – вход, x(t) – состояние, y(t) – выход, динамика моделируемой системы описывается уравнениями
x¢(t) = f (x(t), u(t), t), (1)
y(t) = g(x(t), u(t), t) (2)
с начальными условиями t > 0.
Уравнение (1) означает составление множества состояний моделируемой системы, а если принять, что множество таких состояний равно n, а множество входных сигналов равно m, то получается, что необходимо моделировать n уравнений состояний:
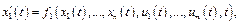
…,
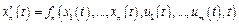
и k выходных уравнений системы:
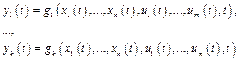
с начальными условиями x1(t0) = x1, …, xn(t0) = xn.
В зависимости от вида функций f и g, способа фиксации моментов времени t в (1, 2) осуществляется непрерывное (или дискретное) моделирование нелинейной (или линейной) динамической системы.
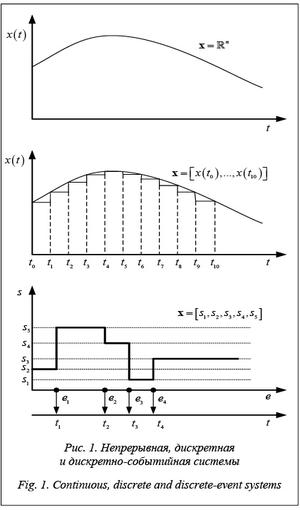 Еще раз следует заметить, что изменение состояний динамической системы в таких случаях моделирования всегда привязано ко времени, какими бы его измерениями мы ни пользовались, непрерывными или дискретными. В дискретно-событийном моделировании важен факт фиксации события (или группы событий), а в какое время, либо интервал времени, либо через какой промежуток времени эти события фиксируются, уже не столь важно. Получается, что «событие первично, а время вторично». В работе [11] имеются иллюстрации к вышесказанным положениям, которые приведены в доработанном виде на рисунке 1. В верхней части показано пространство состояний непрерывной системы, в средней – дискретной системы, а в нижней – дискретно-событийной системы. Ясно, что пространство состояний дискретно-событийной системы является дискретным и составляет события s1, …, s5, а переключение между этими состояниями происходит в соответствии с наступлением некоторых событий e1, …, e4. Естественно, при динамической смене состояний системы может происходить возврат к предыдущим состояниям, поэтому моделирование пространства состояний будет составлять при упорядочении по хронологии цепочек событий и совпадении момента времени и события (или группы событий) последовательность пар («время», «состояние»). В данном случае (рис. 1) это e0 = s2, {e1, e2, e3, e4} =
Еще раз следует заметить, что изменение состояний динамической системы в таких случаях моделирования всегда привязано ко времени, какими бы его измерениями мы ни пользовались, непрерывными или дискретными. В дискретно-событийном моделировании важен факт фиксации события (или группы событий), а в какое время, либо интервал времени, либо через какой промежуток времени эти события фиксируются, уже не столь важно. Получается, что «событие первично, а время вторично». В работе [11] имеются иллюстрации к вышесказанным положениям, которые приведены в доработанном виде на рисунке 1. В верхней части показано пространство состояний непрерывной системы, в средней – дискретной системы, а в нижней – дискретно-событийной системы. Ясно, что пространство состояний дискретно-событийной системы является дискретным и составляет события s1, …, s5, а переключение между этими состояниями происходит в соответствии с наступлением некоторых событий e1, …, e4. Естественно, при динамической смене состояний системы может происходить возврат к предыдущим состояниям, поэтому моделирование пространства состояний будет составлять при упорядочении по хронологии цепочек событий и совпадении момента времени и события (или группы событий) последовательность пар («время», «состояние»). В данном случае (рис. 1) это e0 = s2, {e1, e2, e3, e4} =
={(t1, s5), (t2, s4), (t3, s1), (t4, s3)}. (3)
Событийное функционирование обнаруживается у широкого класса современных систем. В области информационных систем и технологий событийными являются объектно-ориентированные программные системы, сетевые компьютерные, интерактивные, диалоговые системы и другие.
В формальном виде дискретно-событийная система – это некая разновидность временнόго автомата [11], который представляется в следующем виде.
Определение 1. Модель дискретно-событийной системы представляет собой кортеж
DS = (X, E, f, Г, x0), (4)
где X – конечное множество, пространство состояний системы; E – конечное множество событий; f – функция смены состояний, f: X ´ E ® X; Г – конечное множество активных (и исполняемых в текущий момент) событий; x0 – начальное состояние.
В связи с тем, что время как таковое не присутствует в модели (4), но при имитационном моделировании все же необходимо воспроизводить хронологию событий по мере упорядоченности их между собой, (4) дополняется модельными часами, связанными с множеством событий. Такие модельные часы представляют собой конечное множество
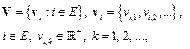 (5)
(5)
где vi,k – время жизни (продолжительность) события.
Для последовательности событий {e1, e2, …, ek, ek+1, …} можно «включить модельные часы» (5), получить V = {vi : i = 1, …, m} и генерировать события ek+1 = h(xk, v1, …, vm). Динамика состояний дискретно-событийной системы при этом определяется уравнением xk+1 = f (xk, v1, …, vm).
Таким образом, очень существенной задачей является формирование (генерация) списков событий, то есть пар вида (3), в зависимости от которой можно выделить событийно-ориентированное и процессно-ориентированное исполнение событий. Рассмотрим их более подробно.
Событийно-ориентированное моделирование в дискретно-событийной системе проиллюстрировано на рисунке 2.
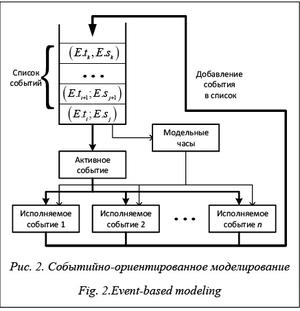 Список событий является динамической структурой, а модельные часы содержат время последнего исполняемого события. В алгоритмическом виде моделирование заключается в следующей последовательности действий.
Список событий является динамической структурой, а модельные часы содержат время последнего исполняемого события. В алгоритмическом виде моделирование заключается в следующей последовательности действий.
Алгоритм 1. Событийно-ориентированное моделирование.
1. Установить модельные часы в 0. Инициализировать начальный список событий, расположив их в хронологическом порядке следования. Элемент списка событий имеет структуру (E.ti; E.sj) и характеризуется временем и типом состояния (ti, sj).
2. Выбрать событие E из начала списка. Если список пуст, завершить моделирование.
3. Установить модельные часы в E.ti. Проверить длительность события и при превышении времени, отведенного на моделирование, завершить его.
4. В соответствии с типом события и состояния E.sj исполнить подпрограмму-обработчик события.
5. Обновить список событий, системные переменные и структуры, поместить новое событие в список событий.
6. Продолжить моделирование, перейдя к п. 2.
Элементы возможной программной реализации алгоритма 1 показаны в примере 1.
Пример 1. Основной событийно-ориентированный обработчик.
event_oriented()
{
sim_time = 0; // Начальное время = 0
list_init(); // Инициализация списка событий
done = FALSE; // Признак завершения моделирования
while(!done) // Основной обработчик событий
{
next_event(status,time); // Выбор события из списка
stime = time; // Фиксация времени
if (stime > max_sim_time) // Проверка превышения времени
{
done = TRUE; // Установка признака завершения
break; // Выход по завершении
}
exec_event(status); // Обработка события
}
}
Обработчик устанавливает начальное время, инициализирует список событий и в цикле, выбирая следующее событие, переустанавливает модельные часы, проверяя, чтобы не было превышения максимально допустимого времени моделирования, вызывает подпрограмму exec_event(status). При ее реализации имеет смысл запрограммировать хотя бы простейшее планирование списка событий в виде динамической очереди FIFO (First In First Out).
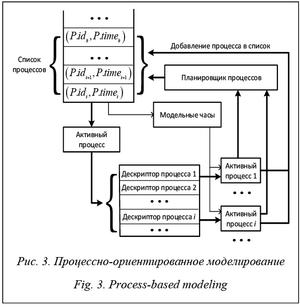 Во втором подходе, процессно-ориентированном исполнении событий, есть возможность исполнения группы событий при их логическом объединении в процессы, как показано на рисунке 3.
Во втором подходе, процессно-ориентированном исполнении событий, есть возможность исполнения группы событий при их логическом объединении в процессы, как показано на рисунке 3.
Основным отличием данного вида от предыдущего является не только возможность объединять процессы в группы, но и планировать переключение между процессами, разделяя при этом совместные ресурсы моделируемой системы. Общая схема такого моделирования представлена в виде алгоритма 2.
Алгоритм 2. Процессно-ориентированное моделирование.
1. Установить модельные часы в 0. Инициализировать начальный список событий, расположив их в хронологическом порядке следования. Элементы списков событий группируются в процессы, имеющие структуру (P.idi; P.timei), и характеризуются идентификатором и временем (id; time). Запустить основной цикл моделирования.
2. Создать активный процесс P из списка планируемых к исполнению событий. Если список пустой, завершить моделирование.
3. Проверить превышение максимального времени, отведенного на моделирование. Если есть превышение, моделирование завершить.
4. Присвоить процессу дескриптор исполнения и передать его планировщику процессов.
5. Выполнить планирование процессов: исполнение, ожидание, переключение, завершение.
6. В рамках процесса требуется исполнить обработчики событий, генерировать новые события.
7. Перейти к п. 2.
В примере 2 приведена схема возможной программной реализации.
Пример 2. Схема процессно-ориентированного обработчика
event_job(descriptor) // Планировщик процессов (пример)
{
while (TRUE)
{
wait(resource); // Ожидать свободные ресурсы
exec_event(status, time);// Исполнять обработчик события
switch(descriptor)); // Переключать на другой процесс
signal(release_event); // Завершить процесс
}
}
process_init() // Инициализация процесса
{
for (i=0;i
event_job(descriptor); // Планировать процесс
if (stime < max_sim_time)
{
next_event(status, time) // Выбор события из списка
stime = time; Фиксация времени
}
else break;
}
process_oriented()/*Основной процессно-ориентированный обработчик*/
{
stime = 0;
process_init();
simulate(stime);
}
Возможной простейшей стратегией планировщика могут являться FCFS (First Come First Served), «первый пришел – первый обслужен», а также реализация семафорного переключения контекста процессов.
Таким образом, научные исследования в области дискретно-событийного моделирования сейчас достаточно широко развиты в различных направ- лениях [12–15], а также являются значительным дополнением к методам имитационного моделирования систем. Существуют также программные реализации дискретно-событийных систем моделирования, например AnyLogic, SimPy, SimEvents и другие программные системы.
Дискретно-событийный подход к оценке надежности ПО
В целом дискретно-событийный подход опирается на упомянутые ранее идеи роста надежности ПО, однако в отличие от известных моделей будет использоваться покомпонентная технология моделирования событий возникновения ошибок на входе и выходе программного компонента. Процессы обнаружения и устранения ошибок моде- лируются случайными точечными процессами, а времена обнаружения ошибок сопоставляются с событиями, при возникновении которых требуется рассчитать вероятностные оценки надежности программных компонентов, которые в зависимости от реализуемых ими алгоритмов будут иметь разные формулы для расчета.
Процедуры моделирования в предлагаемом подходе можно разделить на две группы. Первая группа предназначена для генерации процессов, имитирующих появление ошибок в ПО. Сгенерированные модельные значения разделяются на несколько классов и составляют исходные данные для следующей группы процедур, которая предназначена для оценки системной надежности компонентного ПО. Модельные значения, разделенные на классы, сопоставляются с различными классами ошибок в событийной модели типа «вход–структура–выход». При этом анализируемый с точки зрения надежности программный компонент также относится к одному из классов в зависимости от используемых в нем программных конструкций. Каждому варианту программной конструкции соответствует отдельный вариант расчета оцениваемой надежности ПО.
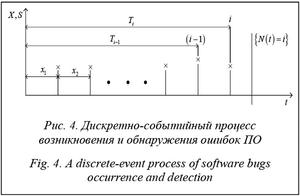
Рассмотрим подробнее модели первой группы. Определим следующие переменные: N(t) – кумулятивное (накопленное) число ошибок ПО, выявленных на стадиях разработки и тестирования до временного момента t; Ti – i-й интервал времени возникновения либо обнаружения ошибки (T0=0, i = 1, 2, …); Xi – интервал времени между (i–1)-й и i-й ошибками (X0 = 0, i = 1, 2, …).
На рисунке 4 показано возникновение события {N(t) = i}, которое означает, что было обнаружено i ошибок к моменту времени t.
Таким образом, имеем следующий принцип моделирования: 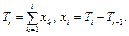
 Обозначим Si(x) уровень ошибок, то есть величину, пропорциональную числу необнаруженных (и, следовательно, неисправленных) ошибок для каждого из интервалов времени xi, i = 1, 2, …, общий подход к дискретно-событийному моделированию можно определить как
Обозначим Si(x) уровень ошибок, то есть величину, пропорциональную числу необнаруженных (и, следовательно, неисправленных) ошибок для каждого из интервалов времени xi, i = 1, 2, …, общий подход к дискретно-событийному моделированию можно определить как
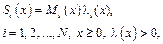 (6)
(6)
где Mi(x) – функция, задающая начальные условия модели; l(x) – функция интенсивности ошибок.
Естественно, в законе моделирования (6) функции Mi(x) и li(x) могут быть заданы различными зависимостями – от константы до выражения, имеющего сложную форму. Сама же функция надежности ПО (обозначим ее Rn (x)) исходя из (6) также может иметь разный вид, например:
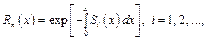
а числовая характеристика, определяющая среднее время между ошибками, может иметь вид
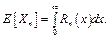
Последовательность процедур моделирования, составляющих первую группу методов моделирования, следующая.
1. Установление исходных положений моделирования.
1.1. Ошибки ПО возникают в случайные интервалы времени, отсчитываемые последовательно на одной временной оси; имеется некоторое число скрытых ошибок ПО, которые можно обнаружить на этапах разработки и тестирования.
1.2. Ошибка в ПО вызывает ошибочное состояние всей системы и требует ее исправления для восстановления функциональности системы.
1.3. Процесс исправления ошибки выполняется немедленно, новые ошибки при этом не вносятся.
2. Выбор математического аппарата моделирования.
Выбираем случайный считающий процесс N(t), t ³ 0, подсчитывающий кумулятивное число ошибок в ПО, детектированных ко времени t.
Условия и ограничения следующие: N(0) = 0.
2.1. {N(t), t ³ 0} – имеет независимые приращения.
2.2. 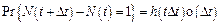 , где h(t) – функция мгновенной интенсивности детектирования ошибок.
, где h(t) – функция мгновенной интенсивности детектирования ошибок.
2.3. 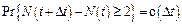 – в один момент времени обнаруживается не более одной ошибки.
– в один момент времени обнаруживается не более одной ошибки.
3. Генерация модельного процесса.
Генерируем неоднородный случайный пуассоновский процесс:
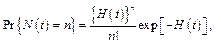 (7)
(7)
n = 0, 1, 2, …, где H(t) – ожидаемое кумулятивное число детектированных ошибок,
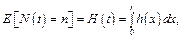
где h(x) – интенсивность обнаружения и исправления ошибок.
4. Переход к численному и алгоритмическому моделированию процессов.
В упрощенной форме выражение (7) моделируется дискретным неоднородным пуассоновским процессом со средним кумулятивным количеством детектированных ошибок Dn следующим образом:
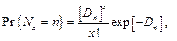 (8)
(8)
(x, n = 0, 1, 2, …).
В дальнейшем вместо выражения (8) могут использоваться другие различные дискретные аналоги выражения (7).
Рассмотрим один из таких аналогов, построенный на основе экспоненциальной модели роста. Пусть Hn обозначает кумулятивное число обнаруженных ошибок за некоторые n периодов эксплуатации ПО, его тестирования, отладки и тому подобное. Процесс роста надежности ПО описывается разностным уравнением
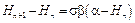 , (9)
, (9)
где s – некоторая константа; a – ожидаемое число ошибок на бесконечно длинном интервале времени; b – интенсивность обнаружения ошибок.
Для численной оценки параметров a и b из (9) составим уравнение регрессии: Yn = A + BHn, где Yn = Hn+1 – Hn, A = dab, B = –db.
Имея статистические данные по числу обнаруженных ошибок (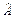 и
и 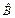 ), получаем оценки требуемых параметров из (9):
), получаем оценки требуемых параметров из (9): 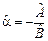 и
и 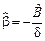 .
.
Перейдем к процедурам второй группы, где разработана компонентная модель оценки надежности ПО, учитывающая несколько классов ошибок.
5. Формальное представление компонентной модели оценки надежности ПО.
Определение 2. Компонентную модель оценки надежности ПО, учитывающую структуру программных конструкций и классы ошибок, определим следующим образом. Имеются три класса ошибок:
1) 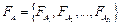 – некритические, не воздействующие на выход своего и вход другого блока;
– некритические, не воздействующие на выход своего и вход другого блока;
2) 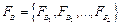 – переходящие, воздействующие на выход своего и вход другого блока;
– переходящие, воздействующие на выход своего и вход другого блока;
3) 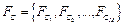 – критические, воздействующие на выход своего и не воздействующие на вход другого блока.
– критические, воздействующие на выход своего и не воздействующие на вход другого блока.
Оценкой надежности компонента с различной программной конструкцией будем считать вероятность возникновения события, связанного с проявлением ошибки любого вышеуказанного класса, рассматривая программный компонент как систему «вход–структура–выход» Pr(I, O), I Î FB, O Î (FBÈ FC), причем 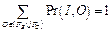 ,"I Î FB.
,"I Î FB.
6. Варианты расчетов возникновения события, сигнализирующего о появлении ошибки ПО.
В связи с заявленным типом модели «вход–структура–выход» рассмотрим варианты расчета вероятности возникновения события, вызванного ошибкой в зависимости от структуры програм- много компонента.
6.1. Последовательная структура.
На рисунке 5 показана последовательная структура исполнения алгоритмов A1, A2, …, An программного компонента.

Вычислительная схема 1.
1. Генерация вероятностей 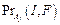 ,
, 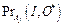 ,
, 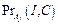 , I Î FB, F Î FA, O* Î FB, C Î FC, j = 1, …, n.
, I Î FB, F Î FA, O* Î FB, C Î FC, j = 1, …, n.
2. Для имитации возникновения некритической ошибки на выходе An: 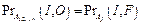 , где F Î FA.
, где F Î FA.
3. Для имитации возникновения переходящей ошибки на выходе An: 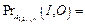
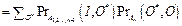 , где O* Î FB.
, где O* Î FB.
4. Для имитации возникновения критической ошибки на выходе An: 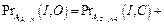
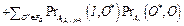 , где O*ÎFB, CÎFC.
, где O*ÎFB, CÎFC.
6.2. Разветвляющаяся структура.
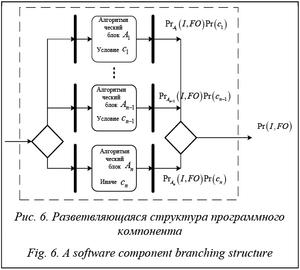 Если программный компонент имеет структуру разветвления с cn ветвями, из которых первые n – 1 являются ветвями «если–то», а n-я ветвь общим «иначе», то расчет будет производиться по вычислительной схеме 2 (рис. 6).
Если программный компонент имеет структуру разветвления с cn ветвями, из которых первые n – 1 являются ветвями «если–то», а n-я ветвь общим «иначе», то расчет будет производиться по вычислительной схеме 2 (рис. 6).
Вычислительная схема 2.
1. Генерация вероятностей 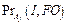 , I Î FB, FO Î (FB È FC), j = 1, …, n, Pr(ci), i = 1, …, n – 1.
, I Î FB, FO Î (FB È FC), j = 1, …, n, Pr(ci), i = 1, …, n – 1.
2. Для имитации возникновения ошибки рассчитывается 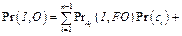
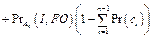 .
.
6.3. Циклическая структура.
Если программный компонент имеет циклическую структуру, ее можно трансформировать в n-кратное повторение последовательной структуры исполнения алгоритма 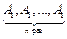 програм- много компонента. Таким образом, для циклической структуры оказывается подходящей вычислительная схема из п. 6.1.
програм- много компонента. Таким образом, для циклической структуры оказывается подходящей вычислительная схема из п. 6.1.
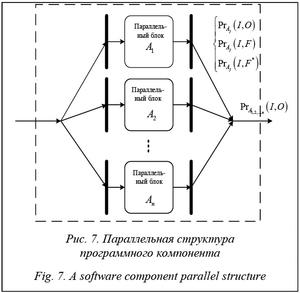
6.4. Параллельная структура.
Если программный компонент предусматривает параллельное исполнение n алгоритмов A1, A2, …, An, то моделируется возникновение событий, связанных с классами некритичных и критичных ошибок. Структура исполнения алгоритмов в этом случае показана на рисунке 7.
Вычислительная схема 3.
1. Генерация вероятностей 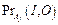 ,
, 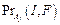 ,
, 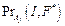 , I Î FB, F* Î FA, F Î (FA È FC) j = 1, …, n.
, I Î FB, F* Î FA, F Î (FA È FC) j = 1, …, n.
2. Если n – 1 параллельных ветвей имеют корректный выход, а n-я ветвь имеет некритическую ошибку, то рассчитывается 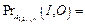
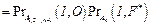 .
.
3. Если n – 1 параллельных ветвей имеют некритическую ошибку, а n-я ветвь имеет критическую ошибку либо наоборот, то рассчитывается 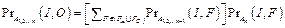 .
.
На основании изложенного сделаем следующие выводы. В статье предложен дискретно-событийный подход к оценке надежности ПО, использующий покомпонентную технологию моделирования событий возникновения ошибок на входе и выходе программного компонента. Процессы обнару- жения и устранения ошибок моделируются слу- чайными точечными процессами, а времена обнаружения ошибок сопоставляются с событиями, при возникновении которых требуется рассчитать вероятностные оценки надежности программных компонентов, которые в зависимости от реализуемых ими алгоритмических структур имеют разные формулы для расчета.
Литература
1. Banks J. Discrete-event system simulation. Pearson Prentice Hall, 2005, 608 p.
2. Tyszer J. Object-oriented computer simulation of discrete-event systems. Springer US, 1999, 258 p.
3. Wainer G.A. Discrete event modeling and simulation: a practitioner’s approach. CRC Press, 2009, 486 p.
4. Лоу А.М., Кельтон В.Д. Имитационное моделирование. Классика CS. 3-е изд. СПб: Питер; Киев: BHV, 2004. 847 с.
5. Рыжиков Ю.И. Имитационное моделирование. Теория и технологии. М.: Альтекс-А, 2004. 384 с.
6. Финаев В.И. Алгоритмизация и имитационное моделирование с применением аппарата систем массового обслуживания: учеб. пособие. Таганрог: Изд-во ТРТУ, 2003. 155 с.
7. Таха Х.А. Введение в исследование операций. 7-е изд.; [пер. с англ.]. М.: Вильямс, 2005. 912 с.
8. Бражник А.Н. Имитационное моделирование: возможности GPSS WORLD. СПб: Реноме, 2006. 439 с.
9. Котов В.Е. Сети Петри. М.: Наука, 1984. 160 с.
10. Hruz B., Zhou M.C. Modeling and Control of Discrete-event Dynamic Systems: with Petri Nets and Other Tools. Springer London, 2007, 341 p.
11. Cassandras C.G., Lafortune S. Introduction to discrete event systems. 2nd Edition. Springer, 2008, 782 p.
12. Baccelli F., Cohen G., Olsder G.J., Quadrat J.-P. Synchronization and linearity: an algebra for discrete event systems. Chichester: Wiley, 1992, 514 p.
13. Gondran M., Minoux M. Graphs, Dioids and Semirings. New Models and Algorithms. Springer Science+Business Media, LLC. 2008, 384 p.
14. Heidergott B., Jan Olsder G., van der Woude J. Max Plus at work. Modeling and analysis of synchronized systems: A course on Max-Plus Algebra and Its Applications. Princeton Univ. Press, Princeton. 2006, 232 p.
15. Wainer G.A. Discrete Event Modeling and Simulation: A practitioner’s approach. CRC Press, 2009, 486 p.



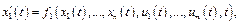
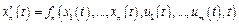
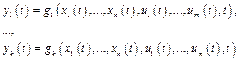

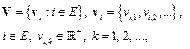 (5)
(5)

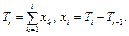

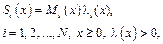 (6)
(6)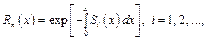
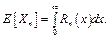
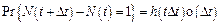 , где h(t) – функция мгновенной интенсивности детектирования ошибок.
, где h(t) – функция мгновенной интенсивности детектирования ошибок.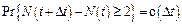 – в один момент времени обнаруживается не более одной ошибки.
– в один момент времени обнаруживается не более одной ошибки.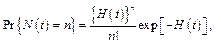 (7)
(7)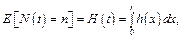
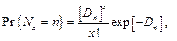 (8)
(8)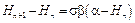 , (9)
, (9)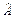 и
и 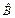 ), получаем оценки требуемых параметров из (9):
), получаем оценки требуемых параметров из (9): 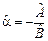 и
и 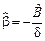 .
.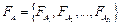 – некритические, не воздействующие на выход своего и вход другого блока;
– некритические, не воздействующие на выход своего и вход другого блока;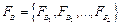 – переходящие, воздействующие на выход своего и вход другого блока;
– переходящие, воздействующие на выход своего и вход другого блока;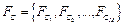 – критические, воздействующие на выход своего и не воздействующие на вход другого блока.
– критические, воздействующие на выход своего и не воздействующие на вход другого блока.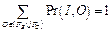 ,"I Î FB.
,"I Î FB.
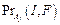 ,
, 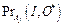 ,
, 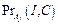 , I Î FB, F Î FA, O* Î FB, C Î FC, j = 1, …, n.
, I Î FB, F Î FA, O* Î FB, C Î FC, j = 1, …, n.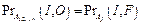 , где F Î FA.
, где F Î FA.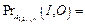
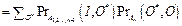 , где O* Î FB.
, где O* Î FB.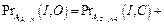
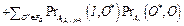 , где O*ÎFB, CÎFC.
, где O*ÎFB, CÎFC.
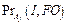 , I Î FB, FO Î (FB È FC), j = 1, …, n, Pr(ci), i = 1, …, n – 1.
, I Î FB, FO Î (FB È FC), j = 1, …, n, Pr(ci), i = 1, …, n – 1.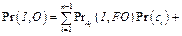
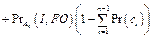 .
.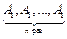 програм- много компонента. Таким образом, для циклической структуры оказывается подходящей вычислительная схема из п. 6.1.
програм- много компонента. Таким образом, для циклической структуры оказывается подходящей вычислительная схема из п. 6.1.
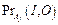 ,
, 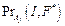 , I Î FB, F* Î FA, F Î (FA È FC) j = 1, …, n.
, I Î FB, F* Î FA, F Î (FA È FC) j = 1, …, n.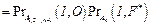 .
.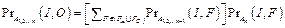 .
.