Прежде чем выполнять верификацию для конкретной системы, необходимо сформулировать те ее свойства, наличие или отсутствие которых требуется доказать. Привычная разговорная и письменная речь зачастую не позволяет сделать это однозначно, поэтому были разработаны специальные механизмы для решения данной проблемы [1, 2], в частности, метод, основанный на использовании различных моделей временной логики: логики линейного времени (LTL), ветвящегося времени (CTL), а также обобщающей их логики CTL* [3–5]. Данные логики лишены недостатков с точки зрения однозначности формулируемых на их базе свойств. Однако, как показывает практика, их мощность позволяет формулировать лишь относительно небольшое количество однотипных условий, а этого, в свою очередь, может быть недостаточно для проверки тех или иных свойств модели конкретной системы.

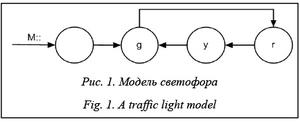Рассмотрим, например, модель работы светофора, представленную на рисунке 1 структурой Крипке [6].

Предикаты модели принимают следующие значения: g – включен зеленый сигнал светофора, r – красный, y – желтый. Как видим, светофор из своего некоторого первоначального состояния переходит в режим, в котором наступает строгое чередование зеленого, красного и желтого сигналов. Предположим, что стоит задача верификации работы этого режима с доказательством строгого чередования сигналов. Представить это можно в виде развертки, изображенной на рисунке 2.

И здесь встает проблема, решение которой невозможно в рамках любой из имеющихся логик: определить свойство строгого чередования трех предикатов на бесконечном интервале в случае необходимости его проверки и сформулировать чередование любого произвольного конечного числа предикатов. В общем виде в LTL свойство чередования для предложенного светофора можно определить с помощью оператора X (на следующем шаге) как φ = Xg ∧ XXr ∧ XXXy ∧ XXXXg ∧… Несмотря на то, что запись G(g ∧ Xr ∧ XXy) кажется интуитивно правильной для данного примера, можно показать, что в действительности она описывает последовательность совершенно иного ха- рактера. А именно, используя правило G(p ∧ q) = = G(p) ∧ G(q), можно представить данную запись в виде G(g) ∧ G(Xr) ∧ G(XXy). Применяя правило рекурсивного определения оператора G вида Gp = = p ∧ X(p) ∧ XX(p) ∧ XXX(p)… для каждого из конъюнктов, получим

Gg = g ∧ X(g) ∧ XX(g) ∧ XXX(g)…

G(Xr) = Xr ∧ X(Xr) ∧ XX(Xr) ∧ XXX(Xr)…

G(XXy) = XXy ∧ X(XXy) ∧ XX(XXy) ∧ XXX(XXy)…

Объединив их, получим последовательность вида φ = g ∧ X(g ∧ r) ∧ XX(g ∧ r ∧ y) ∧ XXX(g ∧ r ∧ y)…

Очевидно, что данная последовательность не совпадает с описанной ранее последовательностью. Этот пример иллюстрирует неэффективность оператора G в задачах определения строгого чередования предикатов на бесконечной последовательности состояний.

Таким образом, встает проблема разработки некоторого механизма формулировки свойств системы, который позволял бы расширить базовое множество типовых выражений и был бы достаточно удобным для выполнения проверки на моделях.

Эквациональная характеристика операторов LTL (RLTL)

Рассмотрим рекурсивные представления основных базовых операторов логики LTL (табл. 1).

 

Символ «∘» обозначает оператор продолжения (конкатенация выражений), что позволяет использовать оператор X в неявном виде, а также упростить его восприятие, в частности, запись φ1 ∘ φ2 будет пониматься как «φ2 следует за φ1». Под символом «∆», далее именуемым предикатом неопределенности, будем понимать неопределенное множество предикатов для конкретного состояния вычислительной последовательности относительно тех предикатов, которые принимают в нем истинностные значения.

В таблице 1 представлены все операторы, используемые в LTL. Поскольку все основные операторы LTL могут быть приведены к своим рекурсивным представлениям, авторы полагают, что приведение их к некоторому унифицированному виду, который в последующем именуется эквациональной характеристикой, позволит существенно расширить описательную способность логики LTL и упростит процесс верификации ее формул.

Сочетания операторов LTL также могут быть выведены с помощью аксиом в рамках эквациональной характеристики. В таблице 2 приведены некоторые сочетания операторов LTL.

Примеры описания свойств в RLTL-нотации

Рассмотрим некоторые типы свойств, описать которые можно, лишь используя предлагаемый механизм эквациональной характеристики для логики LTL. Одним из таких типов будет тип строго чередующихся последовательностей предикатов на бесконечной вычислительной последовательности состояний. В общем виде данный тип представлен на рисунке 3.

Общий вид данного типа задается системой рекурсивных уравнений Φ:

Fr1 = p1 ∘ Fr2,

Fr2 = p2 ∘ Fr3,

… 

Fr(n) = pn ∘ Fr1.

Пример данного типа уже был рассмотрен при описании модели работы светофора. Сформулируем заданное для нее в общем виде условие φ = Xg ∧ XXr ∧ XXXy ∧ XXXXg ∧… с помощью эквациональной характеристики:

Fr1 = ∅ ∘ Fr2;

Fr2 = g ∘ Fr3;

Fr3 = r ∘ Fr4;

Fr4 = y ∘ Fr2.

Под символом «∅» в дальнейшем будем понимать пустое множество предикатов, означающее, что ни один из предикатов множества AP [6] не принимает значение «истина». Таким образом, сформулированное условие представляет собой систему из четырех рекурсивных уравнений, строго задающих необходимую последовательность предикатов (сигналов светофора).

Еще одним типом свойств, которые нельзя выразить стандартными формулами LTL, является вхождение (появление) вложенных последовательностей предикатов на бесконечной вычислительной последовательности состояний. В общем виде данный тип изображен на рисунке 4.

Условно данный тип может быть описан как тип постепенного переключения режимов работы системы, где переход в каждый последующий режим возможен лишь в случае корректного выполнения предыдущего, причем последовательности включения и выключения этих режимов строго взаимообратные.

Представим данный тип в виде системы рекурсивных уравнений Φ:

Fr1 = ∅ ∘ Fr1 ∨ a ∘ Fr2;

Fr2 = a ∘ Fr2 ∨ (a ∧ b) ∘ Fr3;

…

Fr(k) = (a ∧ b) ∘ Fr(k) ∨ a ∘ Fr(k+1);

Fr(k+1) = a ∘ Fr(k+1) ∨ ∅ ∘ Fr1.

В качестве примера можно рассмотреть модель работы подсистемы космического спутника, отвечающую за работу передатчика и приемника радиосигнала (рис. 5).

Таким образом, развертка данной модели будет выглядеть так, как показано на рисунке 6.

Система рекурсивных уравнений, характеризующая данную последовательность, будет состоять из четырех уравнений:

Fr1 = ∅ ∘ Fr1 ∨ p ∘ Fr2;

Fr2 = p ∘ Fr2 ∨ (p ∧ t) ∘ Fr3;

Fr3 = (p ∧ t) ∘ Fr3 ∨ p ∘ Fr4;

Fr4 = p ∘ Fr4 ∨ ∅ ∘ Fr1.

Верификация RLTL

Покажем, что, задавая некоторое свойство, представленное системой рекурсивных уравнений, легко выполнить его верификацию на заданной модели. В качестве примера возьмем рассмотренную выше модель светофора, представленную на рисунке 1, а в качестве проверяемого условия – систему рекурсивных уравнений Φ, означающую то, что «со второго состояния светофора начинается строгое чередование зеленого, красного и желтого сигналов»:

Φ = Fr1 = ∅ ∘ Fr2;

Fr2 = g ∘ Fr3;

Fr3 = r ∘ Fr4;

Fr4 = y ∘ Fr2.

Для выполнения верификации формул RLTL будет использована та же самая методика верификации, что и для формул LTL, описанная в [6].

На первом этапе сформулируем отрицание проверяемого условия, используя аксиомы, приведенные выше:

˥Φ = ˥Fr1 = ˥∅ ∨ ∆ ∘ ˥Fr2;

˥Fr2 = ˥g ∨ ∆ ∘ ˥Fr3;

˥Fr3 = ˥r ∨ ∆ ∘ ˥Fr5;

˥Fr4 = ˥y ∨ ∆ ∘ ˥Fr2.

На втором этапе для полученной системы рекурсивных уравнений построим контрольный автомат. Для упрощения процесса построения контрольного автомата применим аксиому A15 к полу- ченной системе рекурсивных уравнений и получим следующую систему рекурсивных уравнений:

˥Φ = Fr1 = ˥∅ ∘ Fr5 ∨ ∆ ∘ Fr2;

Fr2 = ˥g ∘ Fr5 ∨ ∆ ∘ Fr3;

Fr3 = ˥r ∘ Fr5 ∨ ∆ ∘ Fr5;

Fr4 = ˥y ∘ Fr5 ∨ ∆ ∘ Fr2;

Fr5 = ∆ ∘ Fr5.

На третьем этапе необходимо представить ˥Φ в виде автомата Бюхи B˥Φ. Для этого построим такой автомат, в котором состояниям будут сопоставлены переменные Fi нашей рекурсивной системы уравнений, а переходам – предикаты. Как видно из рисунка 7, сделать это достаточно просто. Допускающими состояниями являются те, в которые существует хотя бы один переход по предикату, отличному от предиката неопределенности ∆.

Теперь построим композицию автомата B˥Φ и автомата Bm нашей модели светофора (рис. 8) согласно методу, описанному в [6]. Результатом композиции перехода, помеченного предикатом неопределенности ∆, с переходом, помеченным некоторым предикатом φ, является переход, помеченный φ, так как неопределенность устраняется. Результат композиции представлен на рисунке 9.

Жирными стрелками показаны переходы, которые достижимы из начального состояния (s1, 1). Очевидно, что из начального состояния невозможно попасть ни в одно из допускающих состояний, что означает невыполнимость ˥Φ, а следовательно, выполнимость Φ. Таким образом, свойство «со второго состояния светофора начинается строгое чередование зеленого, красного и желтого сигналов» действительно выполняется.

В заключение отметим, что в статье была рассмотрена проблема формулирования сложных верифицируемых свойств. Как показала практика, LTL и CTL не позволяют формулировать большой спектр условий, среди которых могут оказаться именно те, что необходимы для верификации конкретной модели. Предложенный в работе механизм эквациональной характеристики для логики LTL позволяет существенно расширить возможности ее описательных свойств. На основе данного механизма были рассмотрены два конкретных примера, относящихся к конкретным типам вычислительных последовательностей, представление которых невозможно в рамках стандартных формул LTL. Для первого примера продемонстрирован алгоритм верификации, показавший, что процесс построения контрольного автомата на базе системы рекурсивных уравнений является гораздо более удобным, интуитивно понятным и наглядным.

Авторы полагают, что использование данного представления формул временной логики позволит существенно увеличить гибкость и практичность верификации, поскольку предлагаемый метод может быть с легкостью внедрен в уже существую- щие технологии верификации на базе метода Model Checking или проверки на моделях.

Литература

1.    Кораблин Ю.П. Семантика языков распределенного программирования: учеб. пособие. М.: Изд-во МЭИ, 1996. 102 с.

2.     Hopcroft J.E., Motwani R., Ullman J.D. Introduction to Automata Theory, Languages, and Computation, 3/E – Pearson/Addison Wesley, 2007, 535 p.

3.     Велдер С.А., Лукин М.А., Шалуто А.А., Яминов Б.Р. Верификация автоматных программ. СПб: Наука, 2011. 244 с.

4.     Kröger F., Merz S. Temporal Logic and State Systems. Springer (March 27, 2008), 436 p.

5.     Manna Z., Pnueli A. The Temporal Logic of Reactive and Concurrent Systems: Specification. 1992, 427 p.

6.     Карпов Ю.Г. Model Checking. Верификация параллельных и распределенных программных систем. СПб: БХВ-Петербург, 2010. 552 с.

7.     Кораблин Ю.П., Куликова Н.Л. Логические методы доказательства и тестирования программ // Информационные средства и технологии: тез. докл. Междунар. конф. М.: Изд-во МФИ, 1996. 9 с.

8.     Кораблин Ю.П. Семантика языков программирования. М.: Изд-во МЭИ, 1992. 100 с.

9.     Кораблин Ю.П., Косакян М.Л. Анализ моделей программ на языке асинхронных функциональных схем средствами темпоральной логики линейного времени // Программные продукты и системы. 2014. № 2 (106). С. 5–10.

10.  Алагич С., Арбиб М. Проектирование корректных структурированных программ. М.: Радио и связь, 1979. 292 с.

11.  Hoare C.A.R. An axiomatic basis for computer programming. Northern Irelan: Queen's Univ. of Belfast, 1969, pp. 576–580.

12.  Ábrahám E., Havelund K. (Eds). Tools and Algorithms for the Construction and Analysis of Systems. Springer (March 24, 2014), 652 p.

13.  Bérard B., Bidoit M., Finkel A., Laroussinie F., Petit A., Petrucci L., Schnoebelen P. Systems and Software Verification. Model Checking Techniques and Tools. Springer, 2001, 190 p.