Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Оптимизационный алгоритм поиска вписанного многогранника максимального объема
Аннотация:Рассматривается задача нахождения многогранников заданной формы внутри других многогранников. Данная задача является частным случаем третьей части 18-й проблемы Гильберта. Она имеет практическое применение в компьютерном моделировании трехмерных объектов, автономном перемещении роботов, ювелирной промышленности. В статье предлагаются несколько альтернативных методов поиска вписанных многогранников, основанных на сведении данной задачи к задаче нелинейного программирования и решения ее с помощью готовых программных вычислительных ресурсов. Основная идея в том, что задача легко описывается в терминах нелинейного программирования. Целевой функцией является объем искомого многогранника. Ограничения включают в себя сохранение комбинаторной структуры, содержание многогранника внутри другого, выпуклость и дополнительные ограничения, необходимые для практических целей. В статье описаны два разных способа задания задачи нелинейного программирования и бесплатные программные ресурсы, которые могут быть использованы для решения этой задачи. Чтобы упростить работу с решателями задач нелинейного программирования, в качестве функций ограничений можно использовать только многочлены третьего порядка. Предложенные аппроксимации для основных типов ограничений позволяют сводить все необходимые ограничения к многочленам третьего порядка. Кроме того, в статье рассматривается система распределенного тестирования и эффективность алгоритма. Система тестирования написана на языке Python и используется для проверки и развития алгоритма. Она позволяет агрегировать данные по множеству запусков алгоритма в удобном для пользователя формате и сравнивать результаты разных версий алгоритма.
Abstract:The article discusses the problem of finding the polyhedrons with given shape inside other polyhedrons. This problem is a particular case of the third part of the 18th Hilbert problem. It can be applied in computer simulation of three-dimensional objects, the autonomous robots moving and the jewelry industry. The article offers several alternative methods of finding inscribed polyhedrons based on the reduction of the problem to a nonlinear programming problem and solving it using ready-made software resources. The basic idea is that the problem is easily described in terms of non-linear programming. Internal polyhedron volume is an objective function. Restrictions include saving a combinatorial structure, a polyhedron being inside another one, convexity and additional constraints that are necessary for practical purposes. This article describes two different ways to specify a nonlinear programming problem. In addition, it describes free software resources to solve this problem. To make work with non-linear programming solvers easier, only the third order polynomials can be used as the functions. The proposed possible approximations for the main types of restrictions allow to convert all the necessary restrictions to the third-order polynomials. Finally, the article describes a distributed testing system and the algorithm effectiveness. The testing system was developed in Python and is used to test and develop the algorithm. It allows aggregating data across multiple runs of the algorithm in a user-friendly format and comparing results of different versions of the algorithm.
| Авторы: Кокорев Д.С. (korvin-d@yandex.ru) - Институт проблем передачи информации им. А.А. Харкевича РАН (аспирант), Москва, Россия | |
| Ключевые слова: солвер, задача нелинейного программирования, вписанный многогранник, комбинаторная структура, выпуклые многогранники |
|
| Keywords: solver, nonlinear programming problems, inscribed polyhedron, combinatorial structure, convex polyhedrons |
|
| Количество просмотров: 4393 |
Версия для печати Выпуск в формате PDF (8.31Мб) Скачать обложку в формате PDF (1.24Мб) |
Одной из классических математических проблем является третья часть 18-й проблемы Гильберта. В своей общей постановке она посвящается упаковке одних тел другими. В случае упаковки правильными объектами, например сферами, существуют доказанные результаты, в частности, сильная проблема тринадцати сфер [1], проблема двадцати пяти сфер [2] и гипотеза Кеплера [3]. Для случая двухмерных многогранников и простых трехмерных объектов есть ряд решенных задач [4]. В случае упаковки многомерных многогранников в другие многогранники задача оказывается очень сложной, и пока не существует теоретических подходов к ней в общем виде. Частным случаем этой проблемы является задача нахождения в выпуклом многограннике произвольной формы объекта заданной формы с наибольшим объемом. Она имеет широкую область применения: компьютерное моделирование трехмерных объектов, программные тренажеры, компьютерные игры, приложения, решающие задачи упаковки и раскроя, программы, отвечающие за передвижение роботов, ювелирная промышленность, обработка дорогостоящих материалов. Описанный в статье алгоритм используется в коммерческих целях для нахождения оптимального плана бриллианта на разных стадиях огранки драгоценного камня. Первоначальным этапом алгоритма решения этой задачи является нахождение стартовой точки – начального приблизительного расположения объекта. В качестве стартовой точки могут быть взяты данные работы других неточных алгорит- мов. Один из примеров таких алгоритмов – гомотетичное раздувание под разными углами и с центром масс в разных точках искомого объекта до пересечения с внешним многогранником и нахождение, таким образом, стартовой точки с максимальным объемом, но в строго зафиксированной форме. Далее необходимо, шевеля вершины на незначительные расстояния, найти положение с максимальным объемом, удовлетворяющее некоторым требованиям на форму. Для реализации алгоритма были использованы сторонние программные ресурсы, организованные с помощью RESTful-веб-сервисов [5]. Такой подход позволяет не тратить время на разработку сложных математических алгоритмов, а использовать уже готовые решения и тем самым сконцентрироваться на поставленной задаче [6]. Более ранние исследования на тему вписывания многогранников описаны в [7]. Определение 1. Вписыванием одного многогранника в другой будем называть нахождение многогранника, комбинаторно эквивалентного первому, максимального объема и содержащегося во втором. Определение 2. Будем говорить, что два многогранника обладают одинаковой комбинаторной структурой тогда и только тогда, когда изоморфны их граничные комплексы [8]. Такие многогранники называются комбинаторно эквивалентными. Определение 2.1. Комплексом называется конечная совокупность K многогранников в Ed, удовлетворяющая следующим условиям: наряду с каждым многогранником М из семейства K в K входит также и любая грань многогранника М; пересечение любых двух многогранников из K является гранью каждого из них. Определение 2.2. Пусть М – d-многогранник (размерности d ) в Еd и целое число k удовлетворяет условию 0 < k < d. Множество всех граней многогранника М размерности, не превышающей k, является комплексом, который назван k-скелетом многогранника М. Определение 2.3. (d–1)-скелет многогранника М будем обозначать символом F(М) и называть граничным комплексом многогранника. Определение 2.4. Два комплекса, K и K', называются изоморфными комплексами, если между ними существует взаимно однозначное отображение φ, сохраняющее операцию включения: F1 ⊂ F2 ó φ (F1)⊂ φ (F2). Определение 3. Задачей нелинейного программирования (НП-задачей) называется оптимизационная задача следующего вида: f(x)→min при ограничениях gL≤ g(x)≤ gU, xL≤ x≤ xU, где xÎ xL f : g: gL f(x) и g(x) могут быть линейными или нелинейными, выпуклыми или невыпуклыми. Определение 4. AMPL (A Modeling Language for Mathematical Programming) – язык программирования высокого уровня для описания и решения сложных задач оптимизации и теории расписаний [9]. Главным преимуществом AMPL является подобие его синтаксиса математической записи задач оптимизации, что позволяет дать очень краткое и легко читаемое определение задач математического программирования. Для решения задач, написанных на AMPL, используются вычислительные солверы. Определение 5. Нелинейный солвер – программа для решения задач нелинейного программирования, использующая один из таких алгоритмов, как метод градиентного спуска, метод внутренней точки или квазиньютоновские методы. Определение 6. Выпуклой оболочкой множества X называется наименьшее выпуклое множество, содержащее X. Определение 7. Смешанным произведением (
Ориентированный объем симплекса в трехмерном евклидовом пространстве можно определить по формуле Постановка задачи Даны два выпуклых многогранника – внешний и внутренний. Внутренний многогранник является начальным приблизительным решением задачи и содержится внутри внешнего. Шевеля вершины, требуется максимально увеличить внутренний многогранник так, чтобы он остался вписанным и сохранил свою комбинаторную структуру. Помимо комбинаторной структуры, могут быть добавлены соотношения каких-либо размеров, фиксирующих форму многогранника, необходимые для прикладного использования алгоритма. Первый метод Поставленную геометрическую задачу необходимо записать в терминах задачи нелинейного программирования. В качестве целевой функции f(x) в нашем случае берется объем внутреннего многогранника. Он вычисляется через координаты вершин с помощью разбиения граней на треугольники и представление объема в виде суммы объемов симплексов. Если в прикладном применении метода ценность искомого объекта зависит не только от объема, то эти характеристики также можно внести в целевую функцию. Переменными в нашей задаче будут параметры, отвечающие за расположение вершин в пространстве, xijÎ(–¥, +¥), где j – номер точки, i – ось координат. Если есть уверенность, что начальное расположение объекта близко к искомому, на координаты вершин можно наложить такие ограничения, чтобы вершины не удалялись от начального состояния дальше, чем на некоторую величину dx. Перейдем к описанию общих ограничений g(x). Есть несколько основных групп ограничений для данной задачи, без которых нельзя обойтись. Первой группой таких ограничений являются факты, что вершины должны остаться на своих гранях. Если в грани было три вершины, то заведомо все в порядке. Если больше, требуется наложить ограничения. Условие того, что четыре точки лежат в одной плоскости, равносильно тому, что объем натянутого на них симплекса равен нулю, то есть в нерасписном виде условие выглядит так: x1 – x0, x2 – x0, x3 – x0 = 0, где x0, x1, x2, x3 – точки, лежащие на одной грани. Для лучшей точности это условие необходимо записать для всех четверок вершин во всех гранях, но это сильно замедлит время вычислений солвера, поэтому можно оптимизировать работу исходя из того, что некоторые наборы точек лежат именно в одной грани. Так что, можно в каждой грани брать фиксированные три точки и по очереди добавлять к ним все остальные. Чтобы не возникало пересечения граней по ребрам, которых не должно существовать, необходимо записать условия выпуклости внутреннего многогранника. При данном подходе единственным способом задания ограничений на выпуклость многогранника является выписывание условий локальной выпуклости для каждой из вершин. Для этого необходимо для каждой вершины брать тройки смежных с ней по ребрам вершин и смотреть объем натянутого на них симплекса. Если векторы к этой тройке вершин образуют правую декартову систему координат и начальная вершина является выпуклой, то объем симплекса будет больше нуля, если же точка невыпуклая, то объем отрицательный. Исходя из этого получаются условия x1 – x0, x2 – x0, x3 – x0 ≥ 0, только теперь уже x1, x2, x3 – точки, смежные по ребрам с x0. Если было введено ограничение на сдвиг вершин dx, то для оптимизации по времени эти условия можно записывать только для групп близко лежащих вершин, расстояние между которыми соизмеримо с dx, потому что прочие вершины не смогут достаточно сильно изменить местонахождение в пространстве, чтобы появились невыпуклые дефекты. Последняя группа обязательных условий связана с тем, что внутренний многогранник должен остаться вписанным. Эти условия записываются в следующем виде: Arxj1+Brxj2+Crxj3 – Dr ≤ 0, где r – номер грани внешнего многогранника; j – номер вершины внутреннего многогранника. Стоит заметить, что Ar, Br, Cr, Dr являются константами, а не переменными, а значит, это группа линейных ограничений, незначительно влияющих на время работы солвера. Помимо обязательных ограничений, в зависимости от конкретной задачи могут быть добавлены и другие ограничения, связанные с какими-то размерами многогранника. Но не стоит забывать, что, чем выше степень многочлена, описывающего ограничения, тем сильнее оно замедлит работу солвера. Этот метод неэффективен, потому что возникает очень много сложных ограничений третьего порядка, что значительно замедляет работу солвера. Также возникают сложности с записью дополнительных ограничений, связанных с нормалями граней. Преимуществом данного метода является минимально возможное количество используемых переменных. Это делает матрицы производных меньшего размера, но при этом они менее разреженные. Второй метод Главной идеей второго метода является введение дополнительного набора переменных, отвеча- ющих за параметры граней внутреннего многогранника. Данный подход имеет несколько преимуществ. Во-первых, порядок большей части уравнений в задаче сокращается с третьего на второй, что значительно уменьшает время работы. Во-вторых, уравнения, записанные с использованием двойного набора переменных, более понятны с геометрической точки зрения, что значительно сокращает время отладки алгоритма. В-третьих, существует масса дополнительных ограничений, например, связанных с углами многогранника, которые просто невозможно записать без введения дополнительного набора переменных. Итак, переменные во втором методе будут делиться на два типа. Первый тип – параметры граней внутреннего многогранника yap, ybp, ycp, ydp, где p – номер грани внутреннего многогранника. В качестве ограничений (xU и xL) на переменные первого типа берутся начальные значения параметров плюс/минус некоторая величина соответственно. Размер этой величины зависит от того, насколько разрешается изменять углы нормалей граней заданной комбинаторной структуры. Параметры граней внешнего многогранника не меняются, поэтому рассматриваются как константы. Второй тип переменных – это параметры, отвечающие за расположение вершин внутреннего многогранника в пространстве, xijÎ(–¥, +¥), где j – номер точки; i – ось координат, аналогично первому методу. Ограничения на комбинаторную структуру принимают вид yapxj1 + ybpxj2 + ycpxj3 – ydp = 0, где p – номер грани внутреннего многогранника; j – номер вершины; индексы 1, 2, 3 соответствуют трем осям координат. Рассмотренная группа ограничений записывается для всех пар вершина–грань, для которых верно, что вершина лежит на грани. Перечень всех таких пар получается из начального представления граней многогранника. Ограничения на выпуклость необходимо записать для всех пар вершина–грань внутреннего многогранника, для которых вершина не принадлежит грани: yapxj1 + ybpxj2 + ycpxj3 – ydp ≤ 0. Вычисления на солвере Для вычислений сформулированной НП-задачи автором был использован солвер IPOPT (Internal Point OPTimization) [10]. Он предназначен для поиска локального оптимума в задаче нелинейного программирования методом внутренней точки. Для вычисления солверу необходимо предоставить callback-функции, вычисляющие следующие величины: - значение целевой функции f(x); - градиент целевой функции Ñf(x); - вектор значений вектор-функции ограничений g(x); - якобиан вектор-функции ограничений Ñg(x)T; - гессиан расширенной функции Лагранжа Если для формулировки задачи использовать язык программирования AMPL, то он сам предоставляет эти функции при получении f(x) и g(x). Но AMPL является платным и дорогостоящим для коммерческого использования, поэтому был разработан и реализован интерфейс для работы с солвером Ipopt напрямую, без использования AMPL. Были написаны соответствующие callback-функции, упомянутые выше, для узкого множества функций ограничений. Эти функции имеют вид многочленов третьего порядка:
Матрицы производных для таких ограничений записываются легко в отличие от производных для задачи общего вида. Для базового алгоритма без дополнительных ограничений достаточно такого представления для целевой функции и функций ограничений. Более того, большинство геометрических ограничений могут быть аппроксимированы в таком виде с достаточно хорошей точностью. Дополнительные ограничения В решаемой прикладной задаче очень важна симметрия получаемого решения. Есть несколько групп часто встречаемых дополнительных ограничений, на которых стоит остановиться и пояснить, как их записать в рамках упомянутого интерфейса. Первой такой группой являются ограничения большего, чем третий, порядка. Данная проблема решается методом введения дополнительных переменных, равных произведению двух или трех других, что позволяет понизить порядок уравнений. Ко второй группе отнесем ситуации, когда нужно соотношение двух переменных x/y. Для таких ситуаций необходимо завести переменную z, записать уравнение z*y – x = 0 и использовать z там, где нужно соотношение. Но если это соотношение используется в неравенствах и y имеет непостоянный знак, то Ipopt может некорректно обработать ситуацию. Для симметрии объекта часто необходимо, чтобы в группе каких-то значений ci мало отличались друг от друга. Чтобы не писать для них, что их разница попарно меньше какой-то величины, можно ввести переменные min и max и для всех ci записать следующие уравнения: min < ci; max>ci; max – min Чаще всего, когда нужны дополнительные ограничения, эти ограничения касаются соотношений либо расстояний, либо углов. Формула расстояния от точки до плоскости является уравнением второго порядка, и с ней проблем не возникает. Для расстояний между точками нужна операция взятия корня, которой мы не обладаем. Это решается двумя методами: можно взять расстояние проекции на какую-то ось, которое вычисляется через скалярное произведение, и работать с проекциями либо просто записать уравнения: r>0, r2= (x1–x2)2 + +(y1 – y2)2 + (z1 – z2)2. Так как задача решается численными методами, данные уравнения позволяют использовать r в любых целях, не извлекая корень как таковой вообще. Для ограничений на углы проще всего использовать косинусы углов, вычисляемые через скалярное произведение. Но для очень маленьких углов, а они часто встречаются в условиях жесткой симметрии на азимуты каких-то граней, необходимо использовать синусы углов, поскольку косинус не чувствителен к малым изменениям в районе нуля. Так как sin x ~ x, cos x ~ 1 – x2 в районе нуля, синус вычисляется через векторное произведение, которое также является уравнением третьего порядка. Все эти, казалось бы, элементарные аппроксимации позволяют работать с достаточно большой для прикладных задач точностью, при этом используя только уравнения третьего порядка, что значительно сокращает время работы алгоритма по сравнению с использованием уравнений высокого порядка, корней и обратных тригонометрических функций. Распределенное тестирование Развитие алгоритма требует постоянного тестирования на большом количестве примеров и с различными настройками. Чтобы принять решение о введении новой идеи алгоритма, необходимо запустить многочисленные тесты для выявления слабых мест (то есть ситуации, когда новая идея приводит к замедлению алгоритма или ухудшению качества результата). Для решения этой задачи была создана система удаленного тестирования задачи. На текущий момент система тестирования представляет собой следующее. Для выполнения теста создается его описание в формате json, содержащее полный набор тестовых данных, на которых будет запускаться пробный алгоритм, перечень всех настроечных параметров, ссылки на действующие реализации алгоритма (dll), а также дополнительные файлы, если они могут изменяться. После создания тестового задания оно заносится в очередь. Транспортным каналом передачи данных на сервер является система Dropbox, что очень удобно, так как позволяет следить за ходом работы с широкого спектра мобильных устройств, например с iPad. Далее на тестовом сервере по расписанию запускается скрипт, проверяющий очередь (queue_ starter.py), и, если очередь не пуста и на данный момент сервер свободен, запускается первое задание из очереди. Запуск осуществляется отдельным скриптом (big_button.py). Этот скрипт по полученному тестовому заданию подготавливает все необходимые для запуска данные, после чего параллельно запускает множество процессов с тестируемым приложением на разных данных. Одновременно выполняются по одному процессу на каждом ядре сервера (или по два, если ядра имеют технологию Hyper threading). В случае падения приложения скрипт анализирует уже пройденные тесты и перезапускает приложение заново для продолжения задачи. По окончании работы собирается отчет о результатах в формате json. А далее на его основе формируется удобная для визуального представления результатов таблица в формате Excel. Помимо основного способа формирования отчетов, есть скрипты, которые создают сравнительные таблицы на основании нескольких отчетов. Общая система генерации этих отчетов report.py содержит мини-язык генерации сводных тестируемых параметров. При необходимости можно легко ввести новый параметр, оценивающий работу алгоритма, и вывести его для всех тестов, включая уже пройденные. Например, показать минимальное, максимальное, среднее значения, стандартное отклонение и т.п. Надо заметить, что язык Python очень удобен для написания подобных тестовых систем. По сравнению с языком R, который для таких задачи считается более подходящим, Python оказался предпочтительнее в связи с гибкими возможностями программирования и решением смежных задач – генерацией отчетов. Получившаяся система достаточно стабильна, устойчива к падениям тестируемой системы, позволяет глубоко исследовать результаты тестов и находить неочевидные зависимости. Планируется развитие системы тестирования, которое позволит запускать задания в облаке, что значительно сократит время ожидания масштабных тестов. Результаты Алгоритм был реализован и протестирован на задачах разного размера. Задачи варьировались от простых учебных примеров с простыми, подобными или просто легко вписываемыми многогранниками с количеством вершин меньше пятидесяти до реальных прикладных задач с количеством вершин от ста до пятисот и ограничениями на симметрию разной жесткости. Второй метод на реальных задачах, даже без дополнительных ограничений, работает на порядок быстрее первого, несмотря на увеличенное количество переменных. С учетом этого и удобства записи уравнений он был признан более эффективным. На реальных примерах алгоритм, основанный на втором методе, улучшает любой результат дру- гих алгоритмов в исследуемой прикладной области на 2–5 % объема. Основные тестируемые примеры содержали вписываемый многогранник с количеством вершин и граней порядка 150 и внешний многогранник с количеством вершин и граней порядка 500, общее количество ограничений порядка 10 000. Время построения задачи на этих примерах составляет около одной секунды. Время вычисления на солвере без ограничений на симметрию ~5 секунд. Время вычислений на солвере с ограничениями на симметрию – 20–40 секунд в зависимости от жесткости ограничений. В своей работе Ipopt использует различные библиотеки для решения систем линейных уравнений и BLAS’ы (библиотеки базовых операций линейной алгебры). Были проведены эксперименты по запуску алгоритма на разных сборках Ipopt, включающих в себя разные комбинации библиотек. Некоторые из этих библиотек могут работать в многопоточном режиме, поэтому отличается еще и количество потоков. Тестирование показало, что наиболее быстрыми оказались сборки, использующие библиотеку МА57. Таким образом, в статье рассмотрены два варианта алгоритма вписывания одного многогранника в другой и приведена их сравнительная характеристика. Предложены готовые программные продукты, которые значительно упрощают написание данного алгоритма. Рассмотрены возможные способы оптимизации времени работы алгоритма, варианты его модификаций в зависимости от прикладной задачи, основные идеи упрощения огра- ничений. Алгоритм протестирован на реальных данных, получены хорошие результаты по качеству и времени работы. Алгоритм является эффективным и актуальным, потому что за счет сведения к НП-задаче можно распараллелить вычисления, что крайне важно с учетом развития современных вычислительных технологий. Приведена эффективная система тестирования алгоритма в распределенной среде. Литература 1. Tarasov A., Musin O. The strong thirteen spheres problem. Discrete Comput. Geom., 2012, vol. 48, pp. 128–141. 2. Мусин О.Р. Проблема двадцати пяти сфер // Успехи матем. наук. 2003. Т. 58. № 4 (352). С. 153–154. 3. Hales T. The status of the Kepler conjecture. Mathematical Intelligencer, 1994, no. 16, pp. 47–58. 4. Валиахметова Ю.И., Филиппова А.С. Теория оптимального использования ресурсов Л.В. Канторовича в задачах раскроя-упаковки: обзор и история развития методов решения // Вестн. УГАТУ. 2014. Т. 18. № 1 (62). 5. Афанасьев А.П., Волошинов В.В., Лисов А.А., Наумцева А.К. Организация распределенной обработки данных с помощью RESTful-веб-сервисов // Современные проблемы науки и образования: Технические науки. 2012. № 6. C. 31. 6. Волошинов В.В., Смирнов С.А. Принципы интеграции программных ресурсов в научных вычислениях // Информационные технологии и вычислительные системы. 2012. № 3. С. 66–71. 7. Кокорев Д.С. Алгоритм поиска выпуклого многогран- ника максимального объема, вписанного в другой многогранник // Информационные технологии и вычислительные системы. 2013. № 3. С. 27–31. 8. Емеличев В.А., Ковалев М.М., Кравцов М.К. Многогранники, графы, оптимизация. М.: Наука, 1981. 346 с. 9. Fourer R., Gay D.M., and Kernighan B.W. AMPL: A Modeling Language for Mathematical Programming, Duxbury Press, 2002, 540 p. 10. Kawajir Y., Laird C., Wächter A. Introduction to Ipopt: A tutorial for downloading, installing, and using Ipopt, 2010. URL: http://www.coin-or.org/Ipopt/documentation/ (дата обращения: 10.10.2014). |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=4115&lang= |
Версия для печати Выпуск в формате PDF (8.31Мб) Скачать обложку в формате PDF (1.24Мб) |
| Статья опубликована в выпуске журнала № 1 за 2016 год. [ на стр. 90-95 ] |
Назад, к списку статей



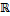 n – оптимизационные переменные с верхними и нижними ограничениями:
n – оптимизационные переменные с верхними и нижними ограничениями: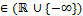 n, xU
n, xU 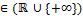 n;
n;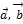 ,
, 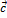 ) векторов
) векторов 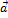 на векторное произведение векторов
на векторное произведение векторов  и
и 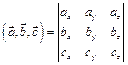 .
.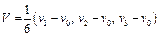 , где vi – векторы координат вершин симплекса.
, где vi – векторы координат вершин симплекса.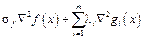 .
.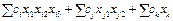 .
.