В связи с увеличением объемов выдачи кредитов банками появились так называемые системы кредитного скоринга – автоматизированные системы, основанные на применении математического аппарата и направленные на минимизацию кредитных рисков при кредитовании клиентов. Основными задачами этих систем являются оценка или прогноз кредитоспособности и платежеспособности клиентов банка на основе анкетных данных, сведений, запрашиваемых из бюро кредитных историй, а также любой другой информации, которую может иметь банк [1, 2]. Однако, как показывает практика, рост задолженностей и невозврата по кредитам, а также конкуренция на рынке кредитных услуг требуют совершенствования существующих методов и алгоритмов прогнозирования.
Предлагается система прогнозирования платежеспособности клиентов банка, состоящая из двух подсистем: подсистемы прогнозирования кредитоспособности клиентов (анкетный скоринг) и подсистемы прогнозирования изменения платежеспособности заемщиков (поведенческий скоринг). Первая подсистема реализует процедуру моделирования и прогнозирования выдачи кредита с использованием агрегированных классификаторов (АК), полученных на основе методов машинного обучения [3], вторая – процедуру моделирования и прогнозирования погашения кредита с использованием марковских цепей 1-го и 2-го порядков, а также методов машинного обучения. На рисунке 1 представлена структурная схема системы прогнозирования платежеспособности клиентов банка.

АК на основе методов машинного обучения
Для прогнозирования кредитоспособности клиентов применяются АК, представляющие собой объединенные результаты следующих методов машинного обучения [4]: нейронная сеть (НС), логистическая регрессия (ЛР), дискриминантный анализ (ДА), наивный байесовский классификатор (НБК), метод опорных векторов (МОВ), деревья решений (ДР) и бэггинг деревьев решений (БДР).
Для нахождения оптимальных АК используется метод полного перебора всевозможных наборов перечисленных выше базовых моделей. Таким образом, первый АК состоит из всех семи базовых классификаторов, второй – из шести различных базовых классификаторов и т.д., последний АК состоит из двух различных базовых классификаторов.
Для формирования единого решения о кредитоспособности клиента на основе отдельных методов классификации осуществляется объединение результатов одним из трех способов: по среднему значению, по медиане, а также с помощью процедуры голосования.
Пусть 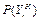 – вероятность кредитоспособно- сти r-го клиента, найденная с помощью К-го базового классификатора, причем r=1, ..., l, K=1, ..., H, где l – количество клиентов, H – количество базовых классификаторов в наборе. Тогда получим следующие АК.
– вероятность кредитоспособно- сти r-го клиента, найденная с помощью К-го базового классификатора, причем r=1, ..., l, K=1, ..., H, где l – количество клиентов, H – количество базовых классификаторов в наборе. Тогда получим следующие АК.
АК по среднему значению:
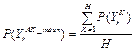 , где
, где 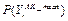 – вероятность кредитоспособности r-го клиента, найденная с помощью АК по среднему значению.
– вероятность кредитоспособности r-го клиента, найденная с помощью АК по среднему значению.
АК по медиане: для начала следует ранжировать ряд, содержащий результаты базовых классификаторов в каждом наборе. В случае нечетного числа базовых классификаторов вероятность кредитоспособности r-го клиента, полученная с помощью АК по медиане  находится следующим образом:
находится следующим образом: 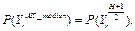
В случае четного числа базовых классификаторов вероятность кредитоспособности r-го клиента находится путем вычисления половины суммы результатов срединных базовых классификаторов.
Результат АК по голосованию представляет собой среднее значение результатов базовых классификаторов, которые определили кредитоспо- собность клиента c вероятностью P(YK)³0,1. В противном случае вероятность кредитоспособности клиента равна нулю 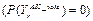 .
.
Совместное использование нескольких методов классификации позволяет выделить следующие преимущества: при рассмотрении каждого классификатора как процедуры поиска наилучшей гипотезы о распределении клиентов на классы кредитоспособности объединение результатов нескольких классификаторов по среднему значению позволяет усреднить ошибку каждой отдельной гипотезы; при использовании нескольких методов классификации происходит расширение множества возможных гипотез и уменьшение влияния различных случайностей при определении гипотез; при использовании таких методов классификации, как НС и ДР, есть вероятность «застрять» в локальном мини- муме, а при использовании агрегирования результатов существует больше возможностей для нахождения глобального минимума.
Подсистема оценки кредитоспособности клиентов
При принятии решения о выдаче кредита данная подсистема прогнозирует кредитоспособность потенциального заемщика банка с помощью АК на основе анкетных данных клиента (возраст, пол, семейное положение, сумма кредита, информация о доходах и расходах и т.д.), а также визуализирует полученные результаты и сохраняет их в файл электронных таблиц Excel.
Поскольку в реальных статистических данных приходится сталкиваться с рядом проблем [5], перед моделированием проводятся предварительный анализ и обработка исходных данных по клиентам: кодирование нечисловых данных, дискретизация непрерывных данных методом биннинга [6], а также отбор наиболее информативных признаков с помощью пошаговой регрессии [7].
Далее исходная выборка, представляющая собой анкетные данные по «старым» заемщикам, а также класс кредитоспособности, делится на обучающую и тестовую части. Обучающая выборка предназначена, как правило, для построения различных классификаторов, а тестовая используется для прогнозирования и оценки качества классификаторов. При этом для получения более адекватных и несмещенных оценок процедура разделения исходной выборки на обучающую и тестовую части повторяется 10 раз в произвольном порядке. Затем результаты прогнозирования, полученные на контрольных выборках, усредняются. Данная процедура называется 10-кратной перекрестной проверкой [8].
Критерием качества работы классификаторов является дисперсия ошибки прогнозирования s2, показывающая отклонение фактической вероятно- сти принадлежности к классу кредитоспособности r-го клиента P(Yr) от прогнозируемой вероятности принадлежности к классу кредитоспособности r-го клиента  , которая стремится к минимальному значению для заданного числа клиентов l:
, которая стремится к минимальному значению для заданного числа клиентов l: 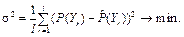
Для каждой модели предлагается оптимальный порог классификации клиентов на классы кредитоспособности, который находится с помощью решения задачи минимизации ошибок первого и второго рода (ошибок построения моделей).
Ошибка первого рода возникает, когда интересующее нас событие ошибочно не обнаружилось, то есть это количество кредитоспособных клиентов, классифицированных как некредитоспособные (lgb). По сути ошибка первого рода характеризует коммерческий риск χ1, связанный с отказом кредитоспособным клиентам:  где lgg – количество верно классифицированных кредитоспособных клиентов.
где lgg – количество верно классифицированных кредитоспособных клиентов.
Ошибка второго рода возникает, когда при отсутствии события ошибочно выносится решение о его присутствии, то есть это количество некредитоспособных клиентов, классифицированных как кредитоспособные (lbg). Ошибка второго рода характеризует так называемый кредитный риск χ2: 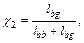 где lbb – количество верно классифицированных некредитоспособных клиентов.
где lbb – количество верно классифицированных некредитоспособных клиентов.
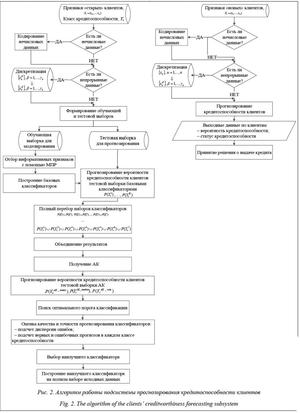 С помощью наилучшей модели и оптимального порога классификации осуществляется прогноз кредитоспособности «новых» клиентов. На рисунке 2 показан алгоритм работы подсистемы оценки кредитоспособности клиентов.
С помощью наилучшей модели и оптимального порога классификации осуществляется прогноз кредитоспособности «новых» клиентов. На рисунке 2 показан алгоритм работы подсистемы оценки кредитоспособности клиентов.
Марковские цепи и методы машинного обучения
Математические модели для описания динамики погашения по кредитам на основе марковских цепей 1-го и 2-го порядков, позволяющие учитывать прошлые состояния кредитной истории [9], имеют следующий вид:
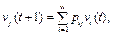
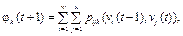
где vi(t) – вероятность того, что кредитный счет окажется в состоянии Si в момент времени t; pij(t) – вероятность перехода счета из состояния Si в момент времени t в состояние Sj за один шаг; w – количество состояний; φi(t) – вероятность того, что счет окажется в состоянии Sk в момент времени t, если предыдущими состояниями были Si и Sj; pijk(t) – вероятность перехода счета в состояние Sk, если предыдущими состояниями были Si в момент времени t–1 и Sj в момент времени t.
При этом в качестве состояний S1, …, Sw используется информация о просроченной задолженности по кредитным счетам заемщиков.
Для оценки переходных вероятностей предложено использовать различные методы машинного обучения, которые позволяют учитывать признаки, предположительно, влияющие на платежеспособность заемщика (условия кредита и информацию о самом заемщике). Например, зависимости между оценками переходных вероятностей для марковской цепи 1-го и 2-го порядков 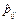 и
и  , а также признаками
, а также признаками 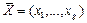 на основе дискриминантного анализа имеют следующий вид:
на основе дискриминантного анализа имеют следующий вид:
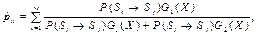

где P(Si® Sj), P(Si®Sj®Sk) – априорные вероятности перехода счета из состояния Si в состояние Sj и из состояния Si в состояние Sk соответственно; 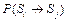 ,
, 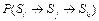 – априорные вероятности отсутствия перехода счета из состояния Si в состояние Sj и из состояния Si в состояние Sk соответственно; G1(Х), G2(Х) – плотности распределения признаков
– априорные вероятности отсутствия перехода счета из состояния Si в состояние Sj и из состояния Si в состояние Sk соответственно; G1(Х), G2(Х) – плотности распределения признаков 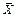 , подчиняющиеся нормальному закону распределения.
, подчиняющиеся нормальному закону распределения.
На основе ДР для каждого перехода Si®Sj и Si®Sj®Sk строится свое ДР (рис. 3).

Поскольку зависимости между оценками переходных вероятностей, а также признаками, предположительно, влияющими на платежеспособность заемщиков, предназначены для конкретного перехода из одного состояния кредитного счета в другое, предлагается выбор наилучшей модели для каждого перехода, что повышает общую точность прогнозирования по всем переходам.
Подсистема прогнозирования изменения платежеспособности заемщиков
При погашении кредита заемщиком данная подсистема прогнозирует изменение платежеспособности заемщика с помощью марковских цепей и методов машинного обучения на основе анкетных данных клиента, кредитной истории, а также условий взятия кредита.
Перед моделированием также проводятся предварительный анализ и обработка исходных данных по клиентам, в том числе восстановление пропущенных данных кредитной истории с использованием условного распределения по присутствующим параметрам [10].
Оценка качества прогнозирования моделей осу- ществляется на тестовой выборке, содержащей данные по заемщикам в момент времени (t+1), которые не участвовали в процессе построения моделей. Основным критерием качества прогнозирования является доля верных прогнозов, усредненная по всем состояниям ε:  где daa – количество верных прогнозов для кредитных счетов, находящихся в состоянии Sα, a=1, ..., w; da1+ ...+ daw – общее количество прогнозов для кредитных счетов, находящихся в состоянии Sα.
где daa – количество верных прогнозов для кредитных счетов, находящихся в состоянии Sα, a=1, ..., w; da1+ ...+ daw – общее количество прогнозов для кредитных счетов, находящихся в состоянии Sα.
На рисунке 4 показан алгоритм работы подсистемы прогнозирования изменения платежеспособности заемщиков.
Численное исследование
Для проверки разработанной системы проведен эксперимент, в котором в качестве исходных данных использовались данные по российским клиентам (данные предоставлены международной компанией по анализу и обработке данных АлгоМост в 2015 г. и находятся в открытом доступе: http://algomost.com/ru/tasks/uploadfiles/58/train_utf_noid.sas7bdat, а также банком Тинькофф в 2013 г. и находятся в открытом доступе: https://static.tcsbank. ru/documents/olymp/SAMPLE_CUSTOMERS.csv).
С помощью подсистемы прогнозирования кредитоспособности клиентов были построены базовые классификаторы и АК, а также найдены наилучшие классификаторы для трех случаев: на полном наборе исходных данных, при отборе информативных признаков, а также при отборе информативных признаков совместно с процедурой дискретизации. В качестве примера на рисунке 5 представлены результаты построения моделей прогнозирования кредитоспособности клиентов при отборе информативных признаков.
В таблице 1 показаны усредненные результаты расчета дисперсии ошибок прогнозирования классификаторов для всех трех случаев.
Согласно результатам расчета дисперсии ошибок прогнозирования кредитоспособности российских заемщиков, а также результатам прогнози- рования при нахождении оптимального порога классификации, использование АК увеличивает точность прогнозирования во всех трех случаях: на полном наборе исходных данных, при отборе информативных признаков, а также при отборе информативных признаков совместно с процедурой дискретизации. При этом наилучший результат достигается с использованием АК при отборе информативных признаков и представляет собой объединение результатов по голосованию ЛР и БДР (табл. 2).
Таблица 1
Значения дисперсии ошибок прогнозирования
Table 1
The values of a forecasting mean square error
|
Классификатор
|
Полная исходная выборка
|
Информативные признаки
|
Дискретизация и информативные признаки
|
|
НС
|
0,2523
|
0,2469
|
0,2513
|
|
ДА
|
0,2533
|
0,2435
|
0,2445
|
|
БК
|
0,3671
|
0,3121
|
0,2955
|
|
МОВ
|
0,2466
|
0,2449
|
0,2448
|
|
ДР
|
0,3796
|
0,3544
|
0,3290
|
|
ЛР
|
0,2457
|
0,2431
|
0,2439
|
|
БДР
|
0,2278
|
0,2206
|
0,2595
|
|
АК
|
0,22721
|
0,21872
|
0,24363
|
Таблица 2
Максимальные значения дисперсии ошибок
Table 2
The maximum values of forecasting error mean square
|
АК
|
Способ объединения результатов
|
Состав АК
|
|
0,22721
|
По медиане
|
ДР + ЛР + БДР
|
|
0,21872
|
По голосованию
|
ЛР + БДР
|
|
0,24363
|
По медиане
|
ДА + ЛР + БДР
|
В случае оптимального порога классификации, который равен 0,499, наилучший АК представляет собой объединение результатов по голосованию НС и БДР. При этом сумма ошибок I и II рода АК по сравнению с отдельными базовыми классификаторами уменьшилась на 0,8–22,2 %.
Для прогнозирования кредитоспособности «новых» клиентов имеет смысл использовать один из наилучших классификаторов, выбор которого зависит от политики кредитования банка.


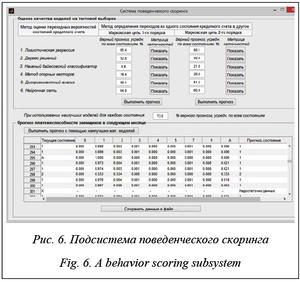 С использованием подсистемы прогнозирования изменения платежеспособности заемщиков были построены модели описания динамики погашения кредитов, а также найдены наилучшие модели для конкретного перехода из одного состояния кредитного счета в другое (рис. 6). В таблице 3 представлены результаты верных прогнозов для каждой модели и марковской цепи 1-го и 2-го порядков по всем возможным переходам из отдельного состояния Si в другие состояния, средний результат (Ср.) по всем состояниям, а также максимальные значения (Макс.) для каждого состояния, выраженные в процентах.
С использованием подсистемы прогнозирования изменения платежеспособности заемщиков были построены модели описания динамики погашения кредитов, а также найдены наилучшие модели для конкретного перехода из одного состояния кредитного счета в другое (рис. 6). В таблице 3 представлены результаты верных прогнозов для каждой модели и марковской цепи 1-го и 2-го порядков по всем возможным переходам из отдельного состояния Si в другие состояния, средний результат (Ср.) по всем состояниям, а также максимальные значения (Макс.) для каждого состояния, выраженные в процентах.
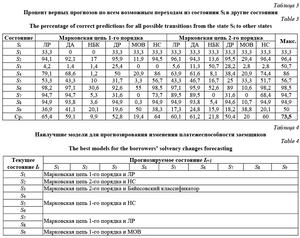
Результаты исследования показали, что нет единой модели, наилучшим образом прогнозирующей все переходы из состояния Si в другие состояния. Для прогнозирования изменения платежеспособности заемщиков в следующем периоде оптималь- ным вариантом является выбор наилучшей марковской цепи и модели для каждого перехода, что в среднем улучшает результаты отдельных моделей от 7,6 до 63 % (табл. 4).
Таким образом, как показывает проведенное численное исследование, предложенные методы и алгоритмы улучшают качество прогнозирования кредитоспособности и изменения платежеспособности заемщиков. Следовательно, разработанная система может быть использована для поддержки принятия решений в процессе кредитования клиентов банками, начиная с процесса выдачи кредита и до последующего погашения по текущим кредитным платежам.
Литература
1. Литвинова С.А. Скоринговые системы как средство минимизации кредитного риска банка // Аудит и финансовый анализ. 2010. № 2. С. 396–397.
2. Глинкина Е.В. Кредитный скоринг как инструмент эффективной оценки кредитоспособности // Финансы и кредит. 2011. № 16 (448). С. 43–47.
3. Шунина Ю.С., Алексеева В.А., Клячкин В.Н. Прогнозирование кредитоспособности клиентов банка на основе мето- дов машинного обучения // Финансы и кредит. 2015. № 27 (651). С. 2–12.
4. Мерков А.Б. Распознавание образов: введение в методы статистического обучения. М.: URSS, 2010. 254 с.
5. Гринь Н.В. Методологические аспекты построения скоринговых моделей // Экономика, моделирование, прогнозирование: сб. науч. тр. Вып. 6. Минск: Изд-во НИЭИ Минэкономики РБ, 2012. С. 174–180.
6. Сорокин А.С. Построение скоринговых карт с использованием модели логистической регрессии // Науковедение. 2014. № 2 (21). URL: http://naukovedenie.ru/PDF/180EVN214.pdf (дата обращения: 12.09.2015).
7. Дрейпер Н., Смит Г. Прикладной регрессионный анализ. М.: Диалектика, 2007. 912 c.
8. Вежневец В. Оценка качества работы классификаторов // Компьютерная графика и мультимедиа. 2006. № 4. URL: http://cgm.computergraphics.ru/content/view/106 (дата обращения: 12.09.2015).
9. Соколов Г.А., Чистякова Н.А. Теория вероятностей. Управляемые цепи Маркова в экономике. М.: Физматлит, 2005. 248 с.
10. Алексеева В.А., Донцова Ю.С., Клячкин В.Н. Восстановление пропущенных наблюдений при классификации объектов // Изв. Самарского науч. центра РАН. 2014. Т. 16. № 6 (2). С. 357–359.




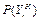 – вероятность кредитоспособно- сти r-го клиента, найденная с помощью К-го базового классификатора, причем r=1, ..., l, K=1, ..., H, где l – количество клиентов, H – количество базовых классификаторов в наборе. Тогда получим следующие АК.
– вероятность кредитоспособно- сти r-го клиента, найденная с помощью К-го базового классификатора, причем r=1, ..., l, K=1, ..., H, где l – количество клиентов, H – количество базовых классификаторов в наборе. Тогда получим следующие АК.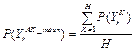 , где
, где 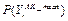 – вероятность кредитоспособности r-го клиента, найденная с помощью АК по среднему значению.
– вероятность кредитоспособности r-го клиента, найденная с помощью АК по среднему значению. находится следующим образом:
находится следующим образом: 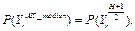
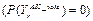 .
. , которая стремится к минимальному значению для заданного числа клиентов l:
, которая стремится к минимальному значению для заданного числа клиентов l: 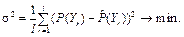
 где lgg – количество верно классифицированных кредитоспособных клиентов.
где lgg – количество верно классифицированных кредитоспособных клиентов.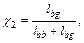 где lbb – количество верно классифицированных некредитоспособных клиентов.
где lbb – количество верно классифицированных некредитоспособных клиентов.
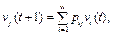
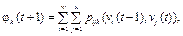
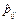 и
и  , а также признаками
, а также признаками 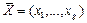 на основе дискриминантного анализа имеют следующий вид:
на основе дискриминантного анализа имеют следующий вид: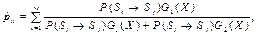

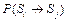 ,
, 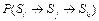 – априорные вероятности отсутствия перехода счета из состояния Si в состояние Sj и из состояния Si в состояние Sk соответственно; G1(Х), G2(Х) – плотности распределения признаков
– априорные вероятности отсутствия перехода счета из состояния Si в состояние Sj и из состояния Si в состояние Sk соответственно; G1(Х), G2(Х) – плотности распределения признаков 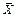 , подчиняющиеся нормальному закону распределения.
, подчиняющиеся нормальному закону распределения.
 где daa – количество верных прогнозов для кредитных счетов, находящихся в состоянии Sα, a=1, ..., w; da1+ ...+ daw – общее количество прогнозов для кредитных счетов, находящихся в состоянии Sα.
где daa – количество верных прогнозов для кредитных счетов, находящихся в состоянии Sα, a=1, ..., w; da1+ ...+ daw – общее количество прогнозов для кредитных счетов, находящихся в состоянии Sα.



