Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Пчелиный алгоритм оптимизации для решения задачи планирования беспроводной сети
Аннотация:Статья посвящена решению проблемы планирования беспроводной сети. В ней сформулирована задача размещения базовых станций, учитывающая межсотовые помехи, затухание при распространении сигнала, несколько типов базовых станций. Решение задачи представляется в виде массива структур, хранящих информацию об одном местекандидате (тип установленной базовой станции, список подключенных к ней клиентов). Разработана модификация одного из метаэвристических методов – пчелиного алгоритма BCO (Bee Colony Optimization). Метод оптимизации подражанием пчелиной колонии относится к мультиагентным методам, основанным на моделировании интеллектуального поведения колоний агентов, так называемым методам роевого интеллекта. В природе подобным интеллектом обладают группы общественных насекомых, например, колонии муравьев, пчел, термитов. В основе предлагаемого алгоритма лежит понятие окрестности текущего решения. Для формирования окрестности используются небольшие операции по изменению текущей конфигурации беспроводной сети. Новое решение из окрестности текущего может быть получено при помощи одной из двух операций: смена типа одной станции на более дешевый, удаление одной базовой станции. Новый алгоритм реализован как ПО в среде разработки Delphi. Показано, что пчелиный алгоритм позволяет находить решение задачи размещения базовых станций за приемлемое время, на много порядков быстрее точного метода полного перебора. Выявлена зависимость качества решения поставленной задачи методом подражания пчелиной колонии от значений управляющих параметров алгоритма.
Abstract:The article is devoted to solving a wireless network planning task. The authors defined the problem of base stations’ location, taking into account the level of attenuation of signal during propagation, the level of inter -cell interference and several types of base stations. A problem solution is represented as a vector of structures, each structure stores data about one potential site (an installed base station type, a list of connected clients). A modification of one of metaheuristic methods (bee colony optimization algorithm) has been developed. The bee colony optimization method is a multi-agent method based on simulation of intelligent behavior of agent colonies (the so-called swarm intelligence methods). Naturally, some groups of social insects (for example, colonies of ants, bees, termites) have such intellect. The proposed algorithm is based on the concept of current solution neighborhood. Little changes in current wireless network configuration are used to form the neighborhood. To obtain a new solution from the neighborhood of the current solution we can use one of the following two operations: changing the type of a station to more cheap or removing a base station. The developed algorithm is implemented in Delphi programming environment. The article shows that the new algorithm helps to find the solution for the base station location problem in a reasonable time, much faster than the exact method of exhaustive search. The authors found out how the quality of the problem solution obtained by bee colony optimization algorithm depends on values of control parameters.
| Авторы: Скаков Е.С. (wallkirya@mail.ru) - Липецкий государственный педагогический университет (аспирант), Липецк, Россия, Малыш В.Н. (vmalysh@mail.ru) - Липецкий филиал Российской академии народного хозяйства и государственной службы при Президенте Российской Федерации (профессор), Липецк, Россия, доктор технических наук | |
| Ключевые слова: размещение базовых станций, пчелиный алгоритм, беспроводные сети, оптимизация, sir |
|
| Keywords: base station location, bee colony optimization, wireless network, optimisation, sir |
|
| Количество просмотров: 12618 |
Версия для печати Выпуск в формате PDF (6.81Мб) Скачать обложку в формате PDF (0.36Мб) |
Важным этапом при проектировании беспроводной сети передачи данных является синтез ее топологической структуры. Он подразумевает планирование территориального размещения базовых приемо-передающих станций и подключение к ним клиентов. Отметим работы [1] и [2], посвященные проблеме размещения базовых станций (БС) в сетях стандарта WiMAX. Статья [3] посвящена классификации алгоритмов размещения БС в сетях стандарта UMTS. В данной статье сформулирована задача размещения БС (ЗРБС), в основе которой лежит математическая модель, учитывающая уровень SIR для клиентов, уровень затухания сигнала при распространении от клиента к БС и обратно, наличие в сети нескольких типов БС. Сформулированная задача решается при помощи метаэвристического пчелиного алгоритма оптимизации, который демонстрирует высокую точность и скорость нахождения решений. Постановка задачи размещения БС ЗРБС формулируется следующим образом. Пусть есть некоторое множество клиентов (Ntp штук). Все клиенты должны быть подключены к БС, причем есть заранее определенное множество (Nps штук) потенциальных мест, куда может быть установлена БС (так называемых мест-кандидатов). Для установки доступны БС нескольких ти- пов (Ntypes типов), отличающихся по своим характе- ристикам. При этом должен выполняться ряд тре- бований и ограничений [4]. Для описания решения ЗРБС воспользуемся такой единицей представления данных, как структура. Структура представляет собой композитный тип данных, который позволяет хранить набор переменных различного типа (т.н. полей), объединенных одним именем [5]. Для ЗРБС структура состоит из трех полей: - целочисленная переменная type, отражающая тип БС, установленной на данном месте (считается, что БС не установлена, если type = 0); - целочисленная переменная cl_nbr, отражающая число клиентов, подключенных к данному месту-кандидату; - вектор (одномерный массив) целых чисел CL размерности cl_nbr, содержащий номера клиентов, подключенных к данному месту-кандидату. Решение ЗРБС представляет собой вектор Sol, каждый элемент которого является структурой, соответствующей одному месту-кандидату (пояснение: здесь и в дальнейшем запись вида Arr[j] означает обращение к j-му элементу вектора Arr; элементы массивов нумеруются, начиная с 1). Обращение к полю структуры обозначается символом «.». То есть Sol[5].type означает тип БС пятого места-кандидата, а, например, Sol[3].CL[2] означает номер 2-го клиента, подключенного к станции на месте № 3. Клиента можно подключить к месту-кандидату, только если на нем уже установлена БС, то есть для места, у которого Sol[s].cl_nbr ≠ 0, должно выполняться Sol[s].type ≠ 0. Пусть b – вектор, содержащий значения требуемых полос пропускания для клиентов; β – вектор производительностей БС разного типа. Для каждой БС трафик всех клиентов не должен превышать значения производительности станции:
Пусть Для режима downlink существует мощностное ограничение. Мощность, дошедшая к клиенту от БС, несмотря на затухание сигнала, должна превышать минимальную целевую мощность:
Мощностное ограничение для режима uplink:
Минимизируемая целевая функция имеет вид
где Cost – массив стоимостей БС разного типа. Первое слагаемое формулы (4) – стоимость оборудования. Второе слагаемое учитывает уровень SIR для клиентов беспроводной сети. SIR (signal-to-interference ratio) – отношение уровня сигнала к уровню помех [6], рассчитываемое следующим образом: В формуле (4) SIR рассчитывается для каждого клиента отдельно. Числитель содержит сигнал, дошедший от той БС, к которой подключен клиент, в знаменателе фигурируют сигналы от остальных БС, создающие помехи:
где wsiqz = 0, если s = q и i = z, иначе wsiqz = 1. Коэффициент k отвечает за одновременный учет в целевой функции затрат на создание комплекса БС и уровня межсотовых помех для клиентов. k должен иметь размерность стоимости БС, обеспечивая сохранение размерности в формуле (4), так как SIR – безразмерная величина. Коэффициент k должен обеспечивать «штраф» за низкий уровень SIR и «награду» за высокий. В данной статье принято, что k=–10 условных единиц стоимости (k должен быть отрицательным, так как ЗРБС – минимизационная задача, а значит, высокий уровень SIR должен уменьшать целевую функцию). Отсортируем типы БС по возрастанию стоимости, то есть сделаем так, что i-й тип БС дороже (i–1)-го и дешевле (i+1)-го. Общие сведения о роевом интеллекте Метод оптимизации подражанием пчелиной колонии относится к мультиагентным методам, основанным на моделировании интеллектуального поведения колоний агентов, так называемым методам роевого интеллекта (Swarm Intelligence). В природе подобным интеллектом обладают группы общественных насекомых, например колонии муравьев, пчел, термитов [7]. Другие названия метода оптимизации подражанием пчелиной колонии – пчелиный алгоритм, метод/алгоритм пчелиного роя, метод/алгоритм пчелиной колонии. В настоящей статье для обозначения данного класса метаэвристик будет использоваться словосочетание «пчелиный алгоритм». Отметим некоторые особенности роевого интеллекта. Каждый из агентов роя характеризуется стохастическим поведением на основе собственного восприятия окрестности. Агенты руководствуются локальными правилами, не имея никакого представления о глобальной цели. Взаимодействие между подобными самоорганизующимися агентами приводит к появлению некой формы коллективного разума под названием роевой интеллект [8]. Особи, входящие в рой, коллективно используют окружающую среду и ресурсы. Ключевой особенностью роевой системы является самоорганизация: низкоуровневые взаимодействия (так называемый микроскопический уровень) приводят к изменениям на глобальном (макроскопическом) уровне [8]. Под самоорганизацией роя в [9] подразумеваются следующие четыре особенности. 1. Положительная обратная связь. Например, на основе уровня концентрации феромона, отложенного другими муравьями, муравей выбирает себе путь от муравейника до источника питания (чем выше уровень феромона на тропе, тем с большей вероятностью муравей выберет эту тропу). 2. Отрицательная обратная связь. Уравновешивает положительную обратную связь и помогает стабилизировать коллективный шаблон поведения. Например, на основе информации от других пчел пчела может решить, что ее текущий источник нектара значительно хуже других найденных источников, и оставить этот источник. 3. Случайность. Флуктуации (случайные блуждания, ошибки, вероятностный поиск) очень важны для функционирования роевого интеллекта, так как позволяют рою находить новые решения. 4. Множественность взаимодействия. Агенты роя используют информацию, поступающую от других агентов, таким образом, данные об окружающей среде распространяются по всему рою. Особенности самоорганизации, отмеченные в [9], четко прослеживаются в пчелиных роях, однако решение оптимизационных задач на основе подражания поведению пчел – довольно молодая дисциплина: первые работы, посвященные пчелиному алгоритму, датированы началом 2000-х годов. Биологические основы пчелиного алгоритма Пчелы в природе ищут пищу путем изучения пространства в окрестности их улья. Как правило, на начальной стадии несколько пчел-разведчиков исследуют окружающую среду. По завершении поиска пчелы-разведчики возвращаются в улей и информируют других членов роя о месте, количестве и качестве доступных источников питания, которые были найдены ими. Обмен информацией происходит при помощи танца на специально отведенной для этого площадке. Если пчела, наблюдавшая танцы скаутов, решает покинуть улей и собирать нектар, она будет следовать за одним из разведчиков к одному из ранее обнаруженных источников пищи. Такая пчела становится занятым фуражиром. Она занимается сбором нектара, при этом уточняя информацию о количестве нектара в окрестности найденного источника. После сбора фуражир возвращается в улей и оставляет там собранный нектар. Затем он может совершить одно из следующих действий [10]: - стать незанятым фуражиром, оставив свой текущий источник нектара; - продолжить добывать нектар из своего источника, не вербуя незанятых пчел посредством танца; - продолжить добывать нектар из своего источника, при этом вербуя незанятых пчел. Описанный процесс продолжается непрерывно, в то время как улей накапливает нектар и исследует новые области с потенциальными источниками питания. Алгоритм BCO На данный момент одной из самых популярных концепций роевого интеллекта является метод BCO (Bee Colony Optimization), предложенный в начале 2000-х годов [11]. Подробное описание алгоритма и его возможных разновидностей приведено в работах [10] и [12]. В данной статье рассматривается модифицированный алгоритм BCO (variant of BCO based on the improvement concept, BCOi) [13]. Особенностью BCOi является то, что рассматривается работа с полными (завершенными) решениями оптимизационной задачи, а не с частичными, как в классическом BCO. Во всех разновидностях пчелиного алгоритма решение оптимизационной задачи рассматривается как источник нектара. Очевидно, что количество нектара в источнике пропорционально качеству представляющего его решения. В случае минимизационной задачи полезность источника нектара обратно пропорциональна значению целевой функции решения. В алгоритме BCOi популяция агентов (искусственных пчел) состоит из B особей, совместно ищущих оптимальное решение. Каждая пчела ответственна за одно решение задачи. Имеются две чередующиеся фазы поиска: прямой проход (forward pass) и обратный проход (backward pass), которые вместе составляют один шаг алгоритма BCO [10–13]. В процессе прямого прохода каждая пчела исследует пространство поиска. Исследование под- разумевает заданное число шагов по улучшению решения. Поиск осуществляется в окрестности текущего решения. В результате исследования получается новое решение. Отметим, что для расширения пространства поиска авторы работ [10–13] предлагают не выбирать лучшее решение в окрестности, а производить так называемую пропорциональную селекцию (другое название – метод рулетки). Данный метод для задач минимизации может быть кратко описан следующим образом: «Если значение целевой функции i-го решения в k раз меньше значения целевой функции j-го решения, то вероятность выбора i-го решения в качестве нового решения должна быть в k раз больше, чем аналогичная вероятность для j-го решения». После получения новых решений начинается второй этап – обратный проход. В процессе обратного прохода все искусственные пчелы обмениваются информацией о качестве «своих» решений, то есть о вычисленных значениях целевой функции. Когда обмен информацией полностью завершен, каждая пчела решает (с определенной вероятностью), стоит ли ей отказаться от своего источника нектара. Пчелы, ассоциированные с лучшими решениями, имеют лучшие шансы на то, чтобы сохранить свои текущие решения и «разрекламировать» их среди других пчел. R пчел, сохраняющих свои решения, в BCOi называются рекрутами. Если пчела отказывается от своего текущего решения, то она должна выбрать одно из решений, предлагае- мых другими пчелами. Очевидно, что у лучших решений наибольшая вероятность быть выбранными для дальнейшего исследования. Две фазы поискового процесса, прямой и обратный проход, чередуются NC раз, то есть до тех пор, пока каждая пчела не произведет NC модификаций своего решения. Когда все шаги завершены, определяется лучшее из B имеющихся решений (оно используется для обновления глобального лучшего решения). После этого итерация считается завершенной. Все B решений удаляются, и стартует новая итерация. Критерием останова алгоритма может выступать, например, максимальное число итераций или суммарное время работы алгоритма. Вероятность того, что b-я пчела перед началом очередного прямого прохода останется лояльной своему текущему решению (то есть не откажется от него), выражается формулой
где Ob – нормализованное значение целевой функции решения, созданного b-й пчелой; Omax – максимальное среди всех значений Ob (b = 1, 2, …, B); u – порядковый номер прямого прохода в пределах данной итерации (u = 1, 2, …, NC). Нормализованные значения целевой функции рассчитываются следующим образом. Пусть Cb – значение целевой функции для b-й пчелы, Cmax и Cmin – соответственно максимальное и минимальное значения целевой функции в пределах улья. Тогда для задачи минимизации [10]
Для каждой пчелы, отказавшейся от своего решения (их (B–R) штук), необходимо найти рекрута, то есть выбрать одно из R решений, к которым их пчелы остались лояльными. Вероятность того, что решение данного конкретного рекрута будет выбрано любой из пчел, отказавшихся от своего решения, выражается формулой
В работе [10] рассматривается концепция использования глобальной памяти в алгоритме BCO. Предлагается в конце каждой итерации не удалять все B решений, а лучшее из них делать стартовым для одной из пчел на следующей итерации. Такой подход иначе называется концепцией элитаризма. Для удобства обозначим как use_global булеву переменную, показывающую, используется ли концепция элитаризма. Окрестность решения Понятие «окрестность» является ключевым для метаэвристических алгоритмов, использующих концепцию локального поиска. Для каждой кон- кретной оптимизационной задачи оно имеет свою специфику. В случае ЗРБС решение представляет собой множество БС с подключенными к ним клиентами. Задача построения окрестности состоит в определении множества решений, являющихся в некотором роде близкими к текущему решению. Введем операцию «переподключение одного клиента» (имеется в виду подключение клиента к другой БС). Если мы ищем новую БС для i-го клиента, то мы должны последовательно, проверяя выполнение ограничений (1)–(3), пытаться подключить его к одному из мест-кандидатов (кроме его нынешнего места), начиная с самого ближнего к нему. Место w, к которому нужно подключить клиента, должно иметь активную БС (Sol[w].type ≠ 0). Предлагается формировать окрестность решения N(Sol) путем небольших изменений в текущем решении Sol. Новое решение из окрестности текущего решения можно получить при помощи двух способов (операций). 1. Смена типа одной БС на более дешевый. Данная операция (Sol[s].type = Sol[s].type – 1) возможна для каждого элемента вектора Sol, для которого справедливо Sol[s].type > 1. После смены типа БС мы должны проверить решение Sol на выполнение ограничений (1)–(3). 2. Удаление одной БС. Подобная операция возможна для каждого места-кандидата с установленной БС. Для каждого клиента удаляемой станции s мы запускаем операцию «переподключение одного клиента». Удаление s-й станции возможно, если все клиенты s-й станции можно подключить к другим БС. Очевидно, что окрестность, получаемая при помощи применения к решению Sol операций «удаление одной БС» и «смена типа одной БС на более дешевый», содержит только решения с лучшей целевой функцией, чем у Sol. Пчелиный алгоритм решения ЗРБС Представлим общую схему алгоритма BCOi для ЗРБС в виде псевдокода. 1. Введем обозначения: Best – лучшее решение задачи; cost_best – целевая функция Best. 2. Best = Æ. cost_best = ¥. 3. If (use_global ¹ true) or (Best = Æ) then For b = 1 to B Построить начальное решение Currb. End for Else Curr1 = Best For b = 2 to B Построить начальное решение Currb. End for End if 4. For s = 1 to NC For b = 1 to B // прямой проход 1) Построим N(Currb) окрестность решения Currb. 2) Wb = Æ. 3) Цикл. Для каждого решения Sol из построенной окрестности выполним: 3.1) Если решение Sol недопустимое [не удовлетворяет одному из ограничений (1)–(3)], то переход к следующей итерации цикла. 3.2) Если F(Sol) >= F(Currb), то переход к следующей итерации цикла. 3.3) Добавить Sol в множество Wb. 4) Если Wb ¹ Æ, выберем одно решение из Wb при помощи метода рулетки и присвоим его Currb. 5) Если F(Currb) < cost_best, то Best = Currb, cost_best = F(Currb). End for // обратный проход R = 0. Gnon_loyal = Æ. // множество пчел, которые отказались от своих текущих решений Gloyal = Æ. // множество пчел, которые не отказались от своих текущих решений If (s ¹ NC) then Рассчитать нормализованные значения целевой функции для каждой пчелы по формуле (6). For b = 1 to B 1) Найти 2) Пусть z – случайное число из диапазона [0; 1]. Если z > End for For b = 1 to B If (b Î Gnon_loyal) then При помощи метода рулетки присвоим пчеле b решение одной из пчел из множества Gloyal согласно формуле (7). End if End for End if End for 5. Обнулим все решения Currb (b = 1, 2, …, B). 6. Если время работы алгоритма (time) истекло, то переход к п. 7, иначе – к п. 3. 7. Вернем Best в качестве решения задачи. Компьютерное моделирование Разработанный алгоритм был реализован в среде программирования Embarcadero Delphi 2010. С помощью данного ПО проведен ряд вычислительных экспериментов по нахождению оптимального решения ЗРБС. Моделирование проводилось на компьютере со следующими параметрами: процессор Intel Core i5-3470, 6 ГБ оперативной памяти. Первая серия вычислительных экспериментов была посвящена исследованию быстродействия и точности предложенного пчелиного алгоритма BCO путем сравнения его с методом полного перебора (ПП). Принцип ПП состоит в следующем: перебрать все возможные решения задачи, отбросить недопустимые, а среди оставшихся выбрать решение с минимальным значением целевой функции. Так как метод ПП не позволяет решать задачу за полиномиальное время, сравнение проводилось на задачах малой и средней размерности. Зафиксируем параметры пчелиного алгоритма: B=5, NC=10, use_global=true. Результаты работы алгоритмов приведены в таблице 1. Каждая ячейка таблицы содержит две строки: верхняя – время работы алгоритма в секундах при решении задачи определенной размерности, нижняя – значение соответствующей целевой функции в условных единицах стоимости. Время решения задачи для метода BCOi – среднее за 10 запусков алгоритма, значение целевой функции для BCOi – лучшее за 10 запусков алгоритма. Представленные в таблице 1 данные свидетельствуют о том, что на задачах малой размерности пчелиный алгоритм обеспечивает получение точных значений целевой функции, как и метод полного перебора, дающий точное решение при каждом запуске алгоритма. При этом предложенный пчелиный алгоритм справляется с решением ЗРБС за очень малое время. Таблица 1 Сравнение пчелиного алгоритма и метода ПП Table 1 Comparison of BCOi and exhaustive search
Далее был проведен ряд вычислительных экспериментов с целью выявления влияния использования глобальной памяти (концепции элитаризма) в методе BCO на качество получаемых решений за- дач средней и большой размерности. Зафиксированные параметры пчелиного алгоритма: B=5, NC=10. Моделирование производилось следующим образом: каждая из задач решалась двумя способами (use_global=true и use_global=false), на нахождение решения отводилось одинаковое время (30 сек.), значения по итогам 100 запусков усреднялись. Результаты эксперимента приведены в таблице 2. Каждая ячейка таблицы содержит две строки: верхняя – время работы алгоритма (при данных значениях управляющих параметров) в секундах при решении задачи определенной размерности, нижняя – соответствующее значение оценки относительной погрешности решений в процентах. Относительная погрешность решений вычисляется как среднее отклонение полученных решений от лучшего из известных решений задачи. Из таблицы 2 видно, что алгоритм, подразумевающий использование элитаризма, решает ЗРБС лучше алгоритма без использования элитаризма. Таблица 2 Влияние использования глобальной памяти на решение задачи Table 2 Impact of the global memory use on problem solving
Таблица 3 Влияние числа пчел и числа проходов на решение задачи Table 3 Impact of the number of bees and the number of passes on problem solving
Также был проведен ряд вычислительных экспериментов с целью выявления влияния числа особей в рое и числа проходов в пределах одной ите- рации на качество получаемых решений задач средней и большой размерности. В качестве тестового примера была выбрана задача следующей размерности: Ntp=100, Nps=100, Ntypes=3. Зафиксированные параметры пчелиного алгоритма: use_global= =true. Результаты эксперимента приведены в таблице 3. Каждая ячейка таблицы содержит две строки: верхняя – время работы алгоритма BCOi в секундах при определенных значениях B и NC, нижняя – соответствующее значение оценки относительной погрешности решений в процентах. Как и в предыдущем эксперименте, данные для каждой пары B и NC усреднялись по результатам 100 запусков алгоритма, один запуск подразумевал 30 секунд на нахождение решения. Из таблицы 3 видно, что наилучшие результаты получаются при B=5, NC=10, что согласуется с данными, приводимыми в работе [13]. Проведенные вычислительные эксперименты позволяют сделать следующие выводы. Предложенная модификация пчелиного алгоритма BCO позволяет находить решение ЗРБС. Для задач малой и средней размерности результаты пчелиного алгоритма совпадают с результатами алгоритма полного перебора. При этом предложенный метод решает задачу на много порядков быстрее. Разработанное на основе созданного алгоритма ПО может находить решение задач средней и большой размерности за время, не превышающее 1 минуту. Рекомендуемыми параметрами пчелиного алгоритма BCO, позволяющими находить хорошее решение за приемлемое время, являются следующие: B=5, NC=10, use_global=true. Литература 1. Вишневский В.М. Теоретические основы проектирования компьютерных сетей. М.: Техносфера, 2003. 512 с. 2. Ермолаев C.Ю. Оптимальное размещение базовых станций // Telecommunication Sciences. 2010. № 1. С. 349–355. 3. St-Hilaire M., Chinnek J.W., Chamberland S., Pierre S. Efficient solution of the 3G Network planning problem. Computers & Industrial Engineering. 2012, no. 4, pp. 819–830. 4. Скаков Е.С., Малыш В.Н. Использование алгоритмов мультистарта и поиска с запретами для решения задачи размещения базовых станций // Информационно-управляющие системы. 2015. № 3. С. 99–106. 5. Архангельский А.Я. Программирование в Delphi 7. М.: Бином-Пресс, 2003. 1152 с. 6. Koskie S., Gajic Z. A nash game algorithm for SIR-based power control in 3G wireless CDMA networks. IEEE/ACM Transactions on Networking. 2005, no. 5, pp. 1017–1026. 7. Karaboga D., Basturk B. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) Algorithm. Journ. of Global Optimization. 2007, no. 3, pp. 459–471. 8. Karaboga D., Akay B. A survey: algorithms simulating bee swarm intelligence. Artificial Intelligence Review. 2009, vol. 31, pp. 61–85. 9. Bonabeau E., Dorigo M., Theraulaz G. Swarm intelligence: from natural to artificial systems. NY, Oxford Univ. Press, 1999, 320 p. 10. Davidovic T., Teodorovic D., Selmic M. Bee colony optimization, Part I: The algorithm overview. Yugoslav Journ. of Ope- rations Research. 2015, no. 1, pp. 33–56. 11. Lucic P., Teodorovic D. Computing with bees: attacking complex transportation engineering problems. Intern. Journ. on Ar- tificial Intelligence Tools. 2003, no. 3, pp. 375–394. 12. Teodorovic D., Selmic M., Davidovic T. Bee colony optimization. Part II: The application survey. Yugoslav Journ. of Operations Research. 2015, no. 2, pp. 185–219. 13. Davidovic T., Ramljak D., Selmic M., Teodorovic D. Bee colony optimization for the p-center problem. Computers & Operations Research. 2011, no. 10, pp. 1367–1376. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=4179&lang= |
Версия для печати Выпуск в формате PDF (6.81Мб) Скачать обложку в формате PDF (0.36Мб) |
| Статья опубликована в выпуске журнала № 3 за 2016 год. [ на стр. 67-73 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Вопросы создания АСУ космическими полетами беспилотных аппаратов в околоземном пространстве
- Механизм прав на основе групп пользователей в eduroam – федеративной системе управления доступом к сетевым ресурсам научно-образовательных сетей
- Программный комплекс для расчета процесса нанесения покрытия в псевдоожиженном слое
- Теоретический подход к управлению социально-техническими системами
- Комплекс программного обеспечения для оптимизации надежности однородных нейронных структур
Назад, к списку статей



 (1)
(1)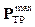 – вектор, элементами которого являются максимальные мощности клиентов;
– вектор, элементами которого являются максимальные мощности клиентов;  – вектор максимальных мощностей БС разного типа;
– вектор максимальных мощностей БС разного типа;  – вектор, элементами которого являются чувствительности клиентов;
– вектор, элементами которого являются чувствительности клиентов;  – вектор чувствительностей БС разного типа; G – двумерный массив (Ntp×Nps), каждый элемент которого 0≤G[i][s]≤1 показывает уровень затухания между s-м местом и клиентом с номером i.
– вектор чувствительностей БС разного типа; G – двумерный массив (Ntp×Nps), каждый элемент которого 0≤G[i][s]≤1 показывает уровень затухания между s-м местом и клиентом с номером i.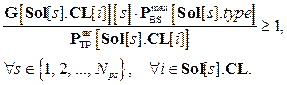 (2)
(2) (3)
(3)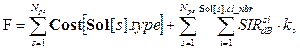 (4)
(4)
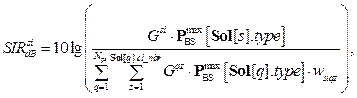
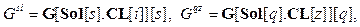
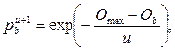 (5)
(5) (6)
(6) (7)
(7) по формуле (5).
по формуле (5). , добавим пчелу b в множество Gnon_loyal, иначе R++ и добавим пчелу b в множество Gloyal.
, добавим пчелу b в множество Gnon_loyal, иначе R++ и добавим пчелу b в множество Gloyal.