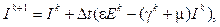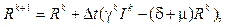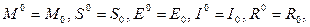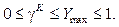Journal influence
Higher Attestation Commission (VAK) - К1 quartile
Russian Science Citation Index (RSCI)
Bookmark
Next issue
№2
Publication date:
16 June 2024
A mathematical model of computer network antivirus protection
Date of submission article: 14.06.2016
UDC: 004.942+ 518.6
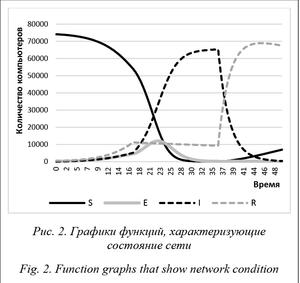
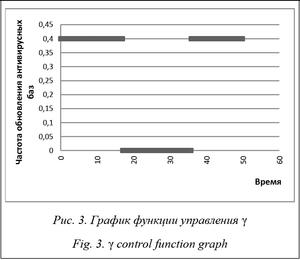
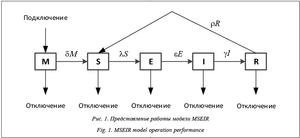
The article was published in issue no. № 4, 2016 [ pp. 125-128 ]Abstract:One of the effective approaches to analyzing computer systems in the context of active computer viruses is mathematical modeling. Its advantage is in fast modeling of various scenarios for particular parameters of a computer network. Computational results obtained by these models allow analyzing viruses’ behavior in networks consisting of any number of elements. The article considers a mathematical model of computer network protection from a malicious code based on MSEIRS model. This model is multifaceted and global as it takes into account many factors influencing a network state: timing of infection for specific viruses and network treatment using an antivirus, medium immunization rate and involuntary computer shut down. The selected control criterion characterizes the best state of the system, when most hosts are immune to the impact of network viruses. The paper presents the discrete approximation of the optimal control problem. The result of the research model is a developed program that allows you to competently evaluate the security of the network and to use effective methods of dealing with malicious code if necessary. The authors conducted and analyzed computational experiments. For this they considered two cases: a progressive virus transmission in time and network (epidemic) and the absence of significant numbers of infected computers’ fluctuations.
Аннотация:Одним из эффективных подходов к анализу процессов функционирования компьютерных систем в условиях активного распространения вредоносных программ является математическое моделирование. Его преимущество заключается в большой скорости моделирования различных сценариев для конкретных параметров компьютерной сети. Численные результаты, получаемые посредством таких моделей, позволяют анализировать поведение вирусов в сетях, состоящих из любого числа элементов. В статье рассмотрена математическая модель защиты компьютерной сети от вредоносного кода на основании модели MSEIRS. Данная модель является разносторонней и всеобщей, так как учитывает многие факторы, влияющие на состояние сети: временные параметры заражения для конкретных вирусов и лечения сети с помощью антивируса, средняя скорость иммунизации и непроизвольное отключение компьютеров от сети. Выбран критерий управления, характеризующий наилучшее состояние системы, когда большинство хостов невосприимчивы к воздействию сетевых вирусов. Построена дискретная аппроксимация исходной задачи оптимального управления. Результатом исследования модели является разработанная программа, которая позволяет грамотно оценить защищенность сети и при необходимости применить эффективные методы борьбы с вредоносным кодом. Проведены и проанализированы вычислительные эксперименты. Для этого рассмотрены два случая: прогрессирующее во времени и сети распространение вируса (эпидемия) и отсутствие существенных колебаний численности инфицированных компьютеров.
| Authors: N.A. Semykina (semykina.tversu@yandex.ru) - Tver State University (Associate Professor), Tver, Russia, Ph.D, I.V. Shavykina (inna.shavykina@mail.ru) - R&D Institute Centerprogramsystem (Software Engineer), Tver, Russia | |
| Keywords: optimal control, differential equations, nonlinear system, mseirs model, mathematical model, computer virus |
|
| Page views: 10382 |
PDF version article Full issue in PDF (16.17Mb) Download the cover in PDF (0.62Мб) |
| Permanent link: http://swsys.ru/index.php?page=article&id=4228&lang=&lang=en&like=1 |
PDF version article Full issue in PDF (16.17Mb) Download the cover in PDF (0.62Мб) |
| The article was published in issue no. № 4, 2016 [ pp. 125-128 ] |
Perhaps, you might be interested in the following articles of similar topics:
- О применении линейного программирования для повышения живучести АСУ технологическими процессами
- Программная реализация алгоритма приближенного решения задачи управления
- Параллельный программный комплекс решения неголономных задач управления
- Комплекс программ для определения параметров электрических дуг трехфазного переменного тока, горящих на горизонтальную поверхность
- Разработка численной схемы стекловаренной печи
Back to the list of articles
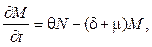 M(0) = M0,
M(0) = M0,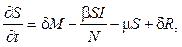 S(0) = S0,
S(0) = S0,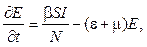 E(0) = E0, (1)
E(0) = E0, (1)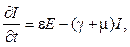 I(0) = I0,
I(0) = I0,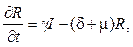 R(0) = R0.
R(0) = R0.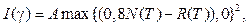 (3)
(3)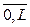 .
.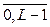 примет вид
примет вид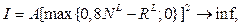


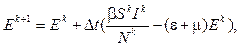 (4)
(4)