Решение ряда важных практических задач, связанных с обследованием морского дна (поиск различных аномальных зон и источников экологического загрязнения акваторий, инспекция подводных коммуникаций, поиск затонувших объектов), требует и решения задачи моделирования подводной обстановки по сенсорным данным, получаемым с помощью подводных аппаратов. Одним из наиболее приемлемых источников данных для построения 3D-моделей являются видеоизображения, из которых с помощью методов компьютерного зрения можно получать карты глубин, то есть дальностные данные, связанные с конкретным видом (проекцией) наблюдаемой сцены.
Первые работы основывались на анализе данных в 3D-пространстве сцены и в 2D-пространствах изображений видов. Подобная схема ре- шения была реализована в [1]. Данная схема не исключала дублирования треугольников при объединении множества видов. Более эффективным методом построения 3D-модели по отдельным видам является воксельный метод, впервые предложенный в работе [2]. Данный метод при высоком качестве результата демонстрировал высокую ресурсоемкость, и реконструкция даже небольшой сцены занимает много часов [3]. В работе [4] представлен обзор различных методов реконструкции поверхности по набору дальностных данных. Вок- сельный метод построения единой сеточной модели был применен в работе [5] для реконструкции и визуализации протяженных подводных сцен. Обеспечивая хорошее качество получаемой модели, он, однако, требует слишком много вычислительных ресурсов при использовании воксельного пространства с высоким разрешением. Это особенно неприемлемо в случае протяженных подводных сцен. Поэтому во многих работах усилия разработчиков были направлены на повышение алгоритмической скорости обработки данных в этом методе. Например, в работе [6] была предложена алгоритмическая база для повышения скорости обработки за счет как оптимизации вычислений, так и применения технологии CUDA. Также стоит отметить современный сурфельный подход, где для ускорения используется GPU [7] для стереореконструкции и визуализации, который при высокой скорости и качестве визуализации не дает единого сеточного представления. Использование GPU для ускорения вычислений происходит достаточно часто для решения задачи реконструкции [8], однако принципиальным подходом к ускорению вычислений в задачах обработки больших объемов пространственных данных является использование суперЭВМ с экстрамассивным параллелизмом. По- этому в данной работе применительно к задаче построения и визуализации 3D-модели подводных сцен воксельным методом предлагается подход, основанный на реализации распределенно-параллельной обработки данных на базе суперЭВМ.
Параллельная схема алгоритма
Задача формулируется следующим образом. Имеются несколько видов (ракурсов сцены), для каждого из которых на предварительном этапе была построена поверхность в виде пространственной триангуляционной сетки. Триангуляционная сетка строилась по 2D-триангуляции на регулярной пиксельной решетке изображения с использованием карты глубин. Заметим, что карта глубин вычисляется для точек, наблюдаемых на данном виде. Цель – построить единую текстурированную триангуляционную оболочку, которая и будет трехмерной триангуляционной моделью сцены.
Метод работает в воксельном пространстве сцены. Используется непрерывная неявная функция, представленная значениями в узлах воксельной решетки. Более подробное описание алгоритма построения трехмерной модели сцены по множеству ее видов можно найти в [6].
Для построения эффективной схемы распараллеливания алгоритма необходимо выявить наиболее вычислительно трудоемкие этапы его работы. В вычислительном отношении в алгоритме можно выделить следующие этапы:
- загрузка видов в оперативную память;
- определение границ сцены;
- построение индексной карты для каждого вида;
- построение скалярного поля, заданного воксельным представлением;
- построение изоповерхности по воксельному пространству.
Размер всей структуры входных данных зависит от детализации исходных видов и от их количества. Во время загрузки каждой триангуляционной сетки просматриваются координаты их вершин для построения границ всей сцены. Объединяя первый и второй этапы, можно избавиться от вторичного прохода по всем данным и тем самым повысить общую скорость работы схемы. На этапе загрузки основные затраты времени приходятся на работу внешних устройств хранения информации и использование графических ускорителей здесь неоправданно.
Предполагается, что для каждого из видов определены параметры камеры. Третий этап – построение индексной карты – выполняется для каждого вида и заключается в вычислении проекции всех треугольников сетки на экранную плоскость камеры, с которой был получен данный вид. Проекции присваивается номер соответствующего тре- угольника (индекс). Вычислительная сложность этого этапа определяется следующими параметрами:
- размер триангуляционной сетки (количество треугольников);
- размер/разрешение проекции (задается пользователем и, как правило, выбирается равным размерам исходных видов).
Размер проекции определяется степенью детализации индексной карты, что, в конечном счете, влияет на качество итоговой единой триангуляционной поверхности. Схема построения индексной карты на CUDA имеет одно узкое место. При заполнении индексной карты два треугольника со смежным ребром могут обращаться к одной и той же памяти для внесения своего индекса. В этом случае индекс, который записывается в индексную карту, определяется наименьшим расстоянием точки прообраза до камеры. Такая проверка влияет на эффективность работы алгоритма на CUDA, поскольку возникает взаимозависимость между параллельно вычисляемыми потоками. Каждый поток вычисляет одну пространственную точку фрагмента, и может возникнуть ситуация, когда сравниваются расстояния до камеры для нескольких точек из параллельных потоков. В этом случае целесообразно применять атомарные функции, которые выполняют часть операций последовательно. Тестирование показало, что и в этом случае реализация на CUDA обеспечивает преимущество в производительности в сравнении с CPU-версией.
На четвертом этапе выполняется основная часть вычислений, связанная с построением воксельной модели объекта. Вычислительная сложность на этом этапе определяется только детализацией воксельного представления. Для каждого вокселя необходимо построить проекции этого вокселя на все индексные карты и вычислить значение скалярной. При этом вычисления для каждого вокселя не зависят от других узлов воксельной решетки, и данный метод может быть эффективно реализован на CUDA.
На последнем этапе выполняется построение результирующей изоповерхности в воксельном пространстве методом марширующих кубиков [9]. Здесь была использована известная эффективная реализация на CUDA [10].
Используемый вычислительный кластер
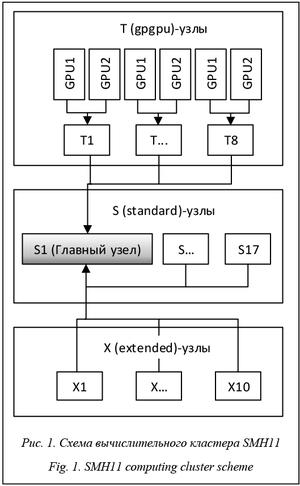 Для решения поставленной задачи использовался гибридный вычислительный кластер Института автоматики и процессов управления ДВО РАН: smh11.cc.dvo.ru. Он представляет собой вычислительную систему из нескольких групп узлов, различающихся аппаратными ресурсами (рис. 1).
Для решения поставленной задачи использовался гибридный вычислительный кластер Института автоматики и процессов управления ДВО РАН: smh11.cc.dvo.ru. Он представляет собой вычислительную систему из нескольких групп узлов, различающихся аппаратными ресурсами (рис. 1).
1. Простые узлы (17 штук) для MPI-вычислений (Standard):
- процессор: 4xCPU AMD 12-Core Opteron 6164HE;
- частота процессора: 1,7 GHz;
- кэш L1: 12 x 64 KB instruction caches + 12 x 64 KB data caches;
- кэш L2: 12 x 512 KB;
- кэш L3: 2 x 6 MB;
- FSB: 3200 MHz (Hyper Transport links);
- память: 64 Gb оперативной памяти DDR3-1333 MHz ECCReg;
- диск: SSD SATA 2.5" 96 Gb MLC Chip;
- управляющая сеть: Ethernet 1Gb;
- MPI сеть: Infiniband 4xQDR (40 Gb/s) + Ethernet 1Gb.
2. Узлы с увеличенной оперативной памятью (Extended, 10 штук):
- процессор: 4xCPU AMD 12-Core Opteron 6164HE;
- частота процессора: 1,7 GHz;
- кэш L1: 12 x 64 KB instruction caches + 12 x 64 KB data caches;
- кэш L2: 12 x 512 KB;
- кэш L3: 2 x 6 MB;
- FSB: 3200 MHz (Hyper Transport links);
- память: 128 Gb оперативной памяти DDR3-1333 MHz ECC Reg;
- диск: 4xSSD SATA 2.5" 96 Gb MLC Chip.
3. Гибридные узлы (gpgpu, 8 штук):
- процессор: 2xCPU Xeon L5506 4.8 GTsec;
- частота процессора: 2.13 GHz;
- кэш L1: 64 KB;
- кэш L2: 1024 KB;
- кэш L3: 4 MB;
- FSB: 4.8 GT/s QPI (2400 MHz);
- графический чип: 2xNVIDIA Tesla M2050 GPU computing processor – 3 GB;
- память: 32 Gb оперативной памяти DDR3-1333MHz ECC Reg;
- диск: SATA DOM 32 Gb;
- управляющая сеть: Ethernet 1Gb, MPI сеть: Infiniband 4 QDR (40 Gb/s) + Ethernet 1 Gb.
Коммуникация между узлами возможна только в рамках своей группы. В данной работе использовались узлы типа T, так как только они имеют по две NVIDIA-видеокарты на узел, соответственно, поддерживают CUDA.
Наличие нескольких узлов позволяет распределять вычислительную нагрузку между ними посредством MPI. Таким образом, используя все узлы, получим 8 CPU-узлов и 16 CUDA-устройств (по 2 на каждый узел). Отметим также, что обмен между CUDA-устройством и хостом возможен только в пределах одного узла.
Распределение вычислительной нагрузки
Эффективность параллельной вычислительной схемы – это эффективное использование имеющихся вычислительных ресурсов. Основными критериями эффективности реализации можно считать максимальное задействование всех доступных ресурсов в каждый момент времени, минимизацию простоев вычислительных узлов и задержек при передаче данных. В работе были использованы два типа параллельных архитектур: MPI (параллелизм в рамках кластера) и CUDA (параллелизм на графическом ускорителе). Только учитывая особен- ности каждой из архитектур вычислительного комплекса, можно построить эффективную схему распараллеливания предложенного алгоритма.
Преимущества MPI: высокая производительность каждого отдельно взятого потока, высокая скорость передачи данных между потоками. Главный недостаток MPI: малое количество полноценных потоков, определяемое суммарным количеством ядер во всех процессорах кластера. Преимущества CUDA: большое количество параллельно выполняемых потоков. Недостатки CUDA: сравнительно невысокая вычислительная производительность каждого отдельно взятого потока, неэффективный обмен данными между потоками, а также между хостом и устройством, ограниченный объем памяти GPU.
С учетом особенностей гибридного кластера и наличия вычислителей двух видов был обоснован выбор вида параллелизма на каждом этапе вычислительной схемы.
На этапе загрузки видов выполняются считывание с диска и загрузка данных в оперативную память. В данном случае наиболее эффективный способ ускорения процесса – распределение загрузки файлов между узлами MPI. Тогда каждый узел не будет загружать полный набор файлов.
Этап загрузки объединен с этапом поиска границ части объекта, а размер всей области может быть получен с помощью обмена локальными размерами с каждого узла с помощью MPI.
На этапах создания индексных карт, вычисления скалярной функции и построения изоповерх- ности выполняется большой объем однотипных, независимых вычислений в воксельном пространстве. Поэтому они могут быть эффективно реализованы на CUDA. Тем более что процесс создания индексных карт по сути является процессом растеризации полигональных моделей, то есть естественным для работы графического ускорителя.
Как уже упоминалось, одним из узких мест графических ускорителей является высокая стоимость операции передачи данных между хостом и устройством. Так как все три этапа реализуются на CUDA, в целях минимизации расходов передача данных происходит только дважды: из хоста на устройство копируются параметры воксельного пространства, индексные карты и полигональные модели, а из устройства на хост копируется результирующая изоповерхность.
Кластер содержит 8 узлов с 2 графическими ускорителями на каждом, что позволяет одновременно рассчитывать 16 сегментов объекта. Сегмент – это часть воксельной структуры. Например, воксельная структура размером 1024´1024´1024 разбивается на 16 сегментов размером 64´1024´ ´1024. Такой размер сегмента в оперативной памяти графического ускорителя занимает 256 Мб. Если для большей детализации выбрано разбиение по стороне более чем 212, то размер сегмента в оперативной памяти будет занимать уже более 16 Гб, что значительно больше оперативной памяти графических вычислителей. В этом случае каждый сегмент необходимо еще разбить на более мелкие фрагменты, что не изменит вычислительную схему. А так как готовый полигональный фрагмент всей сцены формируется полностью на GPU, разбиение сегментов на более мелкие фрагменты не повлечет за собой дополнительные расходы на передачу данных между CPU и GPU.
Пусть n – степень разбиения воксельной модели, тогда для хранения данных с плавающей запятой одинарной точности всей воксельной структуры необходимо 23n+2 байт. Если K – количество GPU с памятью, равной M байт, а S – память для хранения исходных данных (индексные карты и ис- ходные полигональные сетки), то количество фраг- ментов для каждого узла
 .
.
В случае, когда F>1, процесс обработки фрагментов на GPU происходит последовательно.
Применительно к используемому в данной работе гибридному кластеру для сеток с глубиной менее 11 достаточно 1 фрагмента на каждый GPU. Для n=12 уже потребуется 6 фрагментов на GPU.
Поэтапное распределение вычислительной нагрузки на гибридном кластере показано на рисунке 2.

Результаты тестирования
Для получения оценки эффективности предложенной параллельной схемы алгоритма были проведены вычислительные эксперименты на реальной сцене «Пизанская башня» (рис. 3, 4), данные для которой были получены со сканера Range Vision Premium 5 Mpix. Параметры используемого вычислительного оборудования: процессор Intel Core i5 3.3 Ггц и вычислительный кластер, описанный выше. Время работы алгоритма на разных вычислительных устройствах приведено в таблице. Как и ожидалось, наблюдается почти 70-кратное ускорение работы базового алгоритма с применением CUDA даже на одном ускорителе. Применение всех 16 графических ускорителей кластера дает еще 6-7-кратный прирост производительности. Нелинейность ускорения объясняется здесь тем, что окончательная сборка сцены происходит на одном CPU-кластере.

Результаты тестирования алгоритма на вычислительном кластере для разных разрешений воксельного пространства
The results of algorithm testing on a computing cluster for different voxel resolutions
|
Вычислитель
|
Размер сетки
|
|
5123
|
10243
|
20483
|
40963
|
|
CPU i5, 3.3 Ггц, 24 Гб ОЗУ, 4 ядра (сек.)
|
12
|
75
|
369
|
-
|
|
CUDA 1xTesla M2050 (сек.)
|
-
|
< 1
|
4,2
|
67
|
|
CUDA 16xTesla M2050 (сек.)
|
-
|
< 1
|
< 1
|
10,4
|
|
Количество треугольников (млн)
|
1,2
|
14,8
|
89,3
|
447
|
Заключение
Предложенная схема многопроцессорной об- работки на базе гибридного вычислительного кластера в задаче построения и визуализации трехмерной модели сложной сцены по дальностным данным позволила повысить вычислительную производительность более чем на два порядка. Аналогичная схема может применяться и в других задачах, связанных с обработкой больших объемов пространственных данных.
Работа выполнена при финансовой поддержке РФФИ (проект № 15-07-00341), Программ Президиума РАН (проект № 0262-2014-0157) и «Дальний Восток» (проект № 15-I-4-025).
Литература
1. Mordohai P., Frahm J.-M., Akbarzadeh A., etc. Real-time video-based reconstruction of urban. ISPRS Working Group V4 Workshop 3D-ARCH 2007: 3D Virtual Reconstruction and Visualization of Complex Architectures (ETH Zurich, Switzerland). 2007, pp. 121–131.
2. Curless B., Levoy M. A Volumetric method for building complex models from range images. Proc. Conf. Computer Graphics (SIGGRAPH '96). 1996, pp. 303–312.
3. Goesele M., Curless B., Seitz S.M. Multi-view stereo revisited. Computer Vision and Pattern Recognition, Proc. IEEE Comp. Society Conf. 2006, vol. 2, pp. 2402–2409.
4. Seitz S., Curless B., Diebel J., Scharstein D., Szeliski R. A Comparison and evaluation of multi-view stereo reconstruction algorithms. Vision and Pattern Recognition. Proc. IEEE Comp. Society Conf. 2006, vol. 1, pp. 519–526.
5. Johnson-Roberson M., Pizarro O., Williams S.B., Mahon I. Generation and visualization of large-scale three-dimensional reconstructions from underwater robotic surveys. Jour. of Field Robotics, Spec. Iss.: Three-Dimensional Mapping, 2010, vol. 27, iss. 1, part 3, pp. 21–51.
6. Бобков В.А., Кудряшов А.П. Воксельный метод построения триангуляционной поверхности по множеству видов // Информатика и системы управления. 2012. № 2. С. 31–38.
7. Ju Yong Chang, Haesol Park, In Kyu Park, etc. GPU-friendly multi-view stereo reconstruction using surfel representation and graph cuts. Comp. Vision and Image Understanding, 2011, vol. 115, iss. 5, pp. 620–634.
8. Mak J., Hess-Flores M., Recker S., etc. GPU-accelerated and efficient multi-view triangulation for scene reconstruction. Proc. IEEE Winter Conf. on Applications of Comp. Vision, Steamboat Springs, CO, 24–26 March 2014, pp. 61–68.
9. Lorensen W.E., Cline H.E. Marching cubes: A high resolution 3D surface construction algorithm. In Proc. Conf. Computer Graphics (SIGGRAPH ’87). 1987, vol. 21, pp. 163–169.
10. Dyken C., Ziegler G. PGU-accelerated data expansion for the Marching Cubes algorithm. In Proc. PGU Technology Conf., San Jose (CA), Sep. 23, 2010, pp. 115–123.




 .
.

