Задача кластеризации – одна из главных задач интеллектуального анализа данных [1–4]. Она особенно значима, когда выступает одним из этапов анализа данных, построения законченного аналитического решения. Аналитику обычно легче выделить в группу схожие объекты, изучить их особенности и построить для каждой группы отдельную модель данных. Таким приемом постоянно пользуются для обработки банков данных [5–8].
Новизна разработанных методов и подходов к решению задачи кластеризации заключается в использовании методов, инспирированных природными системами: генетическим, муравьиным и пчелиным алгоритмами. Они позволяют ускорить процесс обработки банков данных. Применение таких подходов дает преимущество в решении NP-полных, трудных задач [9–12]. Рассмотрим постановку задачи кластеризации.
Постановка задачи кластеризации
Пусть X – множество объектов, Y – множество меток кластеров и задана функция расстояния между объектами:
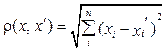 , (1)
, (1)
где xi, x¢i – характеристики объектов. Тогда существует конечная обучающая выборка объектов:
Xm={x1, …, xm}ÌX. (2)
Эту выборку необходимо разбить на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый из них состоял из объектов, близких по метрике ρ, а объекты разных кластеров существенно отличались. При этом каждому объекту xi ∈ Xm приписывается метка кластера yi.
Алгоритм кластеризации – это функция a: X →Y, которая любому объекту x ∈ X ставит в соответствие номер кластера y ∈ Y.
Множество Y в некоторых случаях известно заранее, однако чаще ставится задача определения оптимального числа кластеров с точки зрения того или иного критерия качества кластеризации. При решении задачи кластеризации метки исходных объектов yi изначально не заданы, и даже само множество Y может быть неизвестно [1–4].
В рамках данной работы банк данных имеет величину в 500 элементов, полученных случайным образом (см. таблицу).
Банк элементов
A bank of elements
|
Элемент
|
Характеристика
|
|
X
|
Y
|
Z
|
V
|
|
1
|
36
|
15
|
4
|
61
|
|
2
|
69
|
23
|
11
|
32
|
|
3
|
93
|
69
|
43
|
33
|
|
4
|
23
|
33
|
28
|
80
|
|
5
|
70
|
24
|
33
|
47
|
|
6
|
79
|
98
|
87
|
80
|
|
-
|
-
|
-
|
-
|
-
|
|
500
|
18
|
5
|
62
|
10
|
Требуется разбить его на N кластеров: G1, G2, G3, …, но при этом уже существует некоторое разбиение, которое необходимо оптимизировать, минимизировав среднее внутреннее кластерное расстояние или целевую функцию (ЦФ):
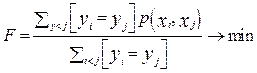 , (3)
, (3)
где xi, yi – характеристики центра кластера; xj, yj – усредненные характеристики объектов.
 В данной работе для оптимального решения задачи кластеризации производится случайное разбиение на кластеры, которое представляет собой вектор (рис. 1). Длина вектора равна количеству элементов банка данных, а также n элементов со значением 0, означающих конец одного кластера или начало другого [9–12].
В данной работе для оптимального решения задачи кластеризации производится случайное разбиение на кластеры, которое представляет собой вектор (рис. 1). Длина вектора равна количеству элементов банка данных, а также n элементов со значением 0, означающих конец одного кластера или начало другого [9–12].
Для подсчета ЦФ необходимо найти центр каждого кластера. Для этого подсчитываются усредненные значения каждой характеристики для кластера в целом:
 , (4)
, (4)
где А – значение характеристики; n – количество всех значений характеристики А.
 На рисунке 2 приведены усредненные значения характеристик для каждого кластера в целом. После нахождения центров кластеров подсчитываем ЦФ по формуле (3) и получаем ЦФ1 = 50, ЦФ2 = 43, ЦФn = 63.
На рисунке 2 приведены усредненные значения характеристик для каждого кластера в целом. После нахождения центров кластеров подсчитываем ЦФ по формуле (3) и получаем ЦФ1 = 50, ЦФ2 = 43, ЦФn = 63.
Классические последовательные алгоритмы переставляют один случайный элемент из одного кластера в другой и снова производят подсчет, что является трудоемким процессом. Действия повторяются до тех пор, пока кластеры не будут полностью заполнены, а ЦФ не станет квазиминимальной [13–15]. Рассмотрим алгоритмы, разработанные для оптимизации процесса разбиения на кластеры.
Описание алгоритмов и программного комплекса
Особенностью предложенного подхода является использование алгоритмов, моделирующих процесс живой природы. Разработанные алго- ритмы моделируют различные аспекты эволюции [9–13, 16–20].
Генетический алгоритм (ГА) моделирует процесс образования хромосом путем скрещивания, мутации и отбора [10, 12, 13, 16]. Это основная составляющая в природе. Муравьиный и пчелиный алгоритмы являются методами роевого интеллекта, главная составляющая которого – моделирование поведения живых организмов при коллективном взаимодействии [10, 17–20]. Случайное разбиение на кластеры в алгоритмах, инспирированных природными системами, формирует хромосому (набор альтернативных решений).
Основная цель ГА – минимизировать число внутрикластерных связей между элементами или максимизировать число внешних связей кластеров. При решении оптимизационных задач ГА имеет ряд преимуществ. Одно их них – адаптация к изменяющейся внешней среде. В процессе решения поставленная задача может подвергаться изменениям. Использование традиционных методов приводит к большим затратам машинного времени.
Алгоритмы роевого интеллекта (муравьиный и пчелиный) описывают поведение в многоагентных системах [10, 17–20]. Цель пчелиного алгоритма – разбить предоставленную информацию на участки. Путем исследований с помощью агентов производится поиск эффективного решения в центрах полученных участков. Если решение было найдено в окрестностях данной точки, агенты отправляются для полного и точного поиска эффективных решений.
Муравьиный алгоритм моделирует поведение муравьев в колонии. Поиск участков пищи производится сообща группой агентов. Проходя некоторый путь, агент помечает его феромоном – отличительное свойство агентов не возвращаться в точку, в которой уже были. Путем накопления феромона после прохождения всей группы происходит формирование кластера, и решения, попавшие в замкнутый участок, являются эффективными.
Для реализации задачи кластеризации был создан программный комплекс, к основным параметрам которого относятся количество элементов и настройки разработанных алгоритмов. Размеры кластеров генерируются случайно. После того, как кластеры созданы (или загружены из файла), необходимо произвести настройку разработанных алгоритмов.
Генетический алгоритм
Для эффективного использования ГА необходимо определить метод генерации начальной популяции. Существует множество методов построения начальной популяции [10, 12, 13]. В данной работе используется решето Эратосфена. Это алгоритм нахождения всех простых чисел до неко- торого целого числа n. Решето подразумевает фильтрацию всех чисел, за исключением простых. По мере прохождения списка нужные числа остаются, а ненужные (они называются составными) исключаются. Рассмотрим модифицированные генетические операторы, используемые для решения задачи кластеризации.
Оператор кроссинговера. Процесс, при котором происходят сближение двух гомологичных хромосом при созревании половых клеток и обмен частями. Существуют различные модификации оператора кроссинговера. Из-за большой информационной нагрузки в данной работе используется упорядоченный оператор кроссинговера, при котором у родителей выбирается точка разрезания, относительно которой будет происходить копирование элементов. Выбираются элементы из левого сегмента первого родителя и копируются в первого ребенка, а остальные позиции копируются из второго родителя в упорядоченном виде слева направо, но исключаются элементы, уже попавшие в первого ребенка [10].
Операторы вставки и удаления. Данные операторы являются модификацией оператора мутации.
Оператор удаления позволяет удалять строительные блоки из родительских хромосом, тем самым создавая хромосому потомка.
Оператор вставки позволяет вставлять строительные блоки в родительскую хромосому для создания потомка.
Данные операторы эффективны для использования в ГА. Применяя оператор удаления, случайный ген со значением 0 удаляется из разбиения, тем самым расширяет некоторый кластер. Дальше происходит выполнение оператора вставки, который случайным образом выбирает точку разреза. На месте точки разреза оператор фиксирует разбиение хромосомы геном со значением 0, образуя новые кластеры. Эффективность данных операторов показывает их умение быстро анализировать текущую популяцию альтернативных решений [10].
Оператор селекции. Это процесс, посредством которого хромосомы (альтернативные решения), имеющие более высокое значение ЦФ (с лучшими признаками), получают большую возможность для воспроизводства (репродукции) потомков, чем худшие хромосомы. Элементы, выбранные для репродукции, обмениваются генетическим материалом, создавая аналогичных или различных потомков. Различают элитную, один ко многим, многие к одним, лучшие с худшими, на основе методов ветвей и границ и т.д. селекции [10]. В данной работе рассматривается селекция лучшие с худшими. При кластеризации есть остаточный эффект от неправильного попадания в кластеры. Данный оператор позволяет стабилизировать состояние кластеров.
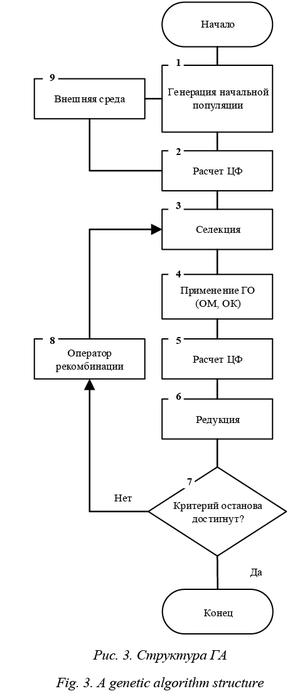 Основные этапы ГА (рис. 3).
Основные этапы ГА (рис. 3).
1. Случайным образом генерируется начальная популяция. На построение популяции оказывает влияние внешняя среда в виде ЛПР. Формиру- ется таблица характеристик для каждого гена в хромосоме.
2. Для каждой хромосомы из популяции вычисляется значение ЦФ.
3. Выполняется элитная селекция – для применения оператора кроссинговера выбираются лучшие решения.
4. Применяются генетические операторы (ГО). Первым выполняется оператор кроссинговера (ОК) – получаем потомство для последующего применения оператора мутации (ОМ).
5. К выбранным хромосомам применяется оператор мутации. При этом мутация хромосомы выполняется с некоторой вероятностью мутации, а точки мутации выбираются случайным образом.
6. Вычисляется значение ЦФ для полученных после применения оператора мутации хромосом. Таким образом, после реализации оператора мутации получается новое подмножество решений. Оно объединяется с первоначальным подмножеством решений.
7. Выполняется элитная редукция, то есть лучшие решения отбираются в следующую популяцию, а плохие удаляются. Таким образом, размер популяции остается постоянным.
8. Проверяется, достигнут ли критерий останова. В данной работе рассматривается критерий останова по времени работы алгоритма.
9. Если данный критерий не достигнут, процесс повторяется итерационно. Он выполняется на основе блока рекомбинации, который анализирует текущую популяцию альтернативных решений и управляет процессом поиска. Иначе выводятся полученные квазиоптимальные решения.
10. Конец работы алгоритма.
Пчелиный алгоритм
Оптимизационный алгоритм, моделирующий поведение пчел в живой природе, называется пчелиным алгоритмом [12, 13, 19, 20].
На начальном этапе случайным образом отправляются агенты, пытающиеся отыскать участки, где есть квазиоптимальное решение. После возвращения агенты особым образом сообщают остальным, где и сколько решений они нашли. Далее в окрестности найденных решений отправляются другие агенты, при этом, чем больше найденных решений, тем больше агентов направляются в данную окрестность. Это означает, что количество агентов в каждом направлении пропорционально значению ЦФ. Агенты продолжают искать другие квазиоптимальные решения, и процесс повторяется. Агенты живут не в двухмерной плоскости, где, зная две координаты, можно определить количество решений, а в многомерном пространстве, где один параметр функции представляется каждой координатой, которую необходимо оптимизировать. Найденное квазиоптимальное решение представляет собой значение ЦФ в этой точке.
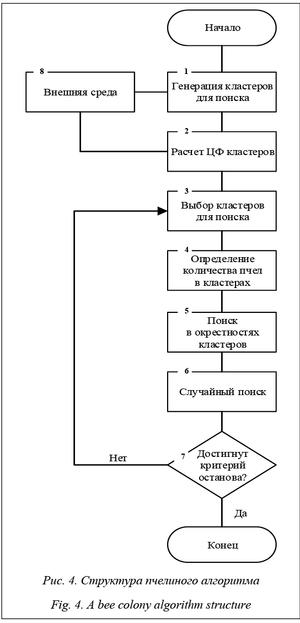 Основные этапы работы пчелиного алгоритма (рис. 4).
Основные этапы работы пчелиного алгоритма (рис. 4).
1. Генерируется начальное разбиение на кластеры для поиска. Внешняя среда оказывает влияние на построение кластеров для поиска.
2. Определяется значение ЦФ для каждого кластера.
3. Выбираются начальные кластеры, на которых будет осуществляться поиск.
4. Назначается количество агентов для поиска в окрестностях кластера. При этом количество агентов обратно пропорционально значению ЦФ. То есть, чем лучше участок, тем больше пчел для поиска, чем хуже – тем меньше пчел.
5. Производится поиск на каждом кластере. Если на кластере найдено лучшее решение, оно становится кластером для поиска.
6. Выполняется случайный поиск путем гене- рации новых решений.
7. Проверяется критерий останова: если достигнуто заданное время работы алгоритма, выводится квазиоптимальное решение, иначе продолжается поиск в окрестностях п. 5.
8. Конец работы алгоритма.
В пчелином алгоритме, как и в генетическом, решение представлено в виде закодированного вектора. Расположение источника нектара определяется этим решением, то есть решение является координатами источника. Количество нектара определяется значением ЦФ. Так как для задачи кластеризации надо минимизировать значение ЦФ, количество нектара обратно пропорционально ЦФ. Кластер имеет начальный размер, фиксируемый параметром α.
К основным настройкам относятся количество агентов, количество источников нектара (случайно количество кластеров), размер кластеров для поиска и время работы как критерий останова.
Муравьиный алгоритм
Метод роевого интеллекта описывает совместное поведение перераспределения самоформируемой системы, которая состоит из множества агентов, естественно взаимодействующих между собой и с внешней средой. Агенты просты, но, непосредственно взаимодействуя, вместе создают так называемый роевой интеллект [12, 13, 17–20].
Идея муравьиного алгоритма заключается в моделировании поведения агентов и связана с их способностью быстро находить кратчайший путь и адаптироваться к изменяющимся условиям внешней среды, находя новый кратчайший путь. При своем движении агенты помечают путь, и эта информация используется другими агентами для выбора пути. Такое элементарное правило поведе- ния и определяет способность агентов находить новый путь, если старый оказывается недоступным [3, 12, 19].
При решении оптимизационных задач необходимо разрабатывать или модифицировать нестандартные методы решения. Агенты движутся в пространстве по случайному маршруту. Маршрут разбивается на равнозначные участки. Передвижение агентов фиксируется весовым коэффициентом, который увеличивается от прохождения агента по участку маршрута. Дальше необходимо выбрать эвристику строительства решения и, если эффективное решение не найдено, реализовать оптимальный локальный поиск.
Для определения начального расположения агентов используется стратегия «Дробовик» – случайное распределение агентов в центрах кластеров, причем необязательно, чтобы численности агентов и центров совпадали.
Любой агент получает информацию о весовом коэффициенте, повышающем вероятность прохождения агента по данному участку маршрута. Весовой коэффициент в момент времени t на участке Dij будет соответствовать τij(t). Начальное значение коэффициента задается как некоторое ненулевое натуральное число (0 ≤ τij(t) ≤ 1). Если участок маршрута не проходят некоторое время t, то весовой коэффициент изменяется по формуле
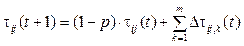 , (5)
, (5)
где m – количество агентов; p – коэффициент изменения (0 ≤ p ≤ 1).
Задача кластеризации – минимизировать среднюю сумму внутреннего кластерного расстояния:
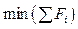 , (6)
, (6)
где Fi – длина вектора, попавшего в замкнутый участок.
 Рассмотрим предложенный авторами алгоритм (рис. 5).
Рассмотрим предложенный авторами алгоритм (рис. 5).
1. Ввод исходных данных – генерация элементов банка данных, ввод количества элементов.
2. Ввод параметров – ввод времени работы ал- горитма и количества агентов.
3. Начальное размещение агентов – случайное распределение агентов в центрах кластеров (производится с использованием стратегии «Дробовик»).
4. Осуществление итераций, количество которых определяется пользователем в п. 2.
5. Перемещение агентов – каждый агент посещает каждый элемент по одному разу.
6. Присвоение весового коэффициента участку маршрута: начальное значение весового коэффициента задается как некоторое ненулевое натурально число (0 ≤ τij(t) ≤ 1).
7. Изменение весового коэффициента по формуле (5).
8. Поиск лучшего текущего решения на основании формулы (6).
Серия вычислительных экспериментов показала, что эффективность муравьиного алгоритма возрастает с увеличением размера оптимизационных задач. Важной особенностью муравьиного алгоритма является конвергенция альтернативных решений. После большого числа итераций при одновременном использовании большого количества решений нет больших задержек в локальных экстремумах. К настройкам муравьиного алгоритма относят количество агентов, весовые коэффици- енты α, β, формирующие представление о приоритете выбранного участка маршрута. Коэффициент изменения показывает степень снижения приоритетности выбранного участка маршрута.
Разработка программного комплекса
Для эффективного решения задач интеллектуального анализа данных, в частности задачи кластеризации, предлагаются эвристические алгоритмы, преобразующие одно конечное множество альтернативных решений в другое, используя для этого механизмы и принципы генетики и эволюции живой природы [5, 9–13, 16].
На рисунке 6 представлена укрупненная архитектура модели биоинспирированного поиска, разработанная в процессе написания программного комплекса. Данная модель анализирует поведение ЦФ при использовании трех различных эвристических алгоритмов. Использование модели дает возможность решать задачи кластеризации с любыми наборами исходных данных.
1. На входе генерируется начальная популяция альтернативных решений под воздействием внешней среды (ЛПР).
2. Выбирается алгоритм кластеризации элементов (генетический алгоритм – ГА, муравьиный алгоритм – МА; пчелиный алгоритм – ПА). На основе выполнения алгоритмов строится популяция альтернативных решений.
3. Применив отбор, ЛПР получает набор квазиоптимальных решений кластеризации.
4. Если квазиоптимальное решение не удовле- творяет, повторяем шаг 2.
5. Иначе на выходе получаются набор квазиоптимальных решений и функция времени, которая показывает эффективность представленной модели.
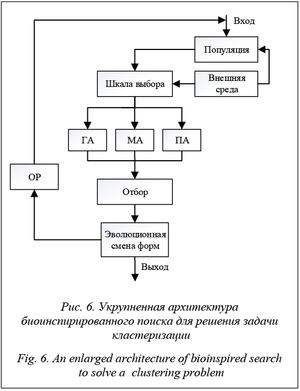
Основная идея данной модели – моделирование распараллеливания процесса обработки больших объемов данных с помощью эвристических алгоритмов.
Вычислительный эксперимент
Разработанные алгоритмы относятся к классу эвристических алгоритмов. Для оценки их эффективности, а именно временной сложности, производится анализ статистических данных, которые получаются при неоднократном выполнении данных алгоритмов [21–23].
Для проведения вычислительного эксперимента кластеризации были выбраны БД со 100, 200, 300, 400, 500 элементами. Перед началом эксперимента проводится настройка алгоритмов. Приведем пользовательские настройки алгоритмов.
Генетический алгоритм:
оператор кроссинговера..... упорядочивающийся
отбор........................................ элитный
оператор селекции................ равновероятный
вероятность оператора кроссинговера....................... 10
вероятность оператора мутации................................... 90
размер популяции................. 200
время работы......................... 10 с.
Муравьиный алгоритм:
количество агентов................................. 100
вес следа феромона α............................. 1
вес следа феромона β............................. 3
коэффициент изменения......................... 0.5
время работы............................................ 10 с.
Муравьиный алгоритм имеет ряд специфических настроек. Определяется, сколько агентов будут участвовать в поиске квазиоптимальных решений. Весовые коэффициенты α и β – параметры, влияющие на приоритет выбора того или иного участка маршрута. Параметр α контролирует выбор на текущем шаге i, j. Параметр β контролирует выбор на участке i, j с оптимальным значением весового коэффициента. Коэффициент изменения определяет время, с которым происходит изменение весового коэффициента на предыдущем участке.
Пчелиный алгоритм:
количество агентов a.............................. 100
количество центров кластеров............. 20
количество агентов b.............................. 20
размер кластеров..................................... 4
время работы............................................ 10 с.
Для работы пчелиного алгоритма необходимо определиться с минимальным набором исходных данных. Количество агентов А – агентов, которые отправляются в центры кластеров для поиска эффективных решений. Если решение найдено, в него отправляются агенты для поиска других квазиоптимальных решений в окрестностях найденных решений. Количество решений является начальным назначением для агентов А. Размер кластеров измеряется в условных единицах.
Для исследования результатов эффективности в программном комплексе реализован блок вывода графика результатов выполнения, а в главном окне программы выводится квазиоптимальное значение ЦФ.
Пока не достигнут критерий останова алгоритмов на равнозначных временных участках на основании (3) минимизируется среднее внутреннее кластерное расстояние. Ось абсцисс отображает временные участки, а ось ординат – значение ЦФ на каждом участке.
Первая серия тестов: 100 элементов банка данных (рис. 7).
Значение лучших ЦФ: 1) ГА – 618, 2) МА – 583, 3) ПА – 123.
В рамках данной работы ЦФ измеряется в условных единицах для обозначения расстояния между кластерами. Из графика видно, что пчелиный алгоритм привел к наилучшему результату ЦФ за 9,36 сек. Это значение является оптимальным в рамках данной работы. Муравьиный алгоритм быстро попал в локальный оптимум. ГА показал высокую точность в поиске квазиоптимального разбиения на кластеры, даже уступая другим алгоритмам по времени поиска.
Вторая серия тестов в 200 элементов показала преимущество ГА и муравьиного алгоритма в решении поставленной задачи.
Третья серия тестов в 300 элементов показала, что пчелиный алгоритм самый быстрый и точный.
Для точности вычислительных экспериментов опустим 4-ю серию тестов на 400 элементов. Проведем пятую, заключительную, серию для анализа полученных данных.
Пятая серия тестов: 500 элементов (рис. 8).

Рассмотрим вычислительный эксперимент подробно. Из графиков видно, что пчелиный и муравьиный алгоритмы практически не уступают друг другу. ГА в начале своей работы развивает хорошую скорость, но попадает в локальный оптимум на задачах с большим набором исходных данных. Данные эксперименты подтверждают способность пчелиного и муравьиного алгоритмов находить квазиоптимальное решение на задачах с большим набором исходных данных [17–20].
Таким образом, проведя пять серий экспериментов, можно сделать вывод о преимуществах каждого из алгоритмов. Использование данных ал- горитмов кластеризации в задачах интеллектуаль- ного анализа данных зависит от поставленной задачи и исходных данных. Диаграмма на рисунке 9 показывает зависимость ЦФ от количества элементов при кластеризации.
Из диаграммы видно, насколько эффективен тот или иной алгоритм. Время выполнения каждого из алгоритмов ≈ 10 000 мс. Эффективность ГА на большом наборе данных ниже, чем у пчелиного и муравиного алгоритмов, но дает разбиение на кластеры, приближенное к оптимальному. Пчелиный алгоритм имеет ярко выраженное преимущество, что позволяет говорить о более точном разбиении. Муравьиный алгоритм показал не намного хуже пчелиного результат – на 7,5 сек.
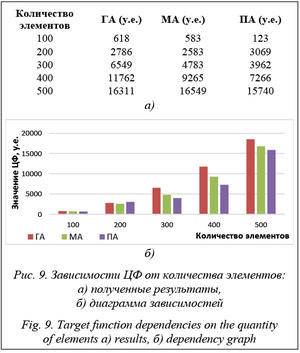 В результате выполнения алгоритмов получено эффективное формирование кластеров с наименьшими ЦФ (рис. 9). Эффективость разработанных методов исследована на основе проведения серии экспериментальных вычислений.
В результате выполнения алгоритмов получено эффективное формирование кластеров с наименьшими ЦФ (рис. 9). Эффективость разработанных методов исследована на основе проведения серии экспериментальных вычислений.
Заключение
Разработанные алгоритмы имеют ряд преимуществ. Скорость и качество работы благоприятно сказываются на дальнейшем использовании данных алгоритмов для решения задачи кластеризации. Проведенный вычислительный эксперимент показал хорошие результаты каждого из алгоритмов. В ходе серии вычислительных экспериментов время выполнения кластеризации элементов отличалось в среднем на 3–5 % от оптимального. Под оптимальным временем поиска эффективного решения в рамках данной работы понимается значение в промежутке 8–9 секунд, полученное в результате выполнения уже разработанных алгоритмов кластеризации, например k-средних. Временная сложность разработанных алгоритмов в составе программного комплекса приблизительно равна О(n2).
Особенность данного программного комплекса – в разработанных модифицированных алгоритмах. Основной модификацией ГА является применение решета Эратосфена для начальной генерации набора альтернативных решений. Совместное применение операторов удаления и вставки дает большое преимущество в поиске квазиоптимальных решений. Модификация пчелиного и муравьиного алгоритмов заключается в модификации математического представления стандартных алгоритмов.
С учетом увеличения объемов банков данных скорость обработки уменьшается прямо пропорционально количеству элементов, что приводит к труднорешаемым проблемам. Методы и подходы эволюционного моделирования являются эффективным способом решения NP-полных, трудных задач, а модификация и разработка таких мето- дов – актуальным направлением в интеллектуальном анализе данных.
Объединение алгоритмов позволяет улучшить качество работы программного комплекса и тем самым ускорить процесс поиска квазиоптимальных решений.
Работа выполнена при поддержке РФФИ, грант № 15-07-05523.
Литература
1. Чубукова И.А. Data Mining. М.: ИНТУИТ–БИНОМ. Лаборатория знаний, 2006. 382 с.
2. Котов А., Красильников Н. Кластеризация данных. 2006. URL: http://www.myshared.ru/slide/177655 (дата обращения: 28.10.2016).
3. Jain A., Murty M., Flynn P. Data clustering: a review. ACM Computing Surveys, 1999, vol. 31, no. 3, pp. 264–323.
4. Информационно-аналитический ресурс, посвященный машинному обучению, распознаванию образов и интеллектуальному анализу данных. 2008. URL: http://www.machinelearning.ru (дата обращения: 28.10.2016).
5. Воронцов К.В. Алгоритмы кластеризации и многомерного шкалирования. М.: Изд-во МГУ, 2007. 14 c.
6. Witten I.H., Eibe F., Hall M.A. Data Mining: practical machine learning tools and techniques. 3rd ed. US. Elsevier Inc, 2011, 664 p.
7. Башмаков А.И., Башмаков И.А. Интеллектуальные информационные технологии. М.: Изд-во МГТУ им. Н.Э. Баумана, 2005. 304 с.
8. Курейчик В.М., Полковникова H.A. Об интеллектуальном анализе баз данных для экспертной системы // Информатика, вычислительная техника и инженерное образование. 2013. Вып. 2. С. 39–50.
9. Курейчик В.В., Родзин С.И. О правилах представления решений в эволюционных алгоритмах // Изв. ЮФУ (Технич. науки). 2010. Вып. 7. С. 13–21.
10. Гладков Л.А., Курейчик В.В., Курейчик В.М. Генетические алгоритмы. М.: Физматлит, 2010. 306 с.
11. Курейчик В.М. Биоинспирированный поиск с использованием сценарного подхода // Изв. ЮФУ (Технич. науки). 2010. Вып. 7. С. 7–13.
12. Григораш А.С., Курейчик В.М., Курейчик В.В. [и др.]. Биоинспирированный подход к решению задач интеллектуального анализа данных. Таганрог: Изд-во ЮФУ, 2015. 100 с.
13. Кажаров А.А., Курейчик В.М. Биоинспированные алгоритмы. Решение оптимизационных задач. Germany: LAP Lamberrt Acad. Publ., 2011. 73 p.
14. Кравченко Ю.А., Запорожец Д.Ю., Лежебоков А.А. Способы интеллектуального анализа данных в сложных системах // Изв. КБНЦ РАН. 2012. Вып. 3. С. 52–57.
15. Tso B., Mather P.M. Classification methods for remotely sensed data. US, CRC Press, 2009, 349 p.
16. Курейчик В.В., Курейчик В.М. Генетический алгоритма определения пути коммивояжера // Изв. РАН (Теория и системы управления). 2006. Вып. 1. С. 94–100.
17. Редько В.Г. Моделирование когнитивной эволюции. На пути к теории эволюционного происхождения мышления. М.: Изд-во ЛЕНАНД, 2015. 256 с.
18. Сегаран Т. Программируемый коллективный разум; [пер. с англ.]. СПб: Символ-Плюс, 2015. 368 с.
19. Курейчик В.М., Кажаров А.А. Использование роевого интеллекта в решении NP-трудных задач // Изв. ЮФУ (Технические науки). 2011. Вып. 7. С. 30–36.
20. Karaboga D. An idea based on honey bee swarm for numerical optimization. Technical Report TR06, Erciyes Univ. Publ., 2005, 10 p.
21. Cormen T.H., Leiserson C.E., Rivest R.L., Stin C. Introduction to Algoritms. USA, MIT Publ., 2009 1296 p.
22. Мандель И.Д. Кластерный анализ. М.: Финансы и статистика, 1988. 342 с.
23. Айвазян С.А., Бухштабер В.М., Енюков И.С., Мешалкин Л.Д. Прикладная статистика: классификация и снижение размерности. М.: Финансы и статистика, 1989. 607 с.



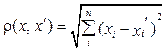 , (1)
, (1)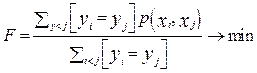 , (3)
, (3)
 , (4)
, (4)


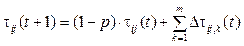 , (5)
, (5)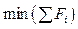 , (6)
, (6)



