Авторитетность издания
ВАК - К1
RSCI, ядро РИНЦ
Добавить в закладки
Следующий номер на сайте
№2
Ожидается:
16 Июня 2024
Идентификация состояния сложной технической системы в условиях неопределенности измерительной информации
Identification of a complex technical system functional state under conditions of measurement data ambiguity
Дата подачи статьи: 13.04.2017
УДК: 004.8
Статья опубликована в выпуске журнала № 3 за 2017 год. [ на стр. 373-377 ]Аннотация:В статье обозначена актуальная задача идентификации функционального состояния сложной технической системы в условиях повышенной зашумленности с помощью перехода к другому пространству признаков наблюдаемого состояния, определено понятие «функциональное состояние». Задача оценки функционального состояния показана как дуальная задача идентификации и распознавания образов. Уделено внимание возможному выбору параметров математических моделей, а также их структур в качестве новых признаков наблюдаемого состояния. Для решения задачи параметрической идентификации выбран метод наименьших квадратов, показывающий смену функционального состояния. В задачах контроля и испытания сложными техническими системами немаловажную роль играет процесс анализа измерительной информации. Только пройдя все этапы обработки, можно принять решение о том или ином состоянии объекта испытаний. Однако сделать это сложно в случае поступления информации очень низкого качества. Устранение данной проблемы сводится в основном к поиску решений по формированию и совершенствованию соответствующих правил принятия управленческих решений. При этом в штатных условиях и ситуациях создание таких правил во многих случаях не вызывает особых проблем, однако в нештатных условиях сделать это проблематично. Анализ состояния сложных технических объектов или их подсистем по результатам измерений предполагает решение задач структурной и параметрической идентификации. Управление сложными техническими объектами и их испытание характеризуются неопределенностью воздействия внешних факторов, аномальными и случайными погрешностями измерений. Для обеспечения требуемого качества анализа состояния их подсистем необходимо формирование принципов адаптивного управления процессом идентификации, методик оптимального выбора структуры моделей исходя из качества данных измерений. Особенно это актуально при автоматизации вторичной обработки на объектах с терминальным управлением.
Abstract:The article considers a topical problem of identification of a complex technical system functional state in conditions of increased noisiness using a transition to another attribute space of the observed state. The authors define the term “functional state”. The paper shows the problem of estimating a functional state as a dual problem of identification and pattern recognition. It pays attention to a possible selection of parameters of mathematical models and their structures as new signs of the observed state. As an example, in order to solve the parametric identification problem, the authors have selected the method of least squares. It shows the changing of the functional state. The process of analyzing measuring information plays an important role in the tasks of monitoring and testing by complex technical systems. Only after passing through all stages of processing, it is possible to decide on the condition of the test object. However, it is difficult to do in case of poor quality information. Elimination of this problem is mainly comes to searching solutions in order to form and improve relevant rules for management decision-making. At the same time, in normal conditions and situations, creation of such rules in many cases does not cause any special problems. Nevertheless, in abnormal conditions it is problematic. The state analysis of complex technical objects or their subsystems according to the measurement results assumes the solution of structural and parametric identification problems. Management of complex technical objects and their testing is characterized by uncertainty of external influence, anomalous and accidental measurement errors. To ensure the required quality of their subsystems state analysis, it is necessary to form the principles of identification process adaptive control, the methods of an optimal choice of a model structure based on the quality of measurement data. This is particularly topical for automation of secondary processing at terminal control facilities.
| Авторы: Генов А.А. (vlad_osipovv@mail.ru) - НИИСИ РАН (профессор, ведущий научный сотрудник), г. Москва, Россия, доктор технических наук, Русаков К.Д. (rusakov.msk@yandex.ru) - Институт проблем управления им. В.А. Трапезникова РАН (младший научный сотрудник), Москва, Россия, Хиль С.Ш. (skhill@mail.ru ) - Московский авиационный институт (национальный исследовательский университет) (доцент), Москва, Россия, кандидат технических наук | |
| Ключевые слова: метод наименьших квадратов, параметрическая идентификация, распознавание образов, повышенная зашумленность, сложная техническая система, функциональное состояние, идентификация состояния |
|
| Keywords: method of least squares, parameter identification, pattern recognition, increased noisiness, complex technical system, functional state, state identification |
|
| Количество просмотров: 8111 |
Статья в формате PDF Выпуск в формате PDF (21.91Мб) Скачать обложку в формате PDF (0.59Мб) |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=4304 |
Статья в формате PDF Выпуск в формате PDF (21.91Мб) Скачать обложку в формате PDF (0.59Мб) |
| Статья опубликована в выпуске журнала № 3 за 2017 год. [ на стр. 373-377 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Программное обеспечение для автоматизированного обнаружения и оценки разрушений соединительных швов зданий
- Выделение и анализ скелетов объектов на цветных снимках
- Методический подход к моделированию обеспечения сложных технических систем запасными частями
- Система автоматического картографирования знаков дорожного движения
- Современные подходы к обучению интеллектуальных агентов в среде Atari
Назад, к списку статей



 = fg(g, t, F, u), где g – вектор состояния динамической системы gT = [g1 g2 … gn], gi – параметры вектора состояния; u – вектор внешних воздействий динамической системы uT = [u1 u2 … un]; F – множество функциональных состояний динамической системы Fi Î F, Fi = f(t, П, v), где П – правило принятия решения об изменении функциональных состояний, которое выглядит следующим образом:
= fg(g, t, F, u), где g – вектор состояния динамической системы gT = [g1 g2 … gn], gi – параметры вектора состояния; u – вектор внешних воздействий динамической системы uT = [u1 u2 … un]; F – множество функциональных состояний динамической системы Fi Î F, Fi = f(t, П, v), где П – правило принятия решения об изменении функциональных состояний, которое выглядит следующим образом: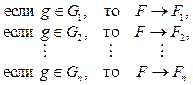


 .
. .
. .
.