В Самарском национальном исследовательском университете продолжаются разработка и реали- зация проблемно-ориентированной среды, пред- назначенной для имитационного моделирования процессов распространения и взаимодействия инфицирующих сущностей. Инфицирующими считаются сущности, экземпляры которых могут обладать неким свойством инфицированности и способны передавать это свойство другим экземплярам, не теряя его в результате передачи. Фактически речь идет не о передаче свойства, а о копировании его из одного экземпляра в другой.
Примерами процессов и явлений реального мира, для которых характерно подобное поведение, являются развитие эпидемий болезнетворных микроорганизмов среди живых существ, распространение компьютерных вирусов и червей от компьютера к компьютеру, расширение лесных пожаров, передача информационных сообщений в технических и социальных сетях и т.п. Актуальность исследования подобных процессов и явлений средствами моделирования не вызывает сомнений.
Обзор предпосылок
Традиционно для моделирования сложных процессов и явлений используются три основных под- хода: натурный, аналитический и имитационный.
Очевидно, максимальной адекватностью и информативностью обладают натурные модели, которые, однако, весьма затратны и далеко не всегда реализуемы на практике. Например, для натурного моделирования распространения компьютерных вирусов и червей требуется специально сформированная тестовая сеть, состоящая из большого количества компьютеров [1].
Аналитические модели инфицирования восходят к прототипам, разрабатываемым с XIX века для изучения эпидемий и эпизоотий среди людей и животных. В общем случае они описываются системами дифференциальных уравнений вида
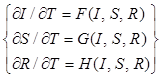 ,
,
где T – время; I – количество инфицированных, S – количество здоровых, R – количество вылеченных узлов; F, G и H – некоторые функции. Наиболее простые модели (например, с уравнениями Мальтуса и Фергюльста) решаются аналитически, однако уже модели типа Кермака–МакКендрика, не говоря о более сложных, только численно. Для достижения приемлемой адекватности приходится чрезмерно усложнять модели: например, в [2] упо- минаются аналитические модели биологических инфекций, включающие более тысячи дифферен- циальных уравнений. Чаще всего объектом изучения на аналитических моделях является асимптотическое поведение системы инфицирующих сущностей, то есть на интервале времени, стремящемся к бесконечности, и в изотропной среде. При этом игнорируются, например, анизотропность среды, непостоянство условий во времени и т.п.
Таким образом, максимальной гибкостью и информативностью при приемлемом уровне материальных затрат обладают имитационные модели. Первые опыты по имитационному моделированию инфекций (и близких к ним процессов типа динамики популяций в игре «Жизнь» Конвея или распространения перколяционной волны в пористых средах) проводились в 1960–70-х годах и представляли собой простые реализации методов Монте-Карло, предусматривающие размножение и удаление абстрактных фишек, расположенных в узлах решеток. Подобные подходы использовались на протяжении нескольких десятилетий вплоть до последнего времени, например, в работах [3–7]. Однако для увеличения адекватности имитационных моделей необходим учет большого количества разнородных и взаимодействующих друг с другом факторов, влияющих на протекание изучаемых процессов, что достижимо лишь при мультиагентном подходе. В этом случае вместо абстрактных фишек и решеток используются сколь угодно сложные и адекватные алгоритмические модели как отдельных экземпляров сущностей, так и среды их обитания. Разумеется, существуют универсальные инструментальные системы, предназначенные для мультиагентного моделирования любых процессов и явлений (например AnyLogic [8]), но они в силу своей невысокой проблемной ориентированности требуют слишком большого участия исследователя в описании и настройке проблемно-специфичных аспектов. Также имеются системы для мультиагентного моделирования именно инфекций, но они подчас решают лишь узкие классы задач, например, только в области защиты информации [4, 6] или биологии и медицины [3]. Этими обстоятельствами и обусловлена актуальность проблемно-ориентированной среды, предназначенной для мультиагентного моделирования процессов распространения и взаимодействия инфицирующих сущностей.
Основными составляющими моделей, создаваемых средствами моделирующей среды, являются модель вселенной, в которой развиваются процессы и явления инфицирования, и агентные модели экземпляров сущностей.
Модель вселенной
Пусть вселенная W = (W1ÈW2È…) – совокупность некоторого количества пересекающихся миров Wi, каждый из которых представим в виде Wi = = <, >, где Gi = (Vi, Xi) – подграф, задающий население и геометрию i-го мира; Qi = (Ai, Mi) – свод законов природы, характерных для i-го мира; Vi = {vi1, vi2,…} – множество сущностей, населяющих мир; Xi = {xi1, xi2, …} – множество отношений типа «возможно инфицирование» между сущностями; Ai = {ai1, ai2, …Ii} – множество атрибутов, которыми обладают сущности i-го мира; Mi = {mi1, mi2, …} – множество методов поведения, характерных для сущностей i-го мира.
Во множестве атрибутов сущностей i-го мира выделим логический атрибут Ii, способный принимать значения «истина» или «ложь». Передача (точнее, копирование) значения этого атрибута от одной сущности мира к другой и соответствует операции инфицирования i-м типом инфекции. При этом понятие «инфекция» имеет широкий смысл. Например, почти в любом варианте вселенной должен существовать некий j-й мир, населенный здоровыми (Ij = 0) и/или исцеляющими (Ij = 1) сущностями.
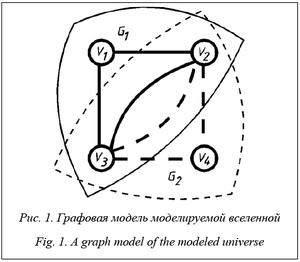 Очевидно, топология вселенной W представляет собой ориентированный мультиграф (рис. 1) в виде объединения некоторого количества односвязных подграфов G = (G1ÈG2È...).
Очевидно, топология вселенной W представляет собой ориентированный мультиграф (рис. 1) в виде объединения некоторого количества односвязных подграфов G = (G1ÈG2È...).
Каждой вершине соответствует экземпляр сущности. Представление мультиграфа в виде совокупности подграфов позволяет моделировать сложный характер инфицирования, когда, например, один больной экземпляр способен инфицировать других несколькими различными инфекциями (возможно, с различными вероятностями и при соблюдении различных условий).
Модели подграфов
Разрабатываемая система способна генерировать и использовать подграфы миров, имеющие следующие структурные свойства (рис. 2).
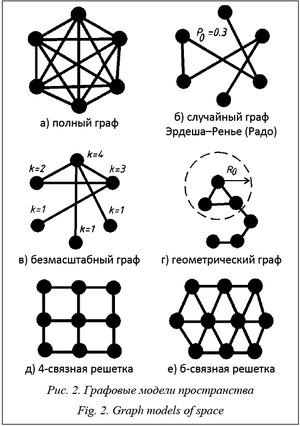
1. Полный граф, в котором каждая вершина свя- зана со всеми остальными. В полном графе из n вершин присутствуют все  возможных ребер. Такая топология характерна прежде всего для моделей, описывающих поведение программных сущностей в глобальных информационных сетях. Например, сетевые черви типа I-Worm.Msblast (2002 г.) способны напрямую обращаться к любому узлу сети Интернет, имеющему IP-адрес, а мобильные черви ComWarrior – к любому мобильному телефону в мире, имеющему номер в сетях сотовой связи [4, 9].
возможных ребер. Такая топология характерна прежде всего для моделей, описывающих поведение программных сущностей в глобальных информационных сетях. Например, сетевые черви типа I-Worm.Msblast (2002 г.) способны напрямую обращаться к любому узлу сети Интернет, имеющему IP-адрес, а мобильные черви ComWarrior – к любому мобильному телефону в мире, имеющему номер в сетях сотовой связи [4, 9].
2. Регулярные (гомогенные) графы типа решетки. Такая топология используется для решения различных задач в области теории перколяции, например, при исследовании распространения жидкости через пористые среды, взаимной диффузии металлов и пр. Параметром таких графов является связность, то есть постоянное количество соседей для каждой вершины.
3. Случайные графы общего вида (они же графы Эрдеша–Реньи, они же графы Радо) – подграфы полных графов, в которых ребро между двумя любыми вершинами существует с постоянной вероятностью P0 (и, разумеется, отсутствует с вероятностью 1–P0). Полное количество ребер в таком графе из n узлов 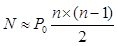 , а степени (валентности) вершин k распределены по Пуассону:
, а степени (валентности) вершин k распределены по Пуассону: 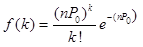 . В работе [10] рассмотрены методы построения графов Радо с наперед заданными средней степенью вершин
. В работе [10] рассмотрены методы построения графов Радо с наперед заданными средней степенью вершин  или средним коэффициентом кластеризации
или средним коэффициентом кластеризации 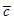 .
.
4. Безмасштабные случайные графы, то есть графы, обладающие характерной структурной особенностью: немногие вершины обладают большой валентностью, а многие – малой. Более конкретно: распределение валентностей вершин подчиняется экспоненциальному закону f(k) = k–g, где 2 £ g £ 3. Графы такого типа служат моделями социальных, транспортных, инженерных и коммуникационных сетей, их свойства очень активно изучаются в последние десятилетия. Методы генерации таких сетей опираются на алгоритмы предпочтительного присоединения вершин [11], а в работе [12] рассмотрены подходы к генерации случайных безмасштабных графов с заранее заданными статистическими характеристиками.
5. Геометрические случайные графы (RGG), то есть графы, структурные свойства которых определяются некоторыми геометрическими отношениями между вершинами. Обычно они служат моделями специальных (ad hoc) сетей. В разрабатываемой системе применяется разновидность геометрических графов, в которой наличие ребра между двумя вершинами с индексами i и j зависит от расстояния Rij между этими вершинами. Метрика при этом может быть разной: евклидовой 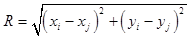 , тороидальной и т.п. Различной может быть и зависимость топологии от R. Например, для технических сетей (типа сетей сотовой связи) характерно наличие жесткой границы: если расстояние между двумя вершинами не превышает R0, то ребро между ними существует, иначе – нет. Для моделирования отношений в живой природе (например, при взаимодействии двух существ – здорового и больного воздушно-капельной инфекцией) характерна ситуация, когда вероятность P0 наличия ребра обратно-пропорциональна R. Конкретный вид этой зависимости может быть линейным P0(R) = 1 – R, эллиптическим
, тороидальной и т.п. Различной может быть и зависимость топологии от R. Например, для технических сетей (типа сетей сотовой связи) характерно наличие жесткой границы: если расстояние между двумя вершинами не превышает R0, то ребро между ними существует, иначе – нет. Для моделирования отношений в живой природе (например, при взаимодействии двух существ – здорового и больного воздушно-капельной инфекцией) характерна ситуация, когда вероятность P0 наличия ребра обратно-пропорциональна R. Конкретный вид этой зависимости может быть линейным P0(R) = 1 – R, эллиптическим  параболическим P0(R) = 1 – Rm (при m > 1) и т.п. Порог связности для геометрических графов
параболическим P0(R) = 1 – Rm (при m > 1) и т.п. Порог связности для геометрических графов  . В работе [10] рассмотрены подходы к генерации случайных географических графов с заранее заданными статистическими характеристиками. Важно, что топология ad hoc-графов может изменяться во времени, отражая тем самым способность сущностей перемещаться в пространстве относительно друг друга, устанавливая и теряя отношение близости. Известно, что направление движения людей an mass распределено равномерно, а расстояние, на которое проис- ходит движение, подчинено закону Леви [13].
. В работе [10] рассмотрены подходы к генерации случайных географических графов с заранее заданными статистическими характеристиками. Важно, что топология ad hoc-графов может изменяться во времени, отражая тем самым способность сущностей перемещаться в пространстве относительно друг друга, устанавливая и теряя отношение близости. Известно, что направление движения людей an mass распределено равномерно, а расстояние, на которое проис- ходит движение, подчинено закону Леви [13].
6. Наконец, ad hoc-графы, загружаемые извне, например, сгенерированные средствами специаль- ной программы, сопоставляющей топологию графа какой-нибудь конкретной геометрической структуре – местности или интерьеру [14].
Агентные модели сущностей
Определяющей особенностью агентных и мультиагентных методов имитационного моделирования является использование агентов – програм- мных моделей экземпляров сущностей, обла- дающих автономностью, индивидуальностью и способностью взаимодействия с другими агентами и внешней средой. Каждый агент обладает определенным набором свойств, которые в терминах объектно-ориентированного программирования можно отнести к двум классам: атрибуты и методы. Работа методов зависит от значений атрибутов, которые, в свою очередь, могут изменяться в результате работы методов. Инфицирование заключается в копировании некоторого набора свойств (атрибутов и методов) из одного агента в другой, после чего инфицированный агент сам способен самостоятельно инфицировать других агентов.
В алгоритмах действия инфицированных агентов можно выделить три основных аспекта: состояние, поиск целей, алгоритм инфицирования.
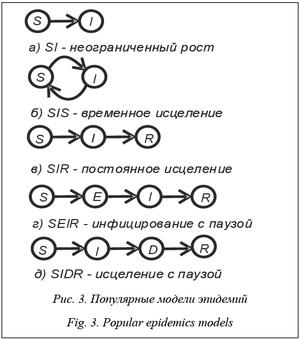
Состояние. Под состоянием понимается набор признаков, характеризующих способность к инфицированию той или иной инфекцией либо, наоборот, восприимчивость (или невосприимчивость) к той или иной инфекции. Пример набора состояний {I, S, R}, характерных для развития простых интернет-эпидемий, рассмотрен выше. Можно расширить его за счет состояний E – инфицирован, но не инфицирует, D – инфицирован, но неисцелен и т.п. Следует учесть, что биологические аналогии не всегда корректны. Так, например, при моделировании лесного пожара состоянию R, скорее всего, соответствует не исцеление, а разрушение дерева.
Различные модели перехода сущности из состояния в состояние (SI, SIS, SIR, SEIR, SIDR и др.) (рис. 3) изучаются многие десятилетия (см., например, работу [15]), и разрабатываемая система, безусловно, должна поддерживать как эти, так и иные, более изощренные модели.
Поиск целей. Важным аспектом моделирования процесса инфицирования является алгоритм поиска целей (то есть восприимчивых к инфекции агентов). Поиск выполняется среди доступных агентов, то есть тех, которым соответствуют вершины подграфа, инцидентные инфицирующей. В работах [9, 16] рассмотрено большое количество стратегий поиска, которые могут быть сведены к пяти основным.
1. Линейный поиск. Инфицирующие агенты выполняют последовательный перебор всех (или выделенного подмножества) доступных им агентов, пытаясь их инфицировать. Это наименее эффек- тивная стратегия, которая, однако, находит применение в примитивных сетевых червях (например Net-Worm.Cholera [9]).
2. Случайный поиск. Инфицирующие агенты выполняют случайный перебор всех (или выделенного подмножества) доступных им агентов, пытаясь их инфицировать. Это наиболее популярная и хорошо изученная стратегия, использованная множеством интернет-червей (например I-Worm.Red Code.b [7, 9]).
3. Поиск по списку. Инфицирующие агенты выполняют последовательный или случайный перебор выделенного подмножества доступных им агентов, восприимчивость к инфекции которых известна заранее. Данная стратегия является, например, элементом субоптимальной стратегии поведения гипотетического червя Уорхола [7].
4. Контратака. Инфицирующий агент выполняет инфицирование только тех агентов, которые, в свою очередь, попытались инфицировать его. Такая стратегия характерна для сетевых контрчервей [9], но можно найти ее аналогии и в жизни – например, когда врач оказывает медицинскую помощь только чихающим на него пациентам.
5. Одновременное инфицирование. Стратегия, имеющая биологические и природные аналогии, например, когда распространение огня от горящего дерева происходит сразу на все близко расположенные деревья. При моделировании может быть реализована как частный случай линейного поиска или случайного поиска с нулевыми затратами времени на сканирование.
В реальности встречаются как упомянутые стратегии в чистом виде, так и их комбинации. Например, червь Net-Worm.Win32.Lovesan с вероятностью 0,6 использовал стратегию случайного поиска и с вероятностью 0,4 – линейного [9]. А в работе [17] рассматривается алгоритм работы гипотетического самообучающегося червя, самостоятельно выбирающего стратегию поиска в зависимости от накопленной статистики удачных и неудачных попыток инфицирования.
Система моделирования поддерживает как базовые стратегии поиска, так и их несложные комбинации.
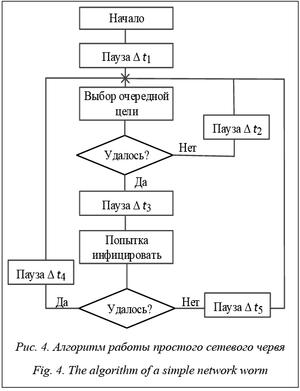 Алгоритм инфицирования. Этот аспект характеризует, в первую очередь, темпоральные характеристики работы инфицирующей сущности, от которых зависят темпоральные характеристики развития всей эпидемии. Например, в алгоритме работы дискретно-событийной модели простого сетевого червя (рис. 4) важную роль играют пять настраиваемых темпоральных атрибутов, позволяющих управлять таким параметром эпидемии, как коэффициент размножения β, то есть средним количеством инфицирований, выполняемых в единицу времени [7, 18].
Алгоритм инфицирования. Этот аспект характеризует, в первую очередь, темпоральные характеристики работы инфицирующей сущности, от которых зависят темпоральные характеристики развития всей эпидемии. Например, в алгоритме работы дискретно-событийной модели простого сетевого червя (рис. 4) важную роль играют пять настраиваемых темпоральных атрибутов, позволяющих управлять таким параметром эпидемии, как коэффициент размножения β, то есть средним количеством инфицирований, выполняемых в единицу времени [7, 18].
В общем случае эти атрибуты не являются константами и значение их может зависеть, например, от количества ранее уже инфицированных сущностей. Это позволяет воспроизводить, в частности, так называемые двухфакторные модели эпидемий, учитывающие влияние падения (в результате перегрузки) пропускной способности линий связи между узлами коммуникационной сети.
Реализация
Разработка и реализация среды моделирования выполняется преподавателями и студентами Самарского университета на инициативной основе в рамках курсового и дипломного проектирования. На текущий момент многочисленные варианты реализации представлены в виде набора исследовательских прототипов, имеющих общую структурную организацию (рис. 5).

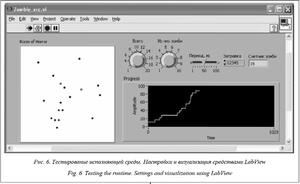
Ядром системы является исполняющая среда, оформленная в виде динамически загружаемой библиотеки для операционной системы Windows. Основное назначение – дискретно-событийная интерпретация модельных образов моделируемых вселенных (ММ), сформированных на этапе описания конкретного имитационного эксперимента. Во время имитационного эксперимента собираются необходимые характеристики моделируемых процессов, возможна их (процессов) демонстрационная визуализация (рис. 6).
Построение ММ выполняется из отдельных компонентов, собранных в БА – библиотеке алгоритмов работы агентов, и формируемых при помощи ГГ – генератора графов. БА и ГГ также оформлены в виде динамически загружаемых библиотек.
По итогам выполнения эксперимента подсистема обработки результатов позволяет рассчитать необходимые характеристики (например, усредненные кривые развития эпидемий), предназначенные для дальнейших визуализации и протоколирования.
Поскольку интерфейс доступа к DLL стандартизован, агрегация всех программных компонентов в единое целое может быть выполнена по-разному: путем компоновки с собственным программным проектом или при помощи подключения к какой-нибудь готовой инструментальной среде (рис. 6).
Заключение
В статье рассмотрены основные подходы к мультиагентному моделированию эпидемий (то есть процессов инфицирования одних сущностей со стороны других), характерных для технических сетей и живой природы, а также описаны устройство и принцип действия моделирующей программной среды, основанной на этих подходах. Основной особенностью, отличающей данную разработку от аналогов, является возможность моделирования развития эпидемий в мирах с динамически изменяющимися законами, что позволяет получать более адекватные результаты.
Литература
1. Климентьев К.Е., Помянский Р.А. Три подхода к моделированию сетевых эпидемий // Перспективные информационные технологии в научных исследованиях, проектировании и обучении (ПИТ 2012): тр. науч.-технич. конф. с междунар. участием. Самара: Изд-во СамНЦ РАН, 2012. С. 31–34.
2. Кондратьев М.А. Методы прогнозирования и модели распространения заболеваний // Компьютерные исследования и моделирование. 2013. Т. 5. № 5. С. 863–882.
3. Улыбин А.В., Арзамасцев А.А. Имитационное моделирование развития инфекции с использованием агентного подхода // Вестн. Тамбовского ун-та. Сер.: Естествен. и технич. науки. 2010. Т. 15. № 2. С. 614–619.
4. Channakeshava K. High performance, scalable, and expressive modeling environment to study mobile malware in large dynamic networks. PhD Thes. Virginia Polytechnic Inst., 2010, 142 p.
5. Smith R., Munz P., Hudea I., Imad J. When zombies attack: mathematical modeling of an outbreak of zombie infection. Infectious Disease Modelling Research Progress. 2009, pp. 133–157.
6. Tanachaiwiwat S., Helmy A. VACCINE: War of the worms in wired and wireless networks. IEEE INFOCom, 2006.
7. Weaver N.C. Warhol Worms: The potential for very fast internet plagues? 2001. URL: http://www1.icsi.berkeley.edu/ nweaver/papers/warhol/warhol.html (дата обращения: 11.12.2017).
8. Карпов Ю.Г. Имитационное моделирование систем. Введение в моделирование с AnyLogic 5. СПб: БХВ-Петербург, 2006. 400 с.
9. Климентьев К.Е. Компьютерные вирусы и антивирусы: взгляд программиста. М.: ДМК-Пресс, 2013. 656 с.
10. Климентьев К.Е. Случайные графы как модель среды распространения и взаимодействия саморазмножающихся объектов // Изв. Самарского научного центра РАН. 2015. Т. 17. № 2. С. 1021–1025.
11. Берновский М.М., Кузюрин Н.Н. Случайные графы, модели и генераторы безмасштабных графов // Тр. ИСП РАН. 2012. Т. 22. С. 419–434.
12. Юдин Е.Б. Генерация случайных графов предпочтительного связывания // Омский науч. вестн. 2010. № 2. С. 7–13.
13. Gonzalez M., Hidalgo C., Barabasi A. Understanding Individual Human Mobility Patterns. Nature, 2008, vol. 453, pp. 779–783.
14. Климентьев К.Е. Применение ГИС-технологий при исследовании распространения вредоносных программ // Геоинформационные технологии в проектировании и создании корпоративных информационных систем. Уфа: Изд-во УГАТУ, 2012. С. 130–133.
15. Котенко И.В., Воронцов В.В. Аналитические модели распространения сетевых червей // Тр. СПИИРАН. 2007. Вып. 4. С. 208–224.
16. Zou C., Towsley D., Gong W. On the performance of internet worm scanning strategies. Technican Report TR-03-CSE-07 of Univ. Massachusetts, Amherst, 2007, 16 p.
17. Chen Z., Ji C. A self-learning worm using importance scanning. ACM CSS Workshop on Rapid Malcode (WORM'05), 2005, pp. 22–29.
18. Kephart J.O., White S.R. Directed-graph epidemiological models of computer viruses. Proc. 1991 IEEE Comp. Society Sympos. on Research in Security and Privacy. Oakland, California, 1991, pp. 343–359.
19. Климентьев К.Е. Аналитические модели взаимодействия мобильных агентов // Перспективные информационные технологии в научных исследованиях, проектировании и обучении (ПИТ 2013): тр. науч.-технич. конф. с междунар. участием. Самара: Изд-во СамНЦ РАН, 2013. С. 54–56.
20. Лери М.М., Павлов Ю.Л. Лесной пожар на случайном графе со сгораемыми ребрами // Ученые записки Петрозавод- ского гос. ун-та. 2013. № 2. С. 96–99.



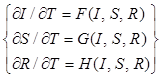 ,
,

 возможных ребер. Такая топология характерна прежде всего для моделей, описывающих поведение программных сущностей в глобальных информационных сетях. Например, сетевые черви типа I-Worm.Msblast (2002 г.) способны напрямую обращаться к любому узлу сети Интернет, имеющему IP-адрес, а мобильные черви ComWarrior – к любому мобильному телефону в мире, имеющему номер в сетях сотовой связи [4, 9].
возможных ребер. Такая топология характерна прежде всего для моделей, описывающих поведение программных сущностей в глобальных информационных сетях. Например, сетевые черви типа I-Worm.Msblast (2002 г.) способны напрямую обращаться к любому узлу сети Интернет, имеющему IP-адрес, а мобильные черви ComWarrior – к любому мобильному телефону в мире, имеющему номер в сетях сотовой связи [4, 9].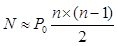 , а степени (валентности) вершин k распределены по Пуассону:
, а степени (валентности) вершин k распределены по Пуассону: 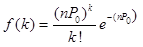 . В работе [10] рассмотрены методы построения графов Радо с наперед заданными средней степенью вершин
. В работе [10] рассмотрены методы построения графов Радо с наперед заданными средней степенью вершин  или средним коэффициентом кластеризации
или средним коэффициентом кластеризации 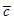 .
.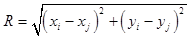 , тороидальной и т.п. Различной может быть и зависимость топологии от R. Например, для технических сетей (типа сетей сотовой связи) характерно наличие жесткой границы: если расстояние между двумя вершинами не превышает R0, то ребро между ними существует, иначе – нет. Для моделирования отношений в живой природе (например, при взаимодействии двух существ – здорового и больного воздушно-капельной инфекцией) характерна ситуация, когда вероятность P0 наличия ребра обратно-пропорциональна R. Конкретный вид этой зависимости может быть линейным P0(R) = 1 – R, эллиптическим
, тороидальной и т.п. Различной может быть и зависимость топологии от R. Например, для технических сетей (типа сетей сотовой связи) характерно наличие жесткой границы: если расстояние между двумя вершинами не превышает R0, то ребро между ними существует, иначе – нет. Для моделирования отношений в живой природе (например, при взаимодействии двух существ – здорового и больного воздушно-капельной инфекцией) характерна ситуация, когда вероятность P0 наличия ребра обратно-пропорциональна R. Конкретный вид этой зависимости может быть линейным P0(R) = 1 – R, эллиптическим  параболическим P0(R) = 1 – Rm (при m > 1) и т.п. Порог связности для геометрических графов
параболическим P0(R) = 1 – Rm (при m > 1) и т.п. Порог связности для геометрических графов  . В работе [10] рассмотрены подходы к генерации случайных географических графов с заранее заданными статистическими характеристиками. Важно, что топология ad hoc-графов может изменяться во времени, отражая тем самым способность сущностей перемещаться в пространстве относительно друг друга, устанавливая и теряя отношение близости. Известно, что направление движения людей an mass распределено равномерно, а расстояние, на которое проис- ходит движение, подчинено закону Леви [13].
. В работе [10] рассмотрены подходы к генерации случайных географических графов с заранее заданными статистическими характеристиками. Важно, что топология ad hoc-графов может изменяться во времени, отражая тем самым способность сущностей перемещаться в пространстве относительно друг друга, устанавливая и теряя отношение близости. Известно, что направление движения людей an mass распределено равномерно, а расстояние, на которое проис- ходит движение, подчинено закону Леви [13].



