Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Математическая модель активности пользователей программного обеспечения
Аннотация:В статье рассматриваются проблемы удобства использования ПО. Удобство использования является одним из основных критериев качества ПО в целом. Существуют различные подходы и методики, применяемые для анализа удобства использования программных продуктов, однако большинство из них основывается на эвристическом подходе, то есть на заранее собранных рекомендациях и гипотезах относительно того, как пользователь взаимодействует с программным интерфейсом. По мнению авторов, одна из основных проблем при разработке формальных методов оценки удобства использования – отсутствие формализованного представления данных активности пользователей программных продуктов. Целью исследования является разработка математической модели активности пользователей ПО. В основу исследования положена популярная в современной научной литературе идея о том, что индикатором проблем удобства использования может быть наличие часто повторяемых одинаковых последовательностей действий пользователей. В работе кратко рассматриваются подходы, применяемые при оценке удобства использования пользовательских интерфейсов, основанные на идее поиска закономерностей и шаблонов в поведении пользователей. Показано, что задачу поиска шаблонов поведения пользователей можно представить как задачу поиска последовательных шаблонов из области интеллектуального анализа данных и применять соответствующие методы. Вводится ряд формальных определений в области представления данных активности пользователей. Предлагается математическая модель активности пользователей ПО, основанная на теории последовательных шаблонов для предметной области оценки удобства использования. Данная модель может быть применена при автоматизированной оценке эффективности удобства пользовательских интерфейсов.
Abstract:The article describes software usability problems. According to ISO 9241-11:1998, usability is one of the main criteria of software quality. There are different approaches and methods to analyze the software usability. However, most of them are based on the heuristic approach that is on the previously collected recommendations and hypotheses about how a user interacts with a software interface. According to the authors, one of the main problems in the development of formal methods of usability evaluation is the lack of formalized data representation. The aim of the research is to develop a software user activity mathematical model. The research is based on the idea, which is popular in modern scientific literature, that indicator of usability problems is oft-repeated similar sequences and patterns. The paper briefly describes the approaches used in software usability evaluation. It’s shown that the task of repeated pattern searching might be represented as the task of sequential pattern mining from the data mining area. The paper introduces a number of formal definitions for user activity data. The authors suggest a software user activity mathematical model based on the sequential patterns theory for a usability evaluation subject area. This model can be used for automatic usability efficiency evaluation of user interfaces.
| Авторы: Сытник А.А. (shulga@sstu.ru) - Саратовский государственный технический университет им. Ю.А. Гагарина (профессор, зав. кафедрой ), Саратов, Россия, доктор технических наук, Шульга Т.Э. (shulga@sstu.ru) - Саратовский государственный технический университет им. Ю.А. Гагарина (доцент, профессор), Саратов, Россия, доктор физико-математических наук, Данилов Н.А. (shulga@sstu.ru) - Саратовский государственный технический университет им. Ю.А. Гагарина (аспирант ), Саратов, Россия, Гвоздюк И.В. (shulga@sstu.ru) - Саратовский государственный технический университет им. Ю.А. Гагарина (аспирант ), Саратов, Россия | |
| Ключевые слова: математическая модель активности пользователей по, последовательные шаблоны, пользовательский интерфейс, эффективность удобства использования, удобство использования |
|
| Keywords: mathematical model of software user activity, sequential patterns, user interface, usability efficiency, usability |
|
| Количество просмотров: 5431 |
Статья в формате PDF Выпуск в формате PDF (29.74Мб) |
Уровень удобства использования программного интерфейса влияет на качество всего ПО в целом. Признаком недостаточного уровня удобства использования является наличие проблем взаимодействия пользователя с пользовательским интерфейсом. Они могут быть связаны либо со сложностью формулирования плана действий (принятия решений, что делать дальше), либо с непониманием ответа системы (как изменения в интерфейсе связаны с выполненными действиями) [1]. Проблемы взаимодействия в большинстве случаев можно определить по наличию в данных активности пользователей определенных последовательностей действий (шаблонов). Для их обнаружения применяются различные методы анализа собираемых данных – как требующие ручного анализа (например, тепловые карты [2, 3]), так и использующие алгоритмы автоматического анали- за [1] на основе шаблонов, выявленных иссле- дователями ранее [4–6]. Автоматический анализ экономит время и деньги, так как эксперты вместо анализа всех данных фокусируют внимание на отдельных областях пользовательского интерфейса, где были выявлены соответствующие шаблоны. На настоящий момент в открытых научных ис- точниках не удалось найти формализованное пред- ставление данных активности пользователей ПО. В статье представлена разработанная авторами математическая модель активности пользователей ПО. Эта модель может найти применение при оценке удобства пользовательских интерфейсов. Целями являются максимальная формализация оценки удобства использования и формирование критериев для повышения эффективности взаимодействия пользователей с пользовательским интерфейсом. Шаблоны поведения пользователя По мнению многих исследователей (например, авторов [1, 4–6]), индикатором проблем удобства использования может являться наличие часто повторяемых одинаковых последовательностей действий. Они могут означать, что пользователь пытается достичь цели и каждый раз терпит неудачу. Например, пользователь пытается взаимодействовать с изображением, которое он принял за кноп- ку [1], или пользователь нажимает кнопку и каждый раз получает ошибку. В работе [4] выделен ряд шаблонов, связанных с выполнением пользователем поставленных задач, например, шаблон «Отмена действия», когда поль- зователь отменяет действие сразу после его выполнения, или шаблон «Повторение действий», когда пользователь часто повторяет простые действия (клики мыши или нажатие клавиш). Наличие второго шаблона может означать недостаточную отзывчивость интерфейса, которая ошибочно приводит пользователя к мысли, что система не распознает его действие. Отдельные исследователи предлагают отслеживать более простые индикаторы: количество вызовов онлайн-справки, количество действий отмены, частое открытие-закрытие выпадающих списков, нажатие одной и той же кнопки более одного раза и т.д. [5]. Другие исследователи основываются на обнаружении проблем поиска информации пользователем в процессе просмотра веб-сайта [6]. Например, выделяется шаблон вертикального или горизонтального перемещения курсора мыши. В процессе визуального поиска на странице пользователь обычно перемещает курсор вслед за элементами, а значит, тратит много времени на поиск элемента. Перечисленные методы поиска шаблонов поведения пользователей имеют много общего с задачей поиска последовательных шаблонов из области интеллектуального анализа данных [7]. В большинстве случаев все шаблоны являются последовательными, варьируются лишь анализируемые события. Однако данные активности пользователей почти всегда представляют собой не короткие транзакции, а большие наборы действий, которые в большинстве случаев невозможно корректно разделить на поднаборы [2, 3]. Поиск последовательных шаблонов давно и активно применяется в области торговли [8]. Поиск наиболее частых наборов позволяет получать информацию о том, через какой промежуток времени после покупки товара «А» человек наиболее склонен купить товар «Б» или в какой последовательности приобретаются товары. Получаемые закономерности в действиях покупателей можно использовать для персонализации клиентов, стимулирования продаж определенных товаров, управления запасами [8]. Это позволяет, с одной стороны, увеличить продажи, с другой – предложить клиентам товар, который, скорее всего, будет им интересен, а значит, минимизировать их временные затраты на поиск. При проектировании пользовательского интерфейса в соответствии со стандартами ГОСТ-28806-90 и ISO 9241-11:1998 аналогичным образом требуется максимизировать результативность (точность и полноту достижения пользователем поставленных целей, успешность выполнения промежуточных задач) и эффективность (отношение израсходованных ресурсов к точности и полноте, с которой пользователи достигают поставленных целей). Как уже отмечалось, одной из возможных при- чин появления регулярно повторяющихся шабло- нов в данных активности пользователей является наличие ошибок или затруднений при взаимодействии с интерфейсом. В этом случае может наблюдаться снижение и результативности, и эффективности пользователей. Следовательно, уменьшение числа подобных шаблонов снижает риск возникновения ошибок. Другой возможной причиной наличия повторяющихся шаблонов в данных активности пользователей является потребность выполнения одних и тех же повторяющихся цепочек действий для выполнения поставленных задач. Закономерно, что автоматизация промежуточных действий уменьшает затраты ресурсов. Следовательно, чем меньше пользователь совершает однотипных цепочек действий, тем меньше он затрачивает ресурсов, а значит, тем эффективнее взаимодействие. Конечно, при этом отмечается, что повторяющиеся шаблоны могут быть образованы из-за повторяющихся задач, которые либо невозможно или нецелесообразно автоматизировать, либо являются нормальным корректным поведением [1]. Поэтому требуется понимание семантики шаблонов и конкретных действий. Данные активности пользователей Введем несколько основных понятий, необходимых для формализации представления активности пользователей применительно к области оценки удобства использования. Событие – факт, зафиксированный в определенный момент времени при взаимодействии определенного пользователя на определенном устройстве с программным пользовательским интерфей- сом [9]. Событие обладает непустым уникальным набором атрибутов: пользователь, устройство, время, тип события (например, событие действия, командное событие) и специальные атрибуты, зависящие от типа события. Например, событие клика мыши может содержать наименование клавиши (левая, правая), тип клика (одинарный, двойной), координаты положения курсора мыши и т.д. Событие исполнения команды (командное событие) может содержать наименование кнопки, наименование команды, способ исполнения (клик мыши, горячая клавиша, клавиша Enter). Обозначим E множество всех зафиксированных событий: E = {e1, …, en}, где {ei}, Сессия – зафиксированный временной промежуток, в течение которого пользователь взаимодействовал с программной системой [9]. В рамках сессии все события накапливаются и хранятся в хронологическом порядке. Важно отметить, что каждое событие является уникальным и может быть включено только в одну сессию. Определим размещение – упорядоченный набор элементов множества либо с повторениями, либо без повторений в соответствии с общепринятым определением [10]. Размещение будем заключать в треугольные скобки. Тогда, если обозначать элементы множества целыми числами, размещения будут записаны в виде á1, 2, 3, 1ñ. Обозначим S множество всех зафиксированных сессий: S = {s1, …, sm}, где {si}, Особо отметим, что каждое событие обладает непустым уникальным набором атрибутов, следовательно, является уникальным. Сессия представляет собой размещение элементов множества E без повторений: si = 〈ei1, …, eij〉, где {eij}, Множество E формируется в результате объединения всех множеств сессий, полученных из данных активности пользователей. При этом любое событие принадлежит хотя бы одной сессии: ∀e Î E, ∃s Î S, e Î s, где E – множество всех зафиксированных событий; e – отдельное событие; S – множество всех зафиксированных сессий; s – отдельная сессия. Классификация событий Заметим, что в размещении без повторений, которым изначально является сессия, невозможно существование регулярно повторяющихся шаблонов как упорядоченных подмножеств. Поэтому требуется предварительная классификация всех событий. Классом событий будем считать произвольную совокупность событий, обладающих каким-либо определенным свойством или признаком. Например, возможна классификация событий по типу, по названию исполненной команды (для командных событий), по области пользовательского интерфейса (в области верхнего меню, в основной рабочей области). Обозначим CE множество всех определенных классов событий: CE = {c1, …, ck}, {ci}, где Для классификации событий вводится однозначная классифицирующая функция f, которая может быть записана как f : E → CE. Правила классификации и набор классов, безусловно, должны определяться экспертом. Заметим, что в зависимости от целей исследования часть событий может игнорироваться. Например, эксперта могут интересовать лишь командные события, то есть связанные с вызовом какой-либо команды. В этом случае будем говорить, что про- изведена фильтрация событий. В дальнейшем под событием будем понимать событие именно после классификации, то есть класс события. Соответственно, под сессией будем понимать сессию после классификации и фильтра- ции, так как поиск регулярных последовательных шаблонов невозможен до этих действий по причине уникальности каждого события. Обозначим S¢ множество всех зафиксированных сессий, после классификации и фильтрации S¢ = {s1¢, …, s¢m}, где Сессия после классификации представляет собой размещение элементов множества CE с повторениями: s¢i = 〈ci1, …, cij〉, где {сij}, Обозначим Например, пусть имеется сессия s = 〈клик1, командаА, клик2, движение1, командаА, командаБ〉. Определим классифицирующую функцию:
Применив классифицирующую функцию, получим сессию s¢ = 〈3, 1, 3, 3, 1, 2〉. Допустим, отфильтровав все события класса 3, получим сессию s¢ = 〈1, 1, 2〉. Поддержка последовательного шаблона Теория последовательных шаблонов подразумевает наличие множества кандидатов, для которых проверяется уровень поддержки. Для начала определим понятия шаблона и поддержки шаблона для одной сессии. Обозначим P множество кандидатов последовательных шаблонов: P = {p1, …, pr}, где {pi}, Шаблон представляет собой размещение элементов множества CE с повторениями: pi = 〈ci1, …, cij〉, где {cij}, Будем считать длиной шаблона или сессии количество событий в указанном размещении, а также то, что шаблон p входит в сессию s¢, если все элементы p содержатся в s¢, при этом порядок элементов в подмножестве из s¢ соответствует порядку элементов p. Обозначим Шаблон p называется поддерживаемым сессией s¢, а следовательно, поддерживаемым пользователем, если количество вхождений Обозначим Таким образом, для одной сессии можно описать значение поддержки как долю содержания шаблона в сессии. Это необходимо для сравнения разных шаблонов по степени влияния на процесс взаимодействия пользователя с ПО, что невозможно сделать на основе лишь значения количества вхождений. Например, пусть имеется сессия 〈2, 1, 2, 1, 3, 2, 1, 2, 1, 3〉. Рассчитаем значения m и l для следующих шаблонов: p1 = 〈2, 1〉, m = 4, l = 0.8; p2 = 〈2, 1, 2, 1〉, m = 2, l = 0.8; p3 = 〈2, 1, 2, 1, 3〉, m = 2, l = 1; p4 = 〈3, 2, 1, 2, 1, 〉, m = 1, l = 0.5. Поддержка шаблона p1 совпадает с поддержкой p2 и равна 0.8. Однако поддержка шаблона p3 равна 1, то есть он полностью составляет сессию, а значит, является более вероятным кандидатом для пристального внимания эксперта. Повышение эффективности взаимодействия пользователя с программным интерфейсом с подобным шаблоном кардинально может повысить эффективность всего процесса работы с ПО в целом. Проанализируем, как меняются значения m и l при увеличении количества регулярных последовательностей событий. Для этого повторим набор событий в сессии: 〈2, 1, 2, 1, 3, 2, 1, 2, 1, 3, 2, 1, 2, 1, 3, 2, 1, 2, 1, 3〉. Рассчитаем значения m и l для следующих шаблонов: p1 = 〈2, 1〉, m = 8, l = 0.8; p2 = 〈2, 1, 2, 1〉, m = 4, l = 0.8; p3 = 〈2, 1, 2, 1, 3〉, m = 4, l = 1; p4 = 〈3, 2, 1, 2, 1, 〉, m = 3, l = 0.75. Поддержка шаблонов p1, p2 и p3 осталась прежней несмотря на увеличение количества вхождений. Количество вхождений p4 увеличилось в 3 раза, но поддержка – лишь на 0.25. Шаблон p3 по-прежнему составляет всю сессию, фактически полностью определяя взаимодействие пользователя с пользовательским интерфейсом, и оттого остается наиболее вероятным кандидатом для детального анализа экспертом. Учитывая, что сессий может быть любое количество, необходимо агрегировать значение поддержки, сохранив их семантику, а именно долю содержания шаблона в сессиях. Поэтому общая поддержка шаблона p множеством сессий рассчитывается как взвешенная средняя арифметическая. Обозначим
где S¢ – множество сессий после классификации и фильтрации; m – мощность множества S¢; Полученные формулы позволяют рассчитывать значение поддержки различных последовательных шаблонов активности пользователей. Простое сравнение числовых значений поддержки позволяет ранжировать шаблоны по степени приоритета для детального анализа. Математическая модель активности пользователей Для оценки эффективности взаимодействия пользователя с пользовательским интерфейсом необходимо относительно выбранных шаблонов рассчитать затраченные ресурсы пользователя. Однако шаблоны содержат не исходные события, а классы, не имеющие информации о реальной длительности временных интервалов между событиями. Для преобразования классов в затрачиваемое время вводится скалярная функция На данный момент авторы предлагают, чтобы функцию t определял эксперт на основе знаний о системе. Эксперт может воспользоваться известными моделями. Например, существует распространенный метод оценки эффективности интерфейса – GOMS (Goals, Operators, Methods, Selection Rules – Цели, Операторы, Методы, Правила выбора соответственно) [11]. Идея метода заключается в разбиении взаимодействия пользователя с интерфейсом на атомарные физические и когнитивные действия. Обладая знаниями о метриках каждой из таких составляющих, можно делать заключение об эффективности взаимодействия в целом: оценка эффективности интерфейса сводится к разбиению типовых задач на элементарные действия и сложе- нию метрик каждого из них. Метод GOMS вклю- чает в себя модель Keystroke-level Model (KLM) [11], которая выделяет следующие элементарные задачи и длительность каждой из них (рассчитанные на основе усредненных данных лабораторных испытаний): · K – нажатие на клавишу в зависимости от уровня владения клавиатурой: профессиональный наборщик – 0.08 сек., эксперт – 0.12 сек., частая работа с текстом – 0.20 сек., продвинутый пользователь – 0.28 сек., неуверенный пользователь – 0.5 сек., не знакомый с клавиатурой – 1.2 сек.; · P – указание курсором мыши на объект – 1.1 сек.; · B – нажатие или отпускание мыши – 0.1 сек.; · M – умственная подготовка, выбор дейст- вия – 1.2 сек.; · H – перемещение руки в исходное положение на клавиатуре – 0.4 сек; · R – ожидание ответа системы, зависящее от времени выполнения системой запрошенной операции. Оценка времени на решение задачи сводится к сложению продолжительностей каждой из простейших составляющих. Например, задача, состоящая из классов 〈P, P, B〉, потребует для завершения 2.3 сек. (1.1 сек. + 1.1 сек. + 0.1 сек.). Аналогично оценка времени, затрачиваемого на один шаблон, сводится к сложению продолжительности его составляющих и произведению полученной суммы на количество вхождений. Например, обозначим t(p) суммарные затраты времени пользователями на шаблон p для всего множества сессий и рассчитаем их: Таким образом, можно описать общую математическую модель активности пользователей: M = = {E, CE, f, S, S¢, P, Λ, t}, где E ={ei}, Данная модель может найти применение при оценке удобства использования пользовательских интерфейсов и для решения задач повышения эффективности взаимодействия пользователей с ПО. Имея значения поддержки и затрачиваемого времени для каждого шаблона, эксперт может сконцентрироваться на наиболее значимых из них для процесса работы пользователей с ПО в целом. Набор шаблонов при этом будет зависеть от целей проводимого анализа. Далее эксперт может выдвинуть гипотезы о необходимых изменениях в пользовательском интерфейсе для повышения эффективности взаимодействия пользователей с ПО. При принятии решений эксперту необходимо учитывать множество различных факторов: особенности ПО, психологические факторы использования ПО и особенности пользователей. Изменение пользовательского интерфейса повлечет изменение множеств событий, сессий и последовательных шаблонов, так как изменится последовательность действий, необходимых для достижения пользователями поставленных целей. Таким образом, можно утверждать, что задачей эксперта становится переход от текущей модели активности пользователей к новой, с иным составом сессий и шаблонов, следовательно, и иными значениями поддержки шаблонов и затратами времени пользователей. После внесения изменений в программный интерфейс возможны повторный сбор и анализ данных активности пользователей, что может подтвердить либо опровергнуть выдвинутую ранее гипотезу. Заключение В статье введены основные формальные определения в предметной области удобства использования и представлена математическая модель активности пользователей ПО. Предложенную математическую модель целесообразно использовать для решения задач повышения эффективности человеко-компьютерного взаимодействия, проектирования и создания пользовательских интерфейсов. Сформирована концептуальная задача для эксперта при использовании представленной математической модели как переход от текущей модели активности пользо- вателей к новой, с иным составом сессий и шаблонов, позволяющим судить о повышении эф- фективности взаимодействия пользователя с программным интерфейсом. В данный момент проводится анализ эффективности разработанной математической модели для различных типов интерфейсов программных систем. Литература 1. Siochi A.C., Ehrich R.W. Computer Analysis of User Interfaces Based on Repetition in Transcripts of User Sessions. ACM Transactions on Information Systems, 1991, vol. 9, no. 4, pp. 309–335. 2. Данилов Н.А., Шульга Т.Э. Метод построения тепловой карты на основе точечных данных об активности пользователя приложения // Прикладная информатика. 2015. Т. 10. № 2. С. 49–58. 3. Danilov N., Shulga T., Frolova N., Melnikova N., Vagari- na N., Pchelintseva E. Software usability evaluation based on the user pinpoint activity heat map. Advances in Intelligent Systems and Computing, 2016, vol. 465, pp. 217–225. 4. Balbo S., Goschnick S., Tong D., Paris C. Leading Usability Evaluations to WAUTER. Proc. 11th Australian World Wide Web Conf. (AusWeb), Gold Coast, Australia, Southern Cross Univ., 2005, pp. 279–290. 5. Swallow J., Hameluck D., Carey T. User interface instrumentation for usability analysis: a case study. CASCON’97, Toronto, Ontario, 1997. 6. Shah I. Event patterns as indicators of usability problems. Jour. of King Saud Univ., Comp. and Inform. Sci., 2008, pp. 31–43. 7. Mabroukeh N.R., Ezeife C.I. A taxonomy of sequential pattern mining algorithms. ACM Computing Surveys (CSUR), 2010, vol. 43, no. 1, article no. 3. 8. Aloysius G., Binu D. An approach to products placement in supermarkets using prefixspan algorithm. Jour. of King Saud Univ. Comp. and Inform. Sc., 2013, vol. 25, no. 1, pp. 77–87. 9. Данилов Н.А., Шульга Т.Э. Варианты использования онтологии для анализа юзабилити // Информационно-коммуникационные технологии в науке, производстве и образовании (ICIT-2016): матер. Междунар. науч.-практич. конф. Саратов. 2016. C. 160–167. 10. Виленкин Н.Я. Комбинаторика кортежей и множеств. Размещения с повторениями: В кн.: Популярная комбинаторика. М.: Наука, 1975. 208 с. 11. Card S., Moran T., Newell A. The keystroke-level model for user performance time with interactive systems. Communications of the ACM, 1980, vol. 23, no. 7, pp. 396–410. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=4402 |
Версия для печати Выпуск в формате PDF (29.74Мб) |
| Статья опубликована в выпуске журнала № 1 за 2018 год. [ на стр. 79-84 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Оптимизирующие стратегии визуализации данных в тактическом тренажере
- Акцентная визуализация в интерфейсах дополненной реальности
- Метод автоматизированного формирования семантической модели базы данных диалоговой системы
- Проектирование интерфейса программного обеспечения с использованием элементов искусственного интеллекта
- Естественно-языковой пользовательский интерфейс диалоговой системы
Назад, к списку статей



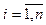 – отдельные события; n – мощность множества E.
– отдельные события; n – мощность множества E. – отдельные сессии; m – мощность множества S.
– отдельные сессии; m – мощность множества S.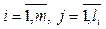 – отдельное событие i-й сессии; li – мощность размещения si.
– отдельное событие i-й сессии; li – мощность размещения si. – отдельный класс; k – мощность множества CE.
– отдельный класс; k – мощность множества CE.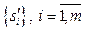 – отдельная сессия; m – мощность множества S¢.
– отдельная сессия; m – мощность множества S¢.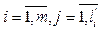 – отдельное событие i-й сессии; l¢i – мощность размещения s¢i.
– отдельное событие i-й сессии; l¢i – мощность размещения s¢i.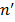 суммарное количество событий в сессиях после классификации и фильтрации:
суммарное количество событий в сессиях после классификации и фильтрации:  , где m – мощность множества S¢; l¢i – мощность размещения s¢i.
, где m – мощность множества S¢; l¢i – мощность размещения s¢i.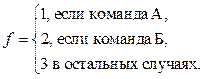
 – отдельный шаблон; r – мощность множества
– отдельный шаблон; r – мощность множества  .
. , cij Î CE – отдельное событие i-го шаблона; r – мощность множества P; qi – мощность размещения pi, то есть количество событий в шаблоне.
, cij Î CE – отдельное событие i-го шаблона; r – мощность множества P; qi – мощность размещения pi, то есть количество событий в шаблоне. количество вхождений шаблона p в сессию s¢, рассчитываемую как количество непересекающихся упорядоченных вхождений. Например, пусть имеются сессия 〈1, 2, 1, 2, 1, 2, 3, 1, 2, 1〉 и шаблон 〈1, 2, 1〉. Количество вхождений m будет равно 2, так как 3-й элемент сессии (1) уже участвовал при подсчете.
количество вхождений шаблона p в сессию s¢, рассчитываемую как количество непересекающихся упорядоченных вхождений. Например, пусть имеются сессия 〈1, 2, 1, 2, 1, 2, 3, 1, 2, 1〉 и шаблон 〈1, 2, 1〉. Количество вхождений m будет равно 2, так как 3-й элемент сессии (1) уже участвовал при подсчете. поддержку шаблона p сессией s¢, рассчитываемую следующим образом:
поддержку шаблона p сессией s¢, рассчитываемую следующим образом:  , где
, где 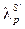 поддержку шаблона p множеством сессий S¢, рассчитываемую как
поддержку шаблона p множеством сессий S¢, рассчитываемую как
 – количество вхождений шаблона p в сессию si¢; q – длина шаблона p;
– количество вхождений шаблона p в сессию si¢; q – длина шаблона p; 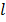 – длина сессии si¢; n¢ – суммарное количество событий в сессиях после классификации и фильтрации.
– длина сессии si¢; n¢ – суммарное количество событий в сессиях после классификации и фильтрации. , которая может быть записана следующим образом:
, которая может быть записана следующим образом: 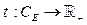 , где CE – множество всех определенных классов событий;
, где CE – множество всех определенных классов событий; 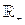 – множество положительных вещественных чисел.
– множество положительных вещественных чисел. , где {ci},
, где {ci},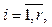 ci Î CE – отдельное событие шаблона.
ci Î CE – отдельное событие шаблона.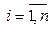 – множество событий с атрибутами; CE = {ci},
– множество событий с атрибутами; CE = {ci},  – множество классов событий; f: E ® CE – функция классификации событий; S = {si},
– множество классов событий; f: E ® CE – функция классификации событий; S = {si},  – множество сессий до классификации, si = áei1, …, eilñ,
– множество сессий до классификации, si = áei1, …, eilñ,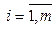 – сессия до классификации, l – длина i-й сессии;
– сессия до классификации, l – длина i-й сессии; 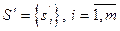 – множество сессий после классификации и фильтрации,
– множество сессий после классификации и фильтрации, 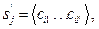
 – сессия после классификации и фильтрации, l¢ – длина i-й сессии после классификации и фильтрации; P = {pi},
– сессия после классификации и фильтрации, l¢ – длина i-й сессии после классификации и фильтрации; P = {pi}, 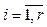 – множество последовательных шаблонов, pi = áci1, …, ciqñ,
– множество последовательных шаблонов, pi = áci1, …, ciqñ,  – последовательный шаблон;
– последовательный шаблон; 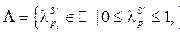
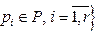 – множество значений поддержки последовательных шаблонов;
– множество значений поддержки последовательных шаблонов; 