Агрегирование информации является одним из перспективных направлений повышения качества и эффективности функционирования систем сбора и обработки информации о высокодинамичных объектах [1–5]. Сущность данного подхода состоит в выявлении распределения объектов в пространстве и представлении выявленного распределения в виде, удовлетворяющем потребителя. При этом в роли потребителя могут выступать как функциональные звенья системы сбора и обработки различных уровней, так и субъекты управления в системе старшего порядка.
За инструментальную основу методологии агрегирования принят математический аппарат теории нечетких множеств [6–8], обеспечивающий формализацию присущей исходным данным неопределенности в форме нечеткого описания характерных закономерностей. По своей сути задача агрегирования данных о высокодинамичных объектах представляет собой задачу распознавания групп объектов и включает следующие основные этапы:
- построение в имеющемся признаковом пространстве (совокупности признаковых пространств) множества объектов Х нечеткого отношения/отношений принадлежности Ri, i = 1, 2, …, и его/их преобразование в отношение строгого предпочтения либо адекватное ему, то есть {Ri} → RS, далее – отношение предпочтения;
- выделение на этой основе на множестве Х компактных подмножеств отметок, описывающих взаимосвязанную совокупность отображений объ- ектов, то есть RS: X ® UkXk, 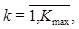 lim Kmax = = card X, и их представление потребителю.
lim Kmax = = card X, и их представление потребителю.
Нечеткое отношение принадлежности R строится на базе гипотезы о предварительном распределении объектов множества X на компактные группы и представляет собой нечеткое подмножество декартова произведения X×X вида MR = {(x, y)/(x, y) Î X ´ X, m(x, y)}, где m(x, y) → [0, 1] – характеристическая функция отношения между парой объектов [6–8]. Преобразование одного или нескольких исходных отношений принадлежности Ri заключается в придании результатному отношению RS свойств, обеспечивающих разбиение множества объектов X на непересекающиеся подмножества и выделение на каждом из них носителя отношения.
Обобщенный эффект от агрегирования по сравнению с традиционной технологией обработки информации о высокодинамичных объектах состоит в минимизации неизбежных информационных потерь и наиболее рельефно проявляется в условиях предельных информационных нагрузок на элементы системы сбора и обработки, функционирующей в жестком реальном масштабе времени [2–5].
В рамках общей схемы указанного подхода для решения конкретных задач в системе сбора и обработки могут применяться различные алгорит- мы [5]. Это различие может заключаться как в составе, так и в значениях учитываемых алгоритмами признаков объектов, а также в наборе и по- следовательности реализации вычислительных процедур. Вследствие этого алгоритмы могут приводить к различным результатам и характеризоваться различными затратами вычислительных ресурсов. Например, в зависимости от требований потребителя могут быть заданы различные параметры гипотезы о предварительном разбиении множества объектов на образы. Далее могут реализовываться как оптимальные, так и квазиоп- тимальные преобразования отношения принадлежности, требующие различных затрат процессорного времени и оперативной памяти. Причем важность параметров, определяющих различие алгоритмов, зависит от большого числа факторов и может быть определена лишь для конкретных ситуаций апостериорно, например, по результатам моделирования.
Обоснованный выбор рационального алго- ритма для гарантированного удовлетворения требований потребителя к качеству информации предполагает наличие сравнительных оценок получаемых результатов агрегирования. В этой связи актуальным представляется вопрос о подходе к получению таких оценок.
Известный подход к сравнению результатов агрегирования состоит в сопоставлении списков полученных агрегатов [5, 9]. При агрегировании информации о множествах объектов формирование списков связано с переходом от нечеткого описания таких множеств к их четкому представлению так называемыми эталонными объектами, являющимися носителями отношения при соответствующем уровне значимости. В этих условиях часть информации, присущей нечеткому описанию обстановки, теряется, описание обстановки загрубляется, поэтому для формирования адекватных сравнительных оценок результатов агрегирования, получаемых различными алгоритмами, их сравнение целесообразно проводить на основе результатов, получаемых на первом этапе, то есть на основе формируемых отношений предпочтения.
Пусть 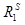 и
и 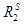 – отношения предпочтения на множестве X, построенные алгоритмами агрегирования A1 и A2, то есть
– отношения предпочтения на множестве X, построенные алгоритмами агрегирования A1 и A2, то есть 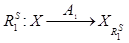 ,
,  Каждое отношение как результат работы алгоритма представлено соответствующей матрицей, то есть
Каждое отношение как результат работы алгоритма представлено соответствующей матрицей, то есть 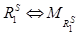 ,
, 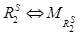 .
.
Необходимо сформировать такой подход F* к сравнению отношений 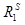 и
и 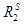 , что
, что
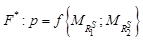 , (1)
, (1)
где p – показатель, характеризующий различие отношений 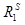 и
и 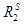 .
.
Исходя из целевого назначения, показатель p должен отражать различие в нечетких разбиениях множества X на непересекающиеся подмножества, полученные различными алгоритмами.
С точки зрения означенного требования матрицы нечетких отношений предпочтения 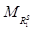 и
и  обладают определенной избыточностью, так как для каждого объекта x Î X существует N альтернатив, где N = card X. В соответствии с теоремой о декомпозиции [6–9], любое нечеткое отношение предпочтения RS, построенное на множестве X, индуцирует его иерархическую структуру, иными словами – стратификацию всех нечетких подмножеств. Исходя из этого такому отношению соответствует
обладают определенной избыточностью, так как для каждого объекта x Î X существует N альтернатив, где N = card X. В соответствии с теоремой о декомпозиции [6–9], любое нечеткое отношение предпочтения RS, построенное на множестве X, индуцирует его иерархическую структуру, иными словами – стратификацию всех нечетких подмножеств. Исходя из этого такому отношению соответствует 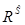 – нечеткое отношение, однозначно отражающее иерархическую структуру множества X на интервале уровня значимости a = [0, 1]. Данное отношение представляет собой нечеткое подмножество множества
– нечеткое отношение, однозначно отражающее иерархическую структуру множества X на интервале уровня значимости a = [0, 1]. Данное отношение представляет собой нечеткое подмножество множества 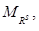 а его элементы в общем случае удовлетворяют условию
а его элементы в общем случае удовлетворяют условию
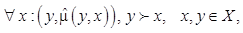
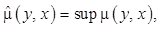 (2)
(2)
где y – носитель отношения для элемента х, вы- деляемый на интервале значимости функции принадлежности a = [0, L], L Î [0, 1]; m(y, x) – зна- чение функции принадлежности элемента y к элементу x на интервале значимости функции принадлежности a = [0, L].
При этом для корневого элемента иерархии, то есть элемента, являющегося носителем отношения при любом уровне значимости, (y, m(x, y)) = Æ.
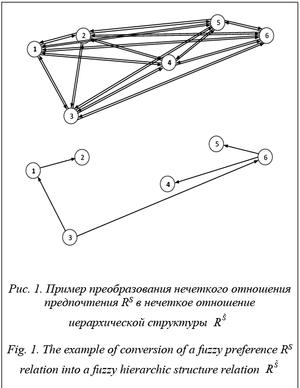 Граф
Граф 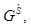 соответствующий полученному отношению, является деревом [10]. Его узлы – элементы множества Х, а дугам соответствуют значения функций принадлежности согласно условию (2) (рис. 1).
соответствующий полученному отношению, является деревом [10]. Его узлы – элементы множества Х, а дугам соответствуют значения функций принадлежности согласно условию (2) (рис. 1).
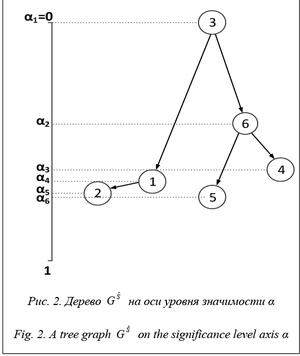
При расположении узлов дерева 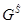 вдоль оси α с привязкой по уровню значимости отношения (рис. 2) каждому элементу множества X может быть поставлена в соответствие характеристика его значимости в заданной структуре предпочтений. Следовательно, при любом A, обеспечивающем построение на множестве Х отношения RS, данное отношение может быть отображено в точку N-мерного пространства отношений, то есть
вдоль оси α с привязкой по уровню значимости отношения (рис. 2) каждому элементу множества X может быть поставлена в соответствие характеристика его значимости в заданной структуре предпочтений. Следовательно, при любом A, обеспечивающем построение на множестве Х отношения RS, данное отношение может быть отображено в точку N-мерного пространства отношений, то есть
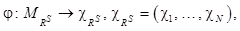
N = card X. (3)
 Таким образом, точка
Таким образом, точка 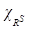 пространства отно- шений будет определяться суммой N ортогональных векторов, каждый из которых характеризует собой значимость соответствующего элемента x в нечеткой структуре предпочтений на множестве X, заданных отношением RS. В свою очередь, по-казателем различия отношений
пространства отно- шений будет определяться суммой N ортогональных векторов, каждый из которых характеризует собой значимость соответствующего элемента x в нечеткой структуре предпочтений на множестве X, заданных отношением RS. В свою очередь, по-казателем различия отношений 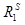 и
и 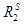 может служить евклидово расстояние между их отображениями в пространстве отношений [11]:
может служить евклидово расстояние между их отображениями в пространстве отношений [11]:
 . (4)
. (4)
Для оценки значимости элементов множества X в заданной структуре предпочтений каждой дуге g графа 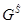 сопоставим вес β, определяемый как разность минимальных уровней значимости, при которых элементы, инцидентные указанной дуге, являются носителями отношения (рис. 3), то есть
сопоставим вес β, определяемый как разность минимальных уровней значимости, при которых элементы, инцидентные указанной дуге, являются носителями отношения (рис. 3), то есть

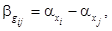 (5)
(5)
где 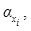
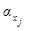 – уровни значимости, при которых элементы xi и xj, инцидентные дуге gij, становятся носителями отношения.
– уровни значимости, при которых элементы xi и xj, инцидентные дуге gij, становятся носителями отношения.
 Геометрически вес дуги интерпретируется как длина ее проекции на ось a. Численно он равен разности соответствующих функций принадлежности в матрице отношения предпочтения
Геометрически вес дуги интерпретируется как длина ее проекции на ось a. Численно он равен разности соответствующих функций принадлежности в матрице отношения предпочтения 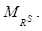
На этой основе каждому узлу графа 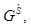 а соответственно и каждому элементу множества X, сопоставим его значимость
а соответственно и каждому элементу множества X, сопоставим его значимость 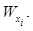 При этом будем учитывать то обстоятельство, что значимость элемента x определяется его местом в выявленной нечеткой иерархической структуре.
При этом будем учитывать то обстоятельство, что значимость элемента x определяется его местом в выявленной нечеткой иерархической структуре.
Значимость элементов xi, соответствующих корням поддеревьев 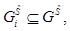 определим как
определим как
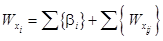 , (6)
, (6)
где βi – вес дуги, инцидентной корню поддерева 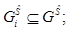
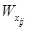 – значимость элемента xj, инцидентного корню xi поддерева
– значимость элемента xj, инцидентного корню xi поддерева 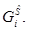
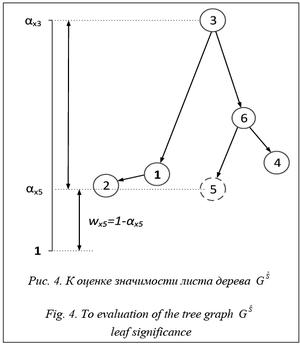
Листья графа  не имеют исходящих дуг [10]. Для соответствующих им элементов будем полагать
не имеют исходящих дуг [10]. Для соответствующих им элементов будем полагать
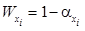 , (7)
, (7)
где 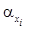 – минимальный уровень значимости, при котором элемент xi является носителем отноше- ния (рис. 4).
– минимальный уровень значимости, при котором элемент xi является носителем отноше- ния (рис. 4).
 В результате выполнения операций (2)–(7) каждому узлу графа
В результате выполнения операций (2)–(7) каждому узлу графа 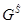 сопоставлено число
сопоставлено число 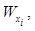 отражающее значимость элемента xi в заданной на множестве X нечеткой структуре предпочтений. На этой основе и выполняется отображение отношения RS в точку пространства отношений
отражающее значимость элемента xi в заданной на множестве X нечеткой структуре предпочтений. На этой основе и выполняется отображение отношения RS в точку пространства отношений
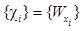 , (8)
, (8)
где χi – значение i-й координаты точки в N-мерном пространстве отношений.
Таким образом, сущность изложенного подхода к сравнению результатов, полученных алгоритмами агрегирования A1 и A2, состоит в следующем:
– представление результатов работы каждого алгоритма матрицей нечеткого отношения пред- почтения 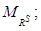
– выделение из каждой матрицы элементов отношения 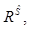 характеризующего нечеткую структуру предпочтений на множестве Х;
характеризующего нечеткую структуру предпочтений на множестве Х;
– получение отображений выделенных структур предпочтений в N-мерном пространстве;
– расчет расстояния между отображениями.
При таком подходе показатель p будет удовлетворять своему целевому назначению, то есть отражать любое различие в нечетких разбиениях множества X на непересекающиеся подмножества, получаемые различными алгоритмами. В этом смысле он определенным образом характеризует различие в качестве алгоритмов и может использоваться для получения сравнительных оценок при исследовании качества и эффективности алгоритмов, разработанных в рамках сформированной системы методов агрегирования информации о высокодинамичных объектах [5]. При этом, естественно, необходима определенная адаптация предложенного подхода к особенностям и условиям агрегирования информации на соответствующем этапе ее обработки, в частности – к форме алгоритмического представления отношения предпочтения, обеспечивающего разбиение множества объектов на непересекающиеся подмножества.
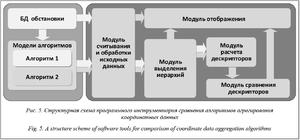 Так, в среде программирования MATLAB реализован программный инструментарий для формирования сравнительных оценок алгоритмов агрегирования координатных данных, реализующих нечеткую логику [12]. Структурно данный инструментарий включает в свой состав комплекс функциональных модулей (рис. 5) и алгоритмически сопряжен с архитектурой оцениваемых алгоритмов.
Так, в среде программирования MATLAB реализован программный инструментарий для формирования сравнительных оценок алгоритмов агрегирования координатных данных, реализующих нечеткую логику [12]. Структурно данный инструментарий включает в свой состав комплекс функциональных модулей (рис. 5) и алгоритмически сопряжен с архитектурой оцениваемых алгоритмов.
Модуль считывания и обработки исходных данных включает в свой состав комплекс функций, обеспечивающих считывание координат объектов из БД, содержащей сведения о реализациях обстановки и массивов матриц нечеткого предпочтения, формируемых сравниваемыми алгорит- мами по каждой реализации, а также ранжиро- вание матриц. Считывание координат объектов осуществляется для отображения текущей реализации исходной обстановки, а ранжирование матриц – для приведения результатов работы алгоритмов с различными наборами вычислительных процедур к единой форме представления отношения предпочтения.
Модуль выделения иерархий включает в свой состав комплекс функций, обеспечивающих выделение нечетких структур предпочтений по данным, содержащимся в матрицах, формируемых сравниваемыми алгоритмами.
Модуль расчета дескрипторов включает в свой состав комплекс функций, обеспечивающих вычисление весов связей в соответствии с формулой (5), а также значимости объектов в рамках иерархии в соответствии с формулами (6) и (7).
Модуль сравнения дескрипторов обеспечивает расчет расстояния между двумя дескрипторами. В качестве метрики расстояния используется евклидова метрика, расчет расстояния осуществляется согласно (4).
Модуль отображения включает в свой состав комплекс функций, обеспечивающих формирование окон для вывода в них следующей графической информации:
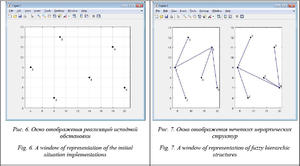
– исходная информация о текущей реализации обстановки;
– нечеткие иерархические структуры предпочтений для текущей реализации обстановки;
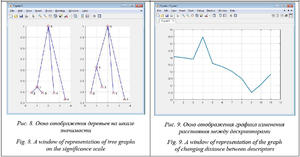
– деревья на шкале значимости, соответству- ющие выявленным нечетким структурам предпочтений;
– график изменения расстояния между двумя дескрипторами за эксперимент в системе коорди- нат rd – №, где rd – расстояние между двумя дескрипторами, № – номер реализации текущей обстановки.
Примеры отображаемой графической информации при сравнении результатов, формируемых двумя алгоритмами агрегирования, приведены на рисунках 6–9.
Сравниваемые алгоритмы различаются между собой параметрами реализуемой гипотезы о предварительном разбиении множества объектов. Алгоритм 1 при расчете функций принадлежности использует так называемые индивидуальные внешние расстояния для каждого объекта, алгоритм 2 – единое внешнее расстояние для всех объектов [5].
Таким образом, изложенный подход обеспечивает формирование сравнительных оценок результатов, получаемых различными алгоритмами агрегирования, путем вычисления расстояния между формируемыми в ходе их работы нечеткими отношениями предпочтения. Расстояние вычисляется с использованием евклидовой метрики между двумя точками, каждая из которых представляет собой отображение формируемого соответствующим алгоритмом бинарного отношения предпочтения в многомерное пространство. Координаты точки отражают значимость соответствующих объектов в индуцируемой отношением предпочтения иерархической структуре на исходном множестве. Это обеспечивает чувствительность используемого показателя к различию результатов работы сравниваемых алгоритмов, представленных в нечеткой форме.
Предлагаемый подход к сравнительной оценке алгоритмов агрегирования и реализующий его программный инструментарий могут использоваться при обосновании выбора рационального варианта алгоритма агрегирования из множества существующих для заданных условий решения информационной задачи в системе сбора и обработки. В этом случае используемый в подходе показатель расстояния может выступать как характеристика функционального качества либо совместно с показателем потребных ресурсов как составной показатель эффективности варианта алгоритма при сравнении его с эталонным вариантом. С помощью данного показателя множество исследуемых вариантов алгоритма можно сравнить с эталонным вариантом как по разовым реализациям развития обстановки, так и по результатам ее развития за эксперимент.
Литература
1. Новоселов П.В., Семенов С.А., Пильщиков Д.Е. Метод формирования траекторий групп воздушных объектов // Радиотехника. 2005. № 5. С. 116–119.
2. Кореньков В.М., Моисеенко П.Г., Семенов С.А. Время нового подхода. URL: http://www.vko.ru/koncepcii/vremya-novogo-podhoda (дата обращения: 06.11.17).
3. Бреслер И.Б., Кореньков В.М., Семенов С.А., Пильщиков Д.Е. Подход к агрегированию данных о высокодинамичных групповых объектах в информационной системе с ограниченными возможностями // Вестн. Тверского гос. ун-та: Сер. Прикладная математика. 2006. Вып. 4. С. 168–179.
4. Бреслер И.Б., Семенов С.А., Тихомиров В.А. Принципы построения нечеткой модели отображения воздушной обстановки в информационных системах реального масштаба времени // Вестн. Тверского гос. ун-та: Сер. Прикладная математика. 2007. Вып. 5. С. 79–86.
5. Тихомиров В.А., Бреслер И.Б., Корниенко В.В., Семенов С.А., Фомин М.Д. Агрегирование информации о воздушной обстановке. Тверь: Изд-во ВА ВКО, 2008. 136 с.
6. Конышева Л.К., Назаров Д.М. Основы теории нечетких множеств. СПб: Питер, 2011. 192 с.
7. Яхъяева Г.Э. Нечеткие множества и нейронные сети. М.: Интернет-Университет Информационных Технологий: БИНОМ, 2006. 316 с.
8. Рыбин В.В. Основы теории нечетких множеств и нечеткой логики. М.: Изд-во МАИ, 2007. 96 с.
9. Вятченин Д.А. Нечеткие методы автоматической классификации. Мн: Технопринт, 2004. 219 с.
10. Харрари Ф. Теория графов; [пер. с англ.]. M.: Едиториал, 2003. 296 с.
11. Чабан Л.Н. Теория и алгоритмы распознавания образов. М.: Изд-во МИИГАиК, 2004. 70 с.
12. Леоненков А.В. Нечеткое моделирование в среде MATLAB и fuzzyTECH. СПб: БХВ-Петербург, 2005. 736 с.



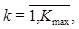 lim Kmax = = card X, и их представление потребителю.
lim Kmax = = card X, и их представление потребителю.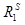 и
и 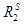 – отношения предпочтения на множестве X, построенные алгоритмами агрегирования A1 и A2, то есть
– отношения предпочтения на множестве X, построенные алгоритмами агрегирования A1 и A2, то есть 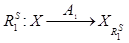 ,
,  Каждое отношение как результат работы алгоритма представлено соответствующей матрицей, то есть
Каждое отношение как результат работы алгоритма представлено соответствующей матрицей, то есть 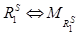 ,
, 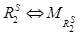 .
.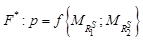 , (1)
, (1)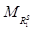 и
и  обладают определенной избыточностью, так как для каждого объекта x Î X существует N альтернатив, где N = card X. В соответствии с теоремой о декомпозиции [6–9], любое нечеткое отношение предпочтения RS, построенное на множестве X, индуцирует его иерархическую структуру, иными словами – стратификацию всех нечетких подмножеств. Исходя из этого такому отношению соответствует
обладают определенной избыточностью, так как для каждого объекта x Î X существует N альтернатив, где N = card X. В соответствии с теоремой о декомпозиции [6–9], любое нечеткое отношение предпочтения RS, построенное на множестве X, индуцирует его иерархическую структуру, иными словами – стратификацию всех нечетких подмножеств. Исходя из этого такому отношению соответствует 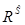 – нечеткое отношение, однозначно отражающее иерархическую структуру множества X на интервале уровня значимости a = [0, 1]. Данное отношение представляет собой нечеткое подмножество множества
– нечеткое отношение, однозначно отражающее иерархическую структуру множества X на интервале уровня значимости a = [0, 1]. Данное отношение представляет собой нечеткое подмножество множества 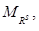 а его элементы в общем случае удовлетворяют условию
а его элементы в общем случае удовлетворяют условию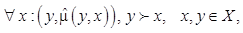
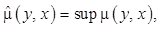 (2)
(2)
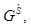 соответствующий полученному отношению, является деревом [10]. Его узлы – элементы множества Х, а дугам соответствуют значения функций принадлежности согласно условию (2) (рис. 1).
соответствующий полученному отношению, является деревом [10]. Его узлы – элементы множества Х, а дугам соответствуют значения функций принадлежности согласно условию (2) (рис. 1).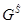 вдоль оси α с привязкой по уровню значимости отношения (рис. 2) каждому элементу множества X может быть поставлена в соответствие характеристика его значимости в заданной структуре предпочтений. Следовательно, при любом A, обеспечивающем построение на множестве Х отношения RS, данное отношение может быть отображено в точку N-мерного пространства отношений, то есть
вдоль оси α с привязкой по уровню значимости отношения (рис. 2) каждому элементу множества X может быть поставлена в соответствие характеристика его значимости в заданной структуре предпочтений. Следовательно, при любом A, обеспечивающем построение на множестве Х отношения RS, данное отношение может быть отображено в точку N-мерного пространства отношений, то есть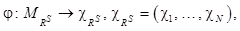

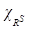 пространства отно- шений будет определяться суммой N ортогональных векторов, каждый из которых характеризует собой значимость соответствующего элемента x в нечеткой структуре предпочтений на множестве X, заданных отношением RS. В свою очередь, по-казателем различия отношений
пространства отно- шений будет определяться суммой N ортогональных векторов, каждый из которых характеризует собой значимость соответствующего элемента x в нечеткой структуре предпочтений на множестве X, заданных отношением RS. В свою очередь, по-казателем различия отношений  . (4)
. (4)
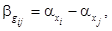 (5)
(5)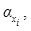
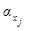 – уровни значимости, при которых элементы xi и xj, инцидентные дуге gij, становятся носителями отношения.
– уровни значимости, при которых элементы xi и xj, инцидентные дуге gij, становятся носителями отношения.
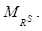
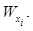 При этом будем учитывать то обстоятельство, что значимость элемента x определяется его местом в выявленной нечеткой иерархической структуре.
При этом будем учитывать то обстоятельство, что значимость элемента x определяется его местом в выявленной нечеткой иерархической структуре.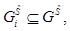 определим как
определим как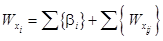 , (6)
, (6)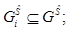
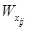 – значимость элемента xj, инцидентного корню xi поддерева
– значимость элемента xj, инцидентного корню xi поддерева 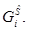
 не имеют исходящих дуг [10]. Для соответствующих им элементов будем полагать
не имеют исходящих дуг [10]. Для соответствующих им элементов будем полагать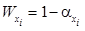 , (7)
, (7)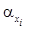 – минимальный уровень значимости, при котором элемент xi является носителем отноше- ния (рис. 4).
– минимальный уровень значимости, при котором элемент xi является носителем отноше- ния (рис. 4).
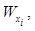 отражающее значимость элемента xi в заданной на множестве X нечеткой структуре предпочтений. На этой основе и выполняется отображение отношения RS в точку пространства отношений
отражающее значимость элемента xi в заданной на множестве X нечеткой структуре предпочтений. На этой основе и выполняется отображение отношения RS в точку пространства отношений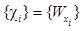 , (8)
, (8)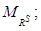
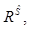 характеризующего нечеткую структуру предпочтений на множестве Х;
характеризующего нечеткую структуру предпочтений на множестве Х;


