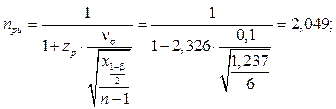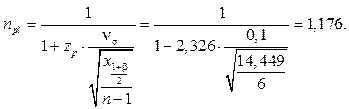Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Исследование распределения коэффициента вариации в задачах статистического анализа испытаний
Аннотация:Рассматривается решение задачи точного распределения коэффициента вариации, статистической характеристики, применяемой при анализе измерений случайных величин, колебаний технологических процессов производства материалов, полуфабрикатов, деталей машин и элементов конструкций, а также при изучении рассеяния характеристик механических свойств, особенно при переменных нагрузках. Важность коэффициента вариации определяется также тем обстоятельством, что он является одним из расчетных параметров при обосновании надежности, долговечности и ресурса, от надежного определения которого в значительной степени зависит безопасная работа машин и конструкций. Точное распределение коэффициента вариации для нормальной совокупности получено на основании известной теоремы о функции распределения отношения двух случайных величин, в данном случае – выборочного среднеквадратического отклонения, имеющего распределение хи-квадрат, и выборочного среднего с нормальным законом распределения. Полученные точные формулы для распределения коэффициента вариации проверялись многократным статистическим моделированием методом Монте-Карло, подтвердившим точность аналитических расчетов. С целью упрощения практических расчетов рассмотрена приближенная модель, показавшая погрешность не более 1,5 % при объемах наблюдений от 3 до 20. Рассмотрены примеры оценки доверительных границ, вероятности безотказной работы и других задач надежности на основании полученных решений.
Abstract:The paper considers the problem of exact distribution of the variation coefficient, the statistical characteristic used for analyzing random variable measurements, the fluctuations in technological processes for production of materials, semi-finished products, machine parts and structural elements, as well as for studying scattering of mechanical properties, es-pecially under variable loads. The importance of the variation coefficient is also determined by the fact that it is one of the design parameters for justification of reliability, durability and life. Safe operation of machines and structures largely depends from the reliable determination of this coefficient. The exact distribution of the variation coefficient for normal population is obtained based on the well-known theorem on the distribution function of the ratio of two random variables. In this case, it is a sample mean square deviation having the chi-square distribution and the sample mean with the normal distribution law. The obtained exact formulas for the variation coefficient distribution were verified by multiple statistical modeling by the Monte Carlo method, which has confirmed the accuracy of analytical calculations. In order to simplify practical calculations, the authors consider an approximate model that has shown an error of no more than 1,5 % for observational volumes from 3 to 20. The paper considers the estimation examples of confidence limits, failure-free operation probability and other reliability problems based on the obtained solutions.
| Авторы: Агамиров Л.В. (mmk@mati.ru) - Национальный исследовательский университет «Московский энергетический институт» (профессор), Москва, Россия, доктор технических наук, Агамиров В.Л. (avl095@mail.ru) - Московский авиационный институт (национальный исследовательский университет) (аналитик), Москва, Россия, кандидат технических наук, Вестяк В.А. (kaf311@mai.ru) - Московский авиационный институт (национальный исследовательский университет) (зав. кафедрой), Москва, Россия, доктор физико-математических наук | |
| Ключевые слова: рассеяние характеристик, распределение, механические испытания, испытания на усталость, надежность, расчет на прочность, обработка наблюдений, долговечность, выносливость, ресурс, коэффициент вариации |
|
| Keywords: scattering of characteristics, distribution, mechanical testing, fatigue test, reliability, strength calculation, observations processing, durability, endurance, life, variation coefficient |
|
| Количество просмотров: 7213 |
Статья в формате PDF Выпуск в формате PDF (29.74Мб) |
Коэффициент вариации используется в задачах обработки наблюдений для оценки однородности выборок, сравнения разброса случайных параметров, имеющих различные размерности, исследования регрессионных зависимостей, характеризующихся изменениями выборочных дисперсий в связи с вариациями факторов эксперимента, и во многих других задачах. При определении характеристик механических свойств материалов коэффициент вариации вычисляется с целью оценки колебаний технологии в производственном процессе или сравнения технологических процессов производства материалов и полуфабрикатов на разных предприятиях [1–5]. В задачах исследования характеристик сопротивления усталостному разрушению при цикли- ческих испытаниях материалов и элементов конструкций вычисляют коэффициент вариации логарифма долговечности, который служит показателем изменчивости рассеивания характеристик усталостных свойств, в связи с вариацией средних значений долговечностей при испытаниях. Коэффициент вариации предела выносливости входит как параметр во многие модели расчетно-экспериментальной оценки выносливости деталей машин и натурных элементов конструкции. При вероят- ностном расчете в условиях регулярной переменной нагруженности коэффициенты вариации действующей амплитуды и предела выносливости определяют вероятность безотказной работы для случая нормального распределения указанных напряжений [6–9]. Таким образом, коэффициенты вариации характеристик статической и циклической прочности являются важными расчетными показателями долговечности, выносливости и ресурса, от надежного определения которых в значительной степени зависит безопасная работа машин и конструкций. В то же время коэффициент вариации является величиной случайной, имеющей вероятностное распределение. Это обстоятельство обусловливает необходимость изучения этого распределения с целью выбора в качестве расчетной характеристики не медианного значения коэффициента вариации, а значения, соответствующего некоторой наперед заданной (доверительной) вероятности. Очевидно, что выбор верхней границы распределения ко- эффициентов вариации существенно снижает ве- роятность безотказной работы и увеличивает ожидаемое рассеяние характеристик циклической долговечности, что отражается на величине гарантированного ресурса элемента конструкции. В работе [10] применительно к вероятностным задачам в расчетах прочности самолетов и уточнения распределения разрушающих нагрузок рассматривается методика оценивания коэффициента вариации при малых объемах наблюдений, основанная на функции распределения выборочного коэффициента вариации. Там же приведен пример вычисления поправок к определению расчетного коэффициента вариации. Отмечается, что использование приближенных соотношений, основанных на выборочных моментах распределения, для построения асимптотически нормальных доверительных границ возможно лишь при больших объемах наблюдений (не менее 100 объектов), что нереально в условиях механических испытаний дорогостоящих материалов и элементов конструкций. В расчетной практике встречается целый класс случайных величин, для которых физически обосновано применение вполне конкретных законов распределения в связи с природой рассеяния случайных величин. Известно, что распределение большинства характеристик статических и циклических свойств материалов гипотетически подчиняется нормальному или логарифмически нормальному закону распределения в силу примерно эквивалентного влияния на эти характеристики большого числа факторов, связанных со структурной неоднородностью материалов, случайными колебаниями технологических процессов их формообразования, режимов последующей механической и термической обработки. Целью настоящей работы является изучение распределения коэффициента вариации в задачах механических испытаний конструкционных материалов, природа случайного рассеяния свойств которых связана, главным образом, с их структурной неоднородностью, а также деталей машин и элементов конструкций, распределение характеристик прочности и надежности которых имеет дополнительную вариативность за счет случайных колебаний в режимах технологии, размеров и форм деталей. Точное распределение коэффициента вариации может быть получено на основании функции распределения отношения двух независимых случайных величин [11]. Применительно к коэффициенту вариации g = d/a рассмотрим точное решение для нормального закона распределения. В этом случае плотность распределения числителя есть распределение стандартного отклонения в нормальной выборке (
и функцией распределения:
где стандартная функция плотности распределения c2 с f степенями свободы имеет вид
Распределение знаменателя (то есть выборочное среднее) подчиняется нормальному закону N(a, d) с параметрами (a,
После преобразований и замены переменных окончательные формулы для функции распределения выборочного коэффициента вариации
или
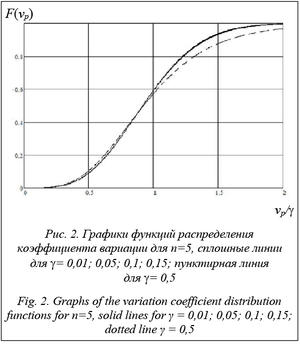
В формулах (6) и (7) g – генеральное значение коэффициента вариации. Для удобства графического представления и сопоставления результатов расчеты функций распределения представлены на рисунках 1 и 2 для величины отношения v/g выбо- рочного коэффициента вариации к генеральному значению (то есть по оси x откладывается отношение v/g). Распределение коэффициента вариации существенно зависит от объема выборки (на рис. 1 n = 5, 10, 20 при g = 0,3). На рисунке 2 представлены аналогичные графики функции распределения коэффициента вариации, но при фиксированном объеме выборки n=5 для разных значений g = 0,01, 0,05, 0,1, 0,15 и 0,5. На рисунке 2 график функции распределения коэффициента вариации практически не зависит от генерального значения коэффициента вариации, по крайней мере, в практически важном для технических задач диапазоне g = 0,01–0,15. Для первых четырех значений коэффициента вариации графики функции распределения практически сливаются в одну кривую, то есть можно считать, что распре- деление не зависит от генерального значения ко- эффициента вариации. Это позволило получить упрощенную формулу для распределения коэффициента вариации, весьма близкую к точному распределению. Формула учитывает слабое влияние второго сомножителя подынтегральной функции (6), (7) и поэтому основывается только на распределении выборочного стандартного отклонения:
Таким образом, квантиль распределения коэффициента вариации vp определяется путем следующего простого преобразования квантиля распреде- ления c2 (xp):
На рисунке 2 видно, что кривая распределения практически сливается с графиками точных функций для вышеуказанного диапазона ожидаемых значений коэффициента вариации. В таблице представлены расчеты распределения относительных коэффициентов вариации для объемов выборки от 3 до 20, выполненные по точным формулам (6), (7) и по приближенной формуле (9) (выделено жирным шрифтом). В таблице показано, что значения расчетной относительной погрешности определения коэффициента вариации по формулам (6) и (7) и по формуле (9) близки. Алгоритм точного вычисления обратной функции распределения коэффициента вариации методом Нэлдера–Мида (деформируемого многогран- ника) изображен на рисунке 3 (см. также [12]). Программа на языке Javascript размещена по адресу http://inteh.mpei.ru/programs/Stat/stat.html в открытом доступе. На рисунке 3 в качестве исходных данных задаются значения ожидаемого коэффициента вариации (gamma), объема испытаний (n), относительной точности расчета (eps), максимального количества итераций (itmax), заданного уровня вероятности (beta).
Начальное приближение для квантиля коэффициента вариации рассчитывается по формуле (9). Затем в итерационной функции метода деформируемого многогранника simplex вычисляется значение минимизируемой функции funx, представляющей собой квадрат разности между расчетной и заданной вероятностями. Численное интегрирование по формуле (6) для примера производится методом Симпсона в функциях simpson и fsimpson. Итерационная процедура продолжается до достижения заданной относительной точности eps. Расчеты показывают весьма высокую устойчивость и точность расчетов в широком диапазоне значений коэффициентов вариации и объемов испытаний, что нетрудно проверить в пользовательской программе по вышеуказанному адресу. Программа статистического моделирования распределения коэффициента вариации методом Монте-Карло на языке JavaScript размещена по адресу http://www.swsys.ru/uploaded/image/2018_1/ 2018-1-dop/1.jpg. Программа может быть легко адаптирована для получения распределения коэффициента вариации в случае отличных от нормального типов распределений, для которых точные решения неизвестны, а приближенные модели недостаточно точны. Для этого можно только заменить одну функцию z=invnormaldistribution(z) обратного нормального распределения на соответствующую функцию распределения, отличного от нормального. Программа является простой, полностью рабочей, содержит необходимые комментарии и поэтому не требует отдельного описания. Пример 1. В результате усталостных испытаний 10 образцов из алюминиевого сплава на изгиб с вращением получены оценки среднего значения, среднего квадратичного отклонения и коэффициента вариации логарифма долговечности: Необходимо произвести оценку двусторонних 95 % доверительных границ для коэффициента вариации логарифма долговечности. Расчеты по формуле (9) дают следующие результаты:
Таким образом, с вероятностью 95 % указанный интервал (0,0193–0,0511) накрывает истинное значение коэффициента вариации. Пример 2. Определить вероятность безотказ- ной работы элемента конструкции при симметрич- ном цикле (вероятность неразрушения до базовой долговечности) при действии амплитуды переменных напряжений sa = 90 мПа. Оценка коэффициента вариации действующих амплитуд составляет
При подстановке в уравнение верхних 97,5 % доверительных границ коэффициентов вариации по формуле (9) расчетные значения изменятся следующим образом:
Пример 3. В результате статических испытаний 7 кронштейнов крепления крыла самолета получена оценка коэффициента вариации разрушающего напряжения vs = 0,1. Произвести оценку двусторонних b = 95 % доверительных границ для коэффициента снижения разрушающего напряжения в связи с рассеянием свойств, соответствующего нижней квантили распределения разрушающего напряжения уровня P = 0,01 в предположении его нормального распределения. Определим оценку коэффициента снижения разрушающего напряжения как отношение оценок среднего значения разрушающего напряжения
где оценка квантиля разрушающего напряжения в соответствии с нормальным законом определяется из уравнения В соответствии с уравнением (9) верхняя и нижняя доверительные границы коэффициента снижения разрушающего напряжения в связи с рассеянием свойств определяются по формулам:
Выводы Таким образом, в статье обоснована необходимость исследования распределения коэффициента вариации как важного относительного показателя рассеяния случайных величин и изменчивости случайных процессов в задачах, возникающих при анализе результатов механических испытаний, расчетах надежности и ресурса машин и элементов авиационных конструкций при малых объемах выборочных совокупностей, характерных для практики. Кроме того, получены точные функции распределения коэффициента вариации для гипотетического нормального закона распределения случайной величины, позволяющие производить необходимые расчеты в указанном диапазоне объемов наблюдений. На основании анализа точных функций распределения разработана приближенная модель для расчета функции распределения коэффициента вариации, имеющая погрешность не более 1,5 % в диапазоне объемов наблюдений n = 3–20. Для точных расчетов обратной функции распределения коэффициента вариации разработаны алгоритм и пользовательская программа, основанные на методе деформируемого многогранника. Для отличных от нормального закона типов распределений предлагаются алгоритм и программа статистического моделирования методом Монте-Карло. Литература 1. Агамиров Л.В. Методы статистического анализа механических испытаний. М.: Интермет Инжиниринг, 2004. 127 с. 2. Степнов М.Н. Статистические методы обработки результатов механических испытаний. М.: Машиностроение, 2005. 399 с. 3. Пугачев В.С. Теория вероятностей и математическая статистика. М.: Физматлит, 2002. 496 с. 4. Воробьев А.З., Олькин Б.И., Стебенев В.Н., Родчен- ко Т.С. Сопротивление усталости элементов конструкций. М.: Машиностроение, 1990. 240 с. 5. Райхер В.Л. Рассеяние усталостной долговечности. М.: Изд-во ЛАТМЭС, 2003. 144 с. 6. Бойко Т.С. Методика расчета интегральной повторяемости воздушных порывов, действующих на самолет в типовом полете // Авиационно-космическая техника и технология. 2016. № 2. С. 42–48. 7. Фомичев П.А., Клепцов В.И. Обоснование долговечности конструкции транспортного самолета при многоцелевом применении по результатам ресурсных и летных испытаний // Вестн. СГАУ. 2013. № 2. С. 46–52. 8. Когаев В.П. Расчеты на прочность при напряжениях, переменных во времени. М.: Машиностроение, 1993. 363 с. 9. Райхер В.Л. Усталостная повреждаемость. М.: Изд-во МАТИ, 2006. С. 238. 10. Селихов А.Ф., Чижов В.М. Вероятностные методы в расчетах прочности самолета. М.: Машиностроение, 1987. 240 с. 11. Гнеденко Б.В. Курс теории вероятностей. М.: Едиториал УРСС, 2005. 448 с. 12. Агамиров Л.В., Агамиров В.Л., Вестяк В.А. Метод расчета квантилей распределения характеристик усталостных свойств элементов конструкций // Вестн. МАИ. 2011. Т. 18. № 4. С. 71–76. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=4417 |
Версия для печати Выпуск в формате PDF (29.74Мб) |
| Статья опубликована в выпуске журнала № 1 за 2018 год. [ на стр. 166-171 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Фазовый переход наработки на отказ в растущих вычислительных сетях
- Методы сокращения количества уязвимостей в специальном программном обеспечении реального времени
- Алгоритмы планирования усталостных испытаний авиационных материалов
- Методы упреждающего прогнозирования состояния широкополосной сети связи
- Надежность тренажерных систем, построенных на двухранговых локальных вычислительных сетях
Назад, к списку статей



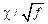 ), то есть основано на распределении Пирсона c2 с функцией плотности:
), то есть основано на распределении Пирсона c2 с функцией плотности: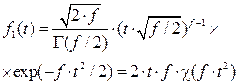 (1)
(1)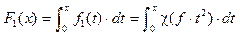 , (2)
, (2)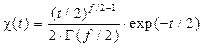 . (3)
. (3)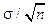 ). Функция плотности и функция распределения нормального закона имеют следующий вид:
). Функция плотности и функция распределения нормального закона имеют следующий вид: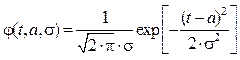 , (4)
, (4)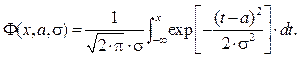 (5)
(5) в случае нормального закона распределения приобретают следующий вид:
в случае нормального закона распределения приобретают следующий вид: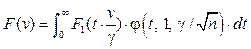 (6)
(6)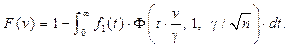 (7)
(7)
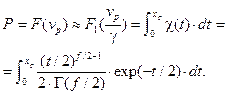 (8)
(8)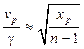 . (9)
. (9)

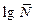 = = 6,983;
= = 6,983; 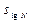 = 0,194;
= 0,194;  = 0,028.
= 0,028.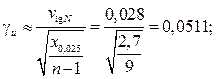
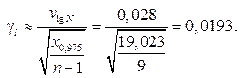
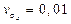 при объеме выборки n1 = 7. Предел выносливости при симметричном цикле для указанной базы составляет s-1 = 100 мПа. Оценка коэффициента вариации предела выносливости составляет
при объеме выборки n1 = 7. Предел выносливости при симметричном цикле для указанной базы составляет s-1 = 100 мПа. Оценка коэффициента вариации предела выносливости составляет 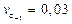 при объеме выборки n2 = 10. Нормативное значение вероятности безотказной работы – 0,999. Примем нормальным закон распределения предельных и действующих амплитуд переменных напряжений. Квантиль нормированного нормального закона распределения [6], определяющий вероятность безотказной работы R, вычисляется по уравнению
при объеме выборки n2 = 10. Нормативное значение вероятности безотказной работы – 0,999. Примем нормальным закон распределения предельных и действующих амплитуд переменных напряжений. Квантиль нормированного нормального закона распределения [6], определяющий вероятность безотказной работы R, вычисляется по уравнению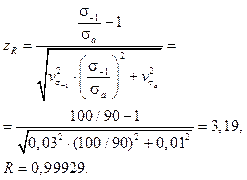
 то есть вероятность безотказной работы становится существенно меньше заданного нормативного значения.
то есть вероятность безотказной работы становится существенно меньше заданного нормативного значения.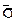 к нижнему квантильному значению sp для вероятности P:
к нижнему квантильному значению sp для вероятности P: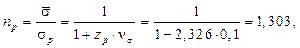
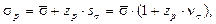 zp – квантиль нормированного нормального закона (z0,01 = –2,326), vs – оценка коэффициента вариации разрушающего напряжения.
zp – квантиль нормированного нормального закона (z0,01 = –2,326), vs – оценка коэффициента вариации разрушающего напряжения.