В практике компьютерного моделирования поведения сложных систем часто проявляется феномен скачкообразного и лавинообразного изменения характеристик поведения системы под воздействием плавных изменений одного или нескольких ключевых параметров. Так, при исследовании распространения массовых эпидемий относительно малые изменения значений одного или нескольких параметров (например, вероятности инфицирования) могут привести к скачкообразному изменению поведения всей системы (заболевание локального характера становится широкомасштабным). Одним из интересных и эффективных инструментов исследования подобных ситуаций является метод построения и анализа роста перколяционных кластеров.
Теория перколяции достаточно подробно описывает процессы на виртуальных решетках, по отношению к ним доказан ряд строгих утверждений. Для реализации широкомасштабных приложений подобных процессов эффективно используются возможности современных суперкомпьютерных технологий. Что, в свою очередь, требует разработки соответствующих моделей компьютерной имитации, в том числе мультиагентных [1–3], а также специализированных алгоритмов распараллеливания [4, 5].
Агентный подход в разработке имитационных моделей применяется во всех случаях, когда именно индивидуальное поведение объектов является существенным в системе, а интегральные характеристики и динамика всей системы выводятся из этих особенностей. Под агентом понимается некая сущность, которая обладает активностью, автономным поведением, может принимать решения в соответствии с определенными правилами, взаимодействовать с окружением и другими агентами, а также изменяться (эволюционировать) [6–8]. Агентные модели используются для исследования децентрализованных систем, динамика функционирования которых определяется не глобальными правилами и законами, а наоборот, эти глобальные правила и законы являются результатами индивидуальной активности агента или группы агентов. Цель агентной модели – получить представление об этих глобальных правилах, исходя из предположений об индивидуальном, частном поведении ее активных объектов и взаимодействии этих объектов в системе.
При создании агентной модели логика поведения агентов и их взаимодействие не всегда могут быть выражены чисто графическими средствами, часто приходится использовать программный код. Обычно для этих целей применяется язык Java.
С применением положений теории перколяции в МСЦ РАН – филиале ФНЦ НИИСИ РАН был разработан действующий прототип реализации алгоритма многократной маркировки перколяционных кластеров (ММПК) Хошэна–Копельмана [9] на языке Си с использованием библиотеки MPI. Он позволяет выделить связные подграфы (кластеры) некоторого графа (решетки), а также выяснить, к какому кластеру относится тот или иной узел решетки. Алгоритм был адаптирован для применения на многопроцессорной системе. Данный вариант алгоритма совпадает с однопроцессорным вариантом за одним исключением: вместо прохода по всей решетке каждый процессор активизирует действия алгоритма ММК только на выделенной ему группе узлов с последующим обменом информацией между процессорами.
Разработанный прототип был использован для исследования возникновения и распространения широкомасштабных эпидемий. Для формирования анализируемой решетки использовались общедоступные демографические данные о численности населения городов всего мира и некоторые предположения об интенсивности и характере взаимодействия между людьми. Для получения сведений о численности населения городов был разработан алгоритм обработки и анализа карт плотности населения (реализация на языке java). Сами карты были позаимствованы у Google при помощи Google Maps API, а для удобства восприятия результатов имитационных экспериментов были разработаны соответствующие средства визуализации.
Принципиальная схема действующего прототипа
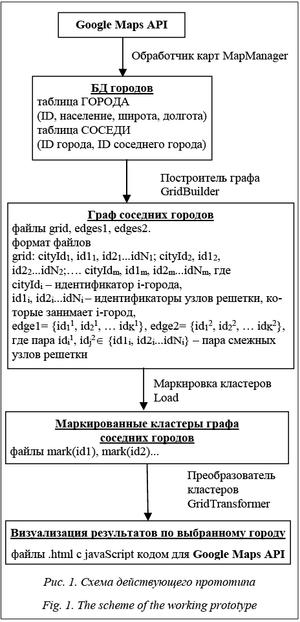 Действующий прототип реализации алгоритма многократной маркировки перколяционных кластеров Хошэна–Копельмана, разработанный в МСЦ РАН, состоит из этапов, представленных на рисунке 1.
Действующий прототип реализации алгоритма многократной маркировки перколяционных кластеров Хошэна–Копельмана, разработанный в МСЦ РАН, состоит из этапов, представленных на рисунке 1.
При помощи алгоритма сбора информации о численности населения (обработчик карт Map- Manager) были получены данные о городах мира и сохранены в БД в формате «номер города, численность населения, широта, долгота». БД городов содержит информацию о 56 976 городах с общей численностью населения 6 114 628 510 человек.
С помощью алгоритма формирования решетки взаимодействия представителей популяции (построитель графа GridBuilder) была создана исходная решетка (реализация на java) и сохранена в трех файлах: решетка grid размера 475 Мб и 2 файла edges1 и edges2 – ребра общим размером 429 Мб. Для каждого значения входного изменяемого параметра вероятности заражения при контакте с больным (параметр p = 0,01–1,00 с шагом 0,01) исходной решетки в оперативной памяти формируется анализируемая решетка.
Далее проводилась разбивка графа соседних го- родов на связанные подмножества алгоритмом Хошена–Копельмана (маркировка кластеров Load). Для каждой анализируемой решетки запускался алгоритм ММК. Работу алгоритма можно разделить на три этапа.
Этап. 1. Инициализация: первый процесс загружает решетку в оперативную память из файла, преобразует ее по входным параметрам, распределяет узлы в группы по процессам и отсылает им. Остальные процессы ждут получения своей группы узлов. Получив такую группу, процессы выделяют из них подгруппу внешне связанных узлов, то есть узлов, связанных с узлами из групп других процессов. Для каждого узла своей группы задаются начальные значения меток в соответствии с абсолютным (в рамках всей решетки) номером узла. Каждый процесс создает группу внешних уз- лов, связанных с узлами своей группы, и инициализирует их метками связанных узлов своей группы.
Этап 2. Работа собственно алгоритма. Каждый процесс запускает алгоритм ММК на своей группе узлов.
Этап 3. Обмен информацией. Происходит в несколько шагов до тех пор, пока после очередного обмена метки узлов всех процессов не перестанут изменяться. Обмен информацией можно разделить на три шага. Первый шаг – каждый процесс посылает значения меток узлов из подгруппы внешне связанных узлов тем процессам, с которыми эти узлы связаны. Второй шаг – каждый процесс принимает значения меток от процессов, имеющих узлы, связанные с узлами данного. Эти значения присваиваются меткам узлов из группы внешних узлов. Если хоть одна из меток узлов из внешней группы была изменена, процесс должен повторить обмен информацией. Все метки узлов своей группы, равные замененным меткам внешней группы, должны быть также заменены. Третий шаг – отправка сообщения первому процессу о том, должен или нет данный процесс повторить обмен информацией с другими процессами. Первый процесс получает от всех процессов подобную информацию. Если все процессы не нуждаются в повторном обмене, первый процесс рассылает всем остальным сигнал о завершении работы всего алгоритма и начинает процедуру сбора данных по меткам их узлов. Если же хоть один процесс прислал сообщение, что ему необходимо продолжить обмен, всем процессам придется повторить процедуру обмена информацией.
В качестве результата маркировки кластеров был получен массив кластерных меток (с индексами от 1 до 100). Размер каждого сохраненного массива составляет около 24 Мб.
Программа маркировки кластеров Load запускалась в Межведомственном суперкомпьютерном центре на суперкомпьютере МВС-100К с общим количеством процессорных ядер 13 004 на 48 264 процессорах. Среднее время выполнения программы с входным параметром p от 0,01 до 1 с шагом в 0,01 при постоянных значениях t = 1, 3, 5, 10, 15, 20, 25, 30 дней составило около 10 минут для каждого значения t [10].
На суперкомпьютере МВС-10П с общим количеством процессорных ядер 28 704 среднее время выполнения этой программы составило около 5 минут.
На следующем этапе проводился имитационный эксперимент с определенным городом (преобразователь кластеров GridTransformer). Визуализация полученных результатов в модели проводится с помощью Google Maps Api (реализация на java).
Выбирался город – очаг заражения, задавалось количество зараженных узлов в этом городе, и для данных p и t загружался вычисленный ранее массив кластерных меток. После определения меток зараженных узлов выбранного города проводился последовательный обход меток всех узлов из загруженного массива. Если метка являлась потенциально зараженной, то город, в который входил узел с данной меткой, также объявлялся потенциально зараженным. Таким образом формировался список потенциально зараженных городов. Этот список сохранялся в виде JavaScript-команд Google Maps API в html-файле. В зависимости от численности населения зараженный город помечался красным кругом определенного размера. Для визуализации результатов html-файл запускался в браузере.
Результаты моделирования попыток предсказания распространения массовых эпидемий
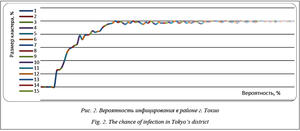
На рисунке 2 демонстрируется результат проведения численного эксперимента при размеще- нии очага заражения в г. Токио, который является ближайшим крупным населенным пунктом к возможным местам вскрытия и расконсервации за- хоронений бактериологических отходов (под воздействием тектонических разломов, резкого потеп- ления, террористических актов, промышленных аварий и т.д.).
Как видно, максимальная вероятность инфицирования в районе Токио достигает ~ 0.3, то есть уже при вероятности инфицирования 0.3 эпидемия за счет высокой плотности населения в регионе может превратиться в широкомасштабную пандемию.
На рисунке 3 продемонстрированы результаты имитационных экспериментов при возникновении очага заражения в районе г. Токио.

В период с 5-го по 7-й день виден резкий скачок размера потенциально зараженного кластера и эпидемия имеет все шансы распространиться по миру.
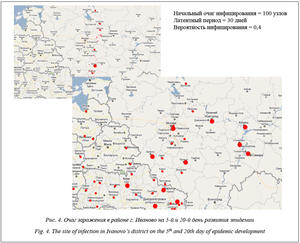
Проводились численные эксперименты и с размещением очага заражения в городах России. На рисунке 4 продемонстрированы результаты имитационных экспериментов при возникновении очага заражения в районе г. Иваново. Результаты показывают, что даже при более высокой вероятности инфицирования и более длительном периоде, чем в Токио, эпидемия в стадию пандемии не переходит.
Расчеты проводились в Межведомственном суперкомпьютерном центре Российской академии наук на высокопроизводительных вычислительных системах МВС-100К и МВС-10П.
Работа выполнена в МСЦ РАН в рамках государственного задания по теме «Разработка архитектур, системных решений и методов для создания вычислительных комплексов и распределенных сред мультипетафлопсного диапазона производительности, в том числе нетрадиционных архитектур микропроцессоров» (№ 0065-2018-0409).
Литература
1. Калихман Р.С., Шебеко Ю.А. Моделирование роста перколяционных кластеров на компьютерах с сильно выраженной параллельной архитектурой // Вычислительные технологии: сб. науч. тр. СО РАН. 1995. Т. 4. № 10. 344 с.
2. Кондратьев М.А., Ивановский Р.И., Цыбалова Л.М. Применение агентного подхода к имитационному моделированию процесса распространения заболевания // Науч.-технич. ведомости СПбГУ. 2010. Т. 2. № 2. С. 189–195.
3. Тарасевич Ю.Ю. Перколяция: теория, приложения, алгоритмы. М.: УРСС, 2002. 64 c.
4. Korneev V., Semenov D., Kiselev A., Shabanov B., Tele- gin P. Multiagent distributed Grid scheduler. Proc. Federated Conf. on Comp. Sc. and Inform. Syst., 2011, pp. 577–580.
5. Телегин П.Н. Настройка выполнения параллельных про-
грамм // Программные продукты и системы. 2012. № 4. С. 25–30.
6. Карпов Ю.Г. Имитационное моделирование систем. Введение в моделирование с AnyLogic 5. СПб: БХВ-Петербург. 2005. 400 с.
7. Утакаева И.Х. Имитационное моделирование распространения эпидемий на основе агентного подхода // Науч. журн. КубГАУ. 2016. № 121. URL: http://ej.kubagro.ru/2016/07/pdf/ 85.pdf (дата обращения: 04.03.2018).
8. Боев Б.В. Прогнозно-аналитические модели эпидемий. М., 2005. 10 с.
9. Лапшина С.Ю. Высокопроизводительные вычисления в практике моделирования роста перколяционных кластеров // Программные продукты и системы. 2011. № 4. С. 75–79.
10. Клинов М.С., Лапшина С.Ю., Телегин П.Н., Шабанов Б.М. Особенности использования многоядерных процессоров в научных вычислениях // Вестн. УГАТУ. 2012. Т. 16. № 6. С. 25–31.
References
- Kalikhman R.S., Shebeko Yu.A. Modeling the growth of percolating clusters on computers with a strongly pronounced parallel architecture. Computational Technologies: Proc. SB RAS. 1995, vol. 4, no. 10, 344 p. (in Russ.).
- Kondratev M.A., Ivanovsky R.I., Tsybalova L.M. Application of the agent approach to the simulation of the spread of the disease. Sci. and Tech. Reports of the Peter the Great St. Petersburg Polytechnic Univ. 2010. vol. 2, no. 2, pp. 189–195 (in Russ.).
- Tarasevich Yu.Yu. Percolation: Theory, Applications, Algorithms. Moscow, URSS Publ., 2002, 64 p.
- Korneev V., Semenov D., Kiselev A., Shabanov B., Telegin P. Multiagent Distributed Grid Scheduler. Proc. of the Federated Conf on Computer Science and Information Systems. 2011, pp. 577–580.
- Telegin P.N. Configuring the Execution of Parallel Programs. Software & Systems. 2012, no. 4, pp. 25–30 (in Russ.).
- Karpov Yu.G. System Simulation. Introduction to Modeling with AnyLogic 5. St. Petersburg, BHV-Peterburg Publ., 2005,
400 p.
- Utakaeva I.Kh. Simulation modeling of distribution of epidemics on the basis of agent approach. Scientific J. of KubSAU. 2016, no. 121. Available at: http://ej.kubagro.ru/2016/07/pdf/85.pdf (accessed March 4, 2018).
- Boev B.V. Predictive-Analytical Models of Epidemics. Moscow, 2005, 10 p.
- Lapshina S.Yu. High-performance computing in the practice of modeling the growth of percolating clusters. Software & Systems. 2011, no. 4, pp. 75–79 (in Russ.).
- Klinov M.S., Lapshina S.Yu., Telegin P.N., Shabanov B.M. Features of Using Multi-Core Processors in Scientific Computing. Bulletin of USATU. 2012, vol. 16, no. 6, pp. 25–31 (in Russ.).







