Оптимальное управление с обратной связью одним классом нелинейных систем по квадратичному критерию
| Афанасьев А.П. (apa@isa.ru) - Институт проблем передачи информации им. А.А. Харкевича РАН (ИППИ РАН), Московский государственный университет им. М.В. Ломоносова (профессор), Москва, Россия, доктор физико-математических наук, Дзюба С.М. (sdzyuba@mail.ru) - Тверской государственный технический университет (профессор), Тверь, Россия, доктор физико-математических наук, Пчелинцев А.Н. (pchelintsev.an@yandex.ru) - Тамбовский государственный технический университет (доцент), Тамбов, Россия, кандидат физико-математических наук, Емельянова И.И. (emelyanova-123@yandex.ru) - Тверской государственный технический университет (ст. преподаватель), Тверь, Россия | |
| Ключевые слова: метод последовательных приближений, оптимальное управление с обратной связью, нелинейная система, объектно-ориентированное программирование |
|
| Keywords: successive approximations method, optimal feedback control, nonlinear system, object(oriented programming |
|
|
|
|
Проблема синтеза оптимального управления нелинейными системами с выделенной линейной частью по квадратичному критерию является актуальной. Многие модели технических, физических, биологических и экономических систем описываются именно такими моделями. Для решения исходной задачи в виде закона управления с обратной связью рассмотрим нелинейную динамическую систему, характеризуемую дифференциальным уравнением
где x = (x1, …, xn) – n-мерный действительный вектор состояния; u = (u1, …, um) – m-мерный действительный вектор управления; A и B – действительные (n´n) и (n´m) матрицы; f = (f1, …, fn) – векторная функция, определенная и непрерывная вместе со своими частными производными Предположим, что начальное состояние x(0) = c (2) задано, а задача управления системой (1) заключается в минимизации функционала
в котором T – фиксированное конечное время; Q и P – положительные полуопределенные (n´n) матрицы; R – положительно определенная (m´m) матрица; e(t) = x(t) – z (t) – ошибка системы; z = (z1, …, zn) – заданный режим функционирования. Легко заметить, что непосредственное применение к рассматриваемой задаче принципа максимума Л.С. Понтрягина приводит к достаточно сложной краевой задаче, если только (1)–(3) не сводится к линейно-квадратичной задаче слежения (см., например, [1]). Однако во многих практических ситуациях режим В общем случае для получения решения (или оценки решения) задачи используют самые разные методы (см., например, [2] и [3–9]). Одним из основных здесь является метод последовательных приближений, описанный в [2]. Внешне простой и понятный, он сводит исходную задачу к некоторой последовательности линейно-квадратичных задач. Вместе с тем он до сих пор не получил широкого распространения, поскольку его сходимость не доказана. Последнее, в частности, объясняется тем, что в схеме последовательных приближений оператор системы меняется от итерации к итерации. Цель настоящей работы – получить решение задачи (1)–(3) в виде закона управления с обратной связью. Для получения искомого решения используется процедура, являющаяся модификацией метода [2] и заключающаяся в создании некоей специальным образом генерируемой последовательности вспомогательных линейно-квадратичных задач. Это позволяет в некоторых случаях установить сходимость метода, а из сходимости доказать существование оптимального управления и получить процедуру его построения. Метод построения приближенных решений Формально опишем метод последовательных приближений, на котором будут базироваться все дальнейшие построения. Следуя [9], для всех N = 0, 1, … рассмотрим вспомогательную задачу о минимизации функционала:
с ограничением
где xN и uN – некоторые функции, определенные и непрерывные на отрезке [0, T]. Для фиксированных xN и uN оптимальное управление uN+1(t) в задачах (4) и (5) дается законом управления с обратной связью
в котором xN+1(t) – решение уравнения (5), соответствующее uN+1(t) и удовлетворяющее начальному условию xN+1(0) = c; (7) K(t) – решение матричного дифференциального уравнения Риккати
с граничным условием K(T) = P; (9) hN+1(t) – решение линейного дифференциального уравнения
с граничным условием (см. [1]) hN+1(T) = Pz(T) (11) Таким образом, если начальное приближение x0(t), u0(t) задано, то соотношения (4)–(11) определяют схему последовательных приближений, которая, как будет показано далее, при всех достаточно малых значениях T позволяет установить существование решения задачи (1)–(3) и дает эффективную процедуру построения этого решения. Отметим также, что для простоты начальное приближение здесь будет определено соотношениями x0(t) = c (12) и В [9] показано: если величина Т достаточно мала, то решение задачи (1)–(3) существует и может быть получено сходящимся в данном случае методом последовательных приближений (4)–(13). И наоборот, легко видеть, что в случае сходимости метода последовательных приближений (4)–(13) решение задачи (1)–(3) существует и может быть получено методом (4)–(13) вне зависимости от значения Т. Таким образом, метод (4)–(13) является обоснованным для решения задач во многих практических ситуациях. Далее приведен пример его использования для решения стабилизации режимов работы регулятора Уатта. Иллюстративный пример Рассмотрим систему дифференциальных уравнений j¢ = y,
где a, b, g, b и g – параметры системы, а u1(t) – управление. Система (14) может быть приведена к виду (1) следующим образом:
Для критерия (3)
где E – единичная матрица, а значения T (длина временного отрезка) q1, q2, q3, r и kp считаются задаными. Предположим, что вектор z постоянен и его элементы также заданы. Пусть в формулах (5) и (7) c = kzZ + Dz, Для решения задачи (1)–(3) для заданного значения T разработана компьютерная программа на языке C++, основанная на описанном методе последовательных приближений (5)–(13). Чтобы реализовать его, вначале нужно численно решить матричное уравнение Риккати (8) в обратном направлении по времени (см. граничное условие (9)). Причем оно решается один раз, и массив-сетка матриц (в программе она относится к типу vector) хранится в памяти для дальнейшего использования в схеме последовательных приближений (5)–(13) (см. в [10] строки 222–227). Для эффективной программной реализации алгоритма построения приближений к u1(t) решение уравнений (8), а также (5) и (10) на каждой итерации с точки зрения уменьшения дублирования кода нужно использовать принцип полиморфизма объектно-ориентированного программирования. Суть в том, что численное решение обыкновенных дифференциальных уравнений универсально по форме уравнения – подходит для решения и скалярного, и векторного, и матричного дифференциального уравнений. Такое возможно, если использовать шаблоны классов C++. Также сам численный алгоритм решения уравнения правильнее вынести в отдельный шаблонный класс с чисто виртуальной функцией f(), перекрытие которой в потомке реализует вычисление конкретной правой части системы дифференциальных уравнений. Заметим, что на каждой итерации с номером N+1 сначала численно решается уравнение (10) в обратном времени, так как его правая часть не зависит от xN+1(t). Далее полученная сетка для векторной функции hN+1(t) используется при численном интегрировании уравнения (5) в прямом времени. Представим фрагмент кода (полная программа приведена в [11]), где объявлен универсальный метод численного решения дифференциальных уравнений для задачи (1)–(3) оптимального управления: #ifndef _RK4_H_INCLUDED_ #define _RK4_H_INCLUDED_ #include #include template class rk4 { public: void solve(const double &t0, int n, const TypeSol &x0, std::vector &x, const double &h, int d = 1, bool info = true, std::vector *x_prev_t = NULL, std::vector *u_prev_t = NULL, std::vector *K_t = NULL, std::vector *H_t = NULL, std::vector *u_t = NULL) { x.push_back(x0); TypeSol k1, k2, k3, k4, x_c, x_new; double t = t0, s = d*h, s2 = s/2; TypeSol *x_prev, *u_prev, *H = NULL; Сделаем пояснения: t0 – значение начального момента времени (в данном случае оно может быть равно или 0, или T); n – количество шагов численного интегрирования; x0 – значение начального условия; x – переменная (вектор библиотеки STL языка C++), куда будут добавляться узлы приближенного решения при выполнении численного интегрирования; h – шаг интегрирования; d – направление интегрирования (1 – прямое по времени, –1 – обратное по времени); info – вывод информации о вычислениях (да/нет); x_prev_t – указатель на вектор, содержащий сетку приближенных значений xN(t) на предыдущей итерации (с номером N) (по умолчанию равен NULL, так как, например, для решения уравнения Риккати он не нужен); u_prev_t – указатель на вектор, содержащий сетку приближенных значений векторной функции управления uN(t) на предыдущей итерации (с номером N) (по умолчанию равен NULL); K_t – указатель на вектор, содержащий уже полученную сетку приближенных значений (матриц) решения уравнения Риккати (по умолчанию равен NULL); H_t – указатель на вектор, содержащий сетку приближенных значений решения hN+1(t) уравнения (10) (по умолчанию равен NULL, нужен при решении уравнения (5), когда вычисляется управление по формуле (6)); u_t – указатель на вектор (по умолчанию тоже равен NULL, нужен при решении уравнения (5)), содержащий пересчитанную по формуле (6) сетку приближенных значений текущего управления uN+1(t) по сетке xN+1(t) и сетке, описывающей решение уравнения (10) в обратном времени. Представим фрагмент кода (полная программа приведена по ссылке [10]), в котором реализовано вычисление векторной функции f (см. правую часть уравнения (1)), а также решение векторного дифференциального уравнения (10): inline double f1() { return 0; } inline double f2(const double &phi, const double &omega) { return sys_alpha * omega * omega * sin(phi) * cos(phi) - sys_g * sin(phi); } inline double f3(const double &phi) { return sys_gamma * cos(phi); } inline vector_col calc_f_vect(const vector_col &x) { vector_col f_vect(3); f_vect(0) = f1(); f_vect(1) = f2(x(0), x(2)); f_vect(2) = f3(x(0)); return f_vect; } class eq_H: public rk4 { public: vector_col f(const double &t, const vector_col &x, const vector_col *x_prev, const vector_col *u_prev, const matrix *K, const vector_col *H) { return -prod(trans(a - prod(prod_brb, *K)), x) - prod(Q, calc_z_vect(t))+ prod(*K, calc_f_vect(*x_prev)); } }; Как видно, матричные операции в формуле (10) достаточно просто реализованы средствами языка C++, а точнее – использованы алгоритмы и шаблонные типы библиотеки uBLAS линейной алгебры собрания библиотек классов Boost. Было проведено профилирование кода решения задачи (1)–(3) с собственной реализацией матричных операций и с использованием uBLAS. Библиотека uBLAS дала большой выигрыш по времени решения данной задачи. Результаты решения задачи оптимального управления для системы (14) в графической форме приведены на сайте (см. http://www.swsys.ru/uploaded/image/2018-4/2018-4-dop/1.jpg). При этом за- даны следующие значения: T = 6, q1 = q2 = q3 = 3, kp = 10, b = 15, g = 1, b = 0,5, g = 9,8, kz = 1, dz = –1. Заключение Ключевым для настоящей работы является метод последовательных приближений (5)–(13). Для всех достаточно малых значений T метод (5)–(13) по построению равномерно сходится к решению задачи (1)–(3). При этом сходимость метода устанавливает существование решения задачи (1)–(3) для малых T и в пределе дает оптимальный закон управления с обратной связью. Исследование выполнено при финансовой поддержке РНФ в рамках научного проекта № 16-11-10352. Литература 1. Атанс М., Фалб П. Оптимальное управление. М.: Машиностроение, 1968. 764 с. 2. Беллман Р. Процессы регулирования с адаптацией. М.: Наука, 1964. 359 с. 3. Lukes D.L. Optimal regulation of nonlinear systems. SIAM J. Control Optim., 1969, vol. 7, pp. 75–100. 4. Yamamoto Y. Optimal control of nonlinear systems with quadratic performance. J. Math. Anal. Appl., 1978, vol. 64, pp. 348–353. 5. Dacka C. On the controllability of a class of nonlinear systems. IEEE Trans. Automat. Control, 1980, vol. 25, pp. 263–266. 6. Balachandran K., Somasundaram D. Existence of optimal control for nonlinear systems with quadraticperformance. J. Austral. Math. Soc, ser. B., 1987, vol. 29, pp. 249–255. 7. Afanas’ev A.P., Dzyuba S.M., Lobanov S.M., Tyutyun- nik A.V. Successive approximation and suboptimal control of systems with separated linear part. Appl. Comp. Math., 2003, vol. 2, no. 1, pp. 48–56. 8. Afanas’ev A.P., Dzyuba S.M., Lobanov S.M., Tyutyun- nik A.V. On a suboptimal control of nonlinearsystems via quadratic criteria. Appl. Comp. Math., 2004, vol. 3, no. 2, pp. 158–169. 9. Афанасьев А.П., Дзюба С.М. Об оптимальном управлении нелинейными системами по квадратичному критерию // Тр. ИСА РАН. 2008. Т. 32. С. 49–62. 10. Модуль stabil_task.cpp. 2018. URL: https://github.com/ alpchelintsev/stabil_task/blob/master/stabil_task.cpp (дата обращения: 13.07.2018). 11. Модуль rk4.hpp. 2018. URL: https://github.com/alpchelin tsev/stabil_task/blob/master/rk4.hpp (дата обращения: 13.07.2018). References
|
http://swsys.ru/index.php?page=article&id=4528&lang=&lang=%E2%8C%A9=en&like=1 |
|
Perhaps, you might be interested in the following articles of similar topics:
- Каркасная библиотека классов для объектно-ориентированного проектирования
- Реализация метаязыковой абстракции для поддержки ООП средствами языка Си
- Программная реализация метода автоматизированного проектирования фюзеляжа воздушного судна с помощью объектно-ориентированных технологий
- Оптимальное управление нелинейными системами по квадратичному критерию с ограничениями на управляющие воздействия
- Разработка прототипа информационно-технологического процесса обработки информации с учетом его стоимости


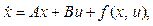 (1)
(1) i, j = 1, …, n;
i, j = 1, …, n; 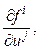 i = 1, …, n; j = 1, …, m в пространстве Rn+m.
i = 1, …, n; j = 1, …, m в пространстве Rn+m.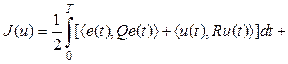
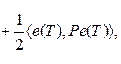 (3)
(3)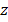 (t) устроен так, что указанное сведение невозможно.
(t) устроен так, что указанное сведение невозможно.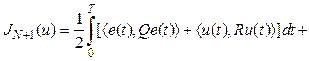
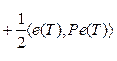 (4)
(4)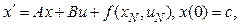 (5)
(5) (6)
(6)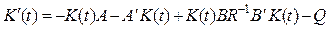 (8)
(8)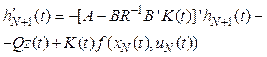 (10)
(10) (13)
(13) (14)
(14)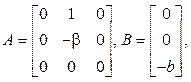
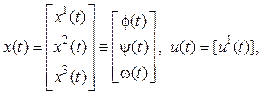
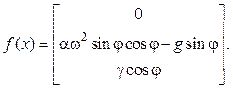
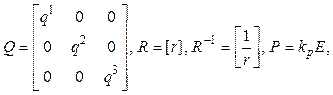
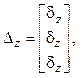 где kz – усиливающий коэффициент; dz – отклонение от рабочего режима z.
где kz – усиливающий коэффициент; dz – отклонение от рабочего режима z.