Математическое моделирование температурных полей в стеклоизделиях играет важнейшую роль при расчете процессов отжига стек- ла [1]. Геометрическая форма изделий может быть различной – плоской, цилиндрической. В таком случае одним из подходов при решении температурных задач является приведение сложного изделия к плоской форме за счет введения характерного или эффективного разме- ра [2]. Однако при этом точность расчетов ниже и не учитывается реальная геометрия тел цилиндрической формы. В данной работе рассматриваются подходы к моделированию тем- пературных полей в полых цилиндрических изделиях [3].
Для получения температурного поля необходимо решать дифференциальное уравнение теплопроводности в цилиндрических координатах:
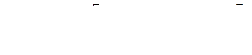 (1)
(1)
где t(r, t) – значение температуры в координате по радиусу r в момент времени t (°C); a – коэффициент температуропроводности материала изделия (м2/с) [4].
Большую роль для точного моделирования температурных распределений в изделиях играет корректный учет начальных и граничных условий, которые в большинстве стадий технологических процессов термообработки имеют сложный характер. Так, начальные условия обычно неравномерны, граничные условия соответствуют несимметричному конвективно-радиационному теплообмену поверхностей изделия с окружающей средой и ограждающими поверхностями (нагревательными элементами) технологического оборудования [5, 6]. В этом случае наиболее удобно применять численные конечно-разностные методы, при использовании которых частные производные в уравнении (1) по времени, координате 2-го и 1-го порядков заменяются на их численные аналоги: [ti+1(j) – ti(j)]/Dt, [ti(j – 1) – 2ti(j) + + ti(j + 1)]/(Dr)2 и [ti(j + 1) – ti(j)]/Dr. Здесь  – номер временной точки расчета;
– номер временной точки расчета; 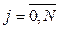 – номер точки по толщине; Dt – шаг по времени; Dr = (R2 – R1)/N – толщина слоя; R1, R2 – радиусы внутренней и внешней поверхностей полого цилиндра.
– номер точки по толщине; Dt – шаг по времени; Dr = (R2 – R1)/N – толщина слоя; R1, R2 – радиусы внутренней и внешней поверхностей полого цилиндра.
Тогда формулы для расчета температурного распределения во внутренних точках полого цилиндрического тела будут следующими:
 (2)
(2)
При расчете конвективного теплообмена необходимо приравнять тепловые потоки на поверхности, например, r = R1, в соответствии с законами Фурье – q(R1, t) = –l׶t(R1, t)/¶r и Ньютона – q(R1, t) = a1[(t(R1, t) – tc1(t)] [4]. Градиент ¶t(R1, t)/¶r = a1[(tc1(t) – t(R1, t)]/l, производные 2-го порядка 
 на внутренней r = R1 и внешней r = R2 поверхностях:
на внутренней r = R1 и внешней r = R2 поверхностях:
 (3)
(3)
где a1, a2 – коэффициенты конвективной теплоотдачи для внутренней и внешней поверхностей изделия (Вт/(м2град.)); tc1(t), tc2(t) – температура среды внутри и снаружи (°C); l – коэффициент теплопроводности материала (Вт/(м·град.)).
При расчете радиационного теплообмена с учетом закона Стефана–Больцмана по аналогии с (3) вторые производные на поверхностях r = R1 и r = R2 находятся по выражениям:
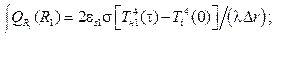 (4)
(4)
где es1, es2 – приведенные степени черноты верхней и нижней ограждающих поверхностей технологического оборудования; s = 5,67·10-12 (Вт/(м2K4)) – постоянная Стефана–Больцмана; Tн1(t), Tн2(t) – температуры ограждающих поверхностей над и под изделием (K).
C учетом передачи тепла точкам поверхностей изделия от внутренних соседних точек за счет теплопроводности получим окончательные выражения для расчета температур поверхностей цилиндрического тела в виде:
 (5)
(5)
Для проверки модели температурного поля (2)–(5) был произведен расчет конвективно-радиационного охлаждения полого бесконечного цилиндра при следующих значениях параметров: a = 0,2 (см2/мин.); l = 0,00838 (Вт/(см∙град.)); R1 = 0,3 (см); R2 = 0,6 (см); εs1 = εs2 = 0,91; N = 14; a1 = a2 = 0,001256 (Вт/см2∙град.); t0(j) = 707 (°C); tс1 = tс2 = 27 (°C); tн1= tн2 = 27 (°C); Dt = 0,03 (с). Результаты расчета температуры в цилиндрическом теле приведены в таблице 1.
Таблица 1
Распределение температуры в точках по толщине неограниченного полого цилиндра
Table 1
Temperature distribution at points along the thickness of an unlimited hollow cylinder
|
Температура
|
Время расчета t, с
|
|
0
|
6
|
10
|
20
|
30
|
60
|
120
|
¥
|
|
Внутренняя t(0)
|
707,0
|
619,6
|
584,2
|
511,8
|
456,4
|
344,8
|
226,8
|
27,0
|
|
Средняя t(N/2)
|
707,0
|
648,7
|
608,8
|
529,7
|
470,2
|
352,6
|
230,5
|
27,0
|
|
Внешняя t(N)
|
707,0
|
609,6
|
574,6
|
504,4
|
450,5
|
341,4
|
225,1
|
27,0
|
Решение поставленной задачи также мо- жет быть получено с помощью стандартной функции pdepe среды программирования Matlab [7, 8]. Характерные особенности разработки такой программы приведены в работе [9]. Функции типа дифференциального уравнения pdedif, начальных условий pdebeg и граничных условий pdebound не изменяются. Для учета цилиндрической формы тела необходимо задать константу формы m = 1.
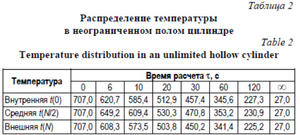
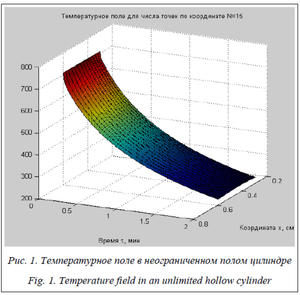 Результаты расчета температурного поля в неограниченном полом цилиндре с использованием стандартных функций Matlab приведены в таблице 2 и на рисунке 1. Разница с результатами, полученными с помощью конечно-разностных соотношений (2)–(5), не превышает 1 °C.
Результаты расчета температурного поля в неограниченном полом цилиндре с использованием стандартных функций Matlab приведены в таблице 2 и на рисунке 1. Разница с результатами, полученными с помощью конечно-разностных соотношений (2)–(5), не превышает 1 °C.
Для повышения точности мо- делирования процесса отжига необходимо учитывать конечные размеры стеклоизделий цилиндрической формы, в связи с чем возникает задача перехода от одномерного температурного поля по толщине изделия к двухмерному распределению, учитывающему градиенты температуры по высоте изделия. В пакете Matlab имеется набор инструментов для решения дифференциального уравнения теплопроводности в пространственных цилиндрических координатах, в частности, функция parabolic [7, 8]. Функция parabolic – решатель многомерных краевых задач методом конечных элементов [10] параболического дифференциального уравнения в частных производных:
 которое для случая осесимметричной температурной задачи в цилиндрической системе координат запишется следующим образом:
которое для случая осесимметричной температурной задачи в цилиндрической системе координат запишется следующим образом:
 (6)
(6)
где z – координата по высоте изделия; d = l/a, c = l – коэффициенты при производных; a1 = 0, f = 0 – отсутствующие множитель при температуре и внешний тепловой поток.
Для решения цилиндрической задачи с использованием parabolic необходимо произвести триангуляцию выбранной геометрической области с помощью функции initmesh. Обраще- ние к этой функции в Matlab выглядит следую- щим образом: [p, e, tr] = initmesh(g, 'Hmax', hmax), где g = decsg([3 4 – H/2 H/2 H/2 – H/2 R1 R1 R2 R2]') – описание геометрической области цилиндрического тела в прямоугольной системе координат; hmax – максимальный размер граничного элемента. Функция initmesh формирует выходные параметры: p – массив горизонтальных (по высоте) и вертикальных (по радиусу) координат узлов конечно-элементной сетки; e – матрица граничных элементов, содержащая номера начальных и конечных узлов этих элементов и номера граничных сегментов, которым они принадлежат; tr – матрица треугольных конечных элементов, содержащая номера входящих в них вершин (узлов).
 Визуальное изображение разбиения цилиндрической области на треугольные элементы, полученное с помощью функции pdeplot(p, e, t), показано на рисунке 2.
Визуальное изображение разбиения цилиндрической области на треугольные элементы, полученное с помощью функции pdeplot(p, e, t), показано на рисунке 2.
Обращение к решателю parabolic имеет синтаксис: uv = parabolic(u0, tauv, b, p, e, tr, c, a1, f, d), где uv – температурное поле в моменты времени tauv, для которых вычисляется решение уравнения (6); u0 – узловое распределение температуры в начальный момент времени t = 0; b = @boundaryFileHolParabolic – имя функции, вычисляющей матрицы описания граничных условий.
Граничные условия, при которых осуществляется решение задач параболического типа, могут быть 1-го (Дирихле) и 3-го (Неймана) рода и описываются уравнениями hu = r и 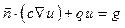 соответственно. Для рассматриваемой задачи конвективно-радиационного теплообмена граничные условия 1-го рода отсутствуют, поэтому коэффициенты h = r = 0.
соответственно. Для рассматриваемой задачи конвективно-радиационного теплообмена граничные условия 1-го рода отсутствуют, поэтому коэффициенты h = r = 0.
Граничные условия 3-го рода Неймана для температурной задачи:
–l׶t(r, t)/¶r + qt(r, t) = g. (7)
В то же время для конвективно-радиационного теплообмена на поверхностях цилиндрического тела (например, внутренней) по законам Ньютона и Стефана–Больцмана [3, 4]:
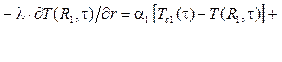 (8)
(8)
В связи с этим с учетом перехода к абсолютным температурам коэффициенты q, g в уравнении (7) для внутренней цилиндрической поверхности записываются в виде 

 Приведем текст функции граничных условий несимметричного конвективно-радиационного теплообмена конечного полого цилиндрического тела:
Приведем текст функции граничных условий несимметричного конвективно-радиационного теплообмена конечного полого цилиндрического тела:
function [ q, g, h, r ] = boundaryFileHolParabolic( p, e, u, time )
global alfa2 Tc2 es2 Tn2 sig umy alfa1 Tc1 es1 Tn1
N = 1; ne = size(e,2); q = zeros(N^2, ne); g = zeros(N, ne);
h = zeros(N^2, 2*ne); r = zeros(N, 2*ne);
xy1 = p(:,e(1,:)); xy2 = p(:,e(2,:));
xyMidEdge = (xy1+xy2)/2; y = xyMidEdge(2, i);
T1 = umy(e(1,:)); T2 = umy(e(2,:)); TMidEdge = (T1+T2)/2;
for i=1:ne
switch(e(5,i))
case 1
q(1,i) = (alfa1+es1*sig*TMidEdge^3)*y;
g(1,i) = (alfa1*Tc1+es1*sig*Tn1^4)*y;
case 3
q(1,i) = (alfa2+es2*sig*TMidEdge^3)*y;
g(1,i) = (alfa2*Tc2+es2*sig*Tn2^4)*y;
end
end
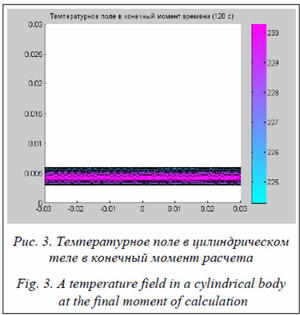 Результаты расчета двухмерного температурного поля в полом конечном цилиндрическом теле можно наглядно визуализировать с помощью функции Matlab pdeplot. Температурное поле в момент времени t = 2 мин. иллюстрирует рисунок 3.
Результаты расчета двухмерного температурного поля в полом конечном цилиндрическом теле можно наглядно визуализировать с помощью функции Matlab pdeplot. Температурное поле в момент времени t = 2 мин. иллюстрирует рисунок 3.
На рисунке видно отличное совпадение температурного распределения с результатами, полученными конечно-разностными методами и с помощью функции pdepe. Разработанные методы в перспективе позволяют перейти к решению задач моделирования температурного поля в сортовых стеклоизделиях цилиндрической формы (стакан, бутылка, колба), имеющих, кроме боковой, еще и донную поверхность. Предложенные модели температурного поля в дальнейшем можно использовать для идентификации условий теплообмена и оптимизации режимов термообработки стеклоизделий цилиндрической формы.
Литература
1. Гулоян Ю.А. Физико-химические основы технологии стекла. Владимир: Транзит-Икс, 2008. 736 с.
2. Мазурин О.В., Белоусов Ю.Л. Отжиг и закалка стекла. М.: Изд-во МИСИ и БТИСМ, 1984. 114 с.
3. Рубанов В.Г., Величко Д.В., Луценко О.В. Математическая модель динамики температурного поля стеклоизделий сложной конфигурации при их отжиге // Стекло и керамика. 2018. № 5. С. 3–8.
4. Формалеев В.Ф. Теплопроводность анизотропных тел. Ч. 1. Аналитические методы решения задач. М.: Физматлит, 2014. 349 с.
5. Мазурин О.В., Лалыкин Н.В. Математическая модель процесса отжига листового стекла // Стекло и керамика. 1984. № 1. С. 13–15.
6. Марголис Б.И. Программа идентификации условий теплообмена для изделий плоской формы // Программные продукты и системы. 2017. № 1. С. 148–151. DOI: 10.15827/0236-235X.117.148-151.
7. Дьяконов В.П. MATLAB: Полный самоучитель. М.: ДМК Пресс, 2014. 768 с.
8. Сирота А.А. Методы и алгоритмы анализа данных и их моделирование в MATLAB. СПб: БХВ-Петербург, 2016. 384 с.
9. Марголис Б.И. Программы моделирования температурных полей в изделиях плоской формы // Программные продукты и системы. 2016. № 2. С. 124–127. DOI: 10.15827/0236-235X.114.124-127.
10. Крайнов А.Ю., Миньков Л.Л. Численные методы решения задач тепло- и массопереноса. Томск: STT, 2016. 92 с.
References
- Guloyan Yu.A. Physical and Chemical Basics of Glass Technology. Vladimir, Tranzit-Iks, 2008, 736 p.
- Mazurin O.V., Belousov Yu.L. Annealing and Tempering Glass. Moscow, MISI i BTISM Publ., 1984, 114 p.
- Rubanov V.G., Velichko D.V., Lucenko O.V. A mathematical model of the temperature field dynamics of complex configuration glassware during annealing. Glass and Ceramics. Moscow, Ladya Publ., 2018, no. 5, pp. 3–8 (in Russ.).
- Formaleev V.F. Thermal Conductivity of Anisotropic Bodies. Part 1. Analytical Methods for Solving Problems. Moscow, Fizmatlit Publ., 2014, 349 p.
- Mazurin O.V., Lalykin N.V. A mathematical model of sheet glass annealing process. Glass and Ceramics. Moscow, Stroyizdat Publ., 1984, no. 1, pp. 13–15 (in Russ.).
- Margolis B.I. The program of identification of heat transfer conditions for flat products. Software & Systems. 2017, no. 1, pp. 148–151 (in Russ.). DOI: 10.15827/0236-235X.117.148-151.
- Dyakonov V.P. MATLAB: Full Self-Teaching Guide. Moscow, DMK Press, 2014, 768 p.
- Sirota A.A. Methods and Algorithms for Data Analysis and Modeling in MATLAB. St. Petersburg, BHV-Peterburg Publ., 2016, 384 p.
- Margolis B.I. Programs for modeling temperature fields in flat-shaped products. Software & Systems. 2016, no. 2, pp. 124–127 (in Russ.). DOI: 10.15827/0236-235X.114.124-127.
- Kraynov A.Yu., Minkov L.L. Numerical Methods for Solving Problems of Heat and Mass Transfer. Tomsk, STT Publ., 2016, 92 p.

 (2)
(2)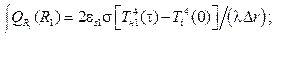 (4)
(4) (5)
(5)
 (6)
(6)

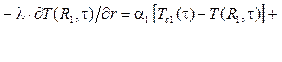 (8)
(8)