Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Оптимальное размещение модулей при проектировании распределенных тренажерных комплексов
Аннотация:
Abstract:
| Автор: Крестьянинов В.Б. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 8579 |
Версия для печати Выпуск в формате PDF (1.11Мб) |
Одной из основных и наиболее трудно решаемых задач разработки распределенных тренажерных систем на основе технологии DCOM (модель клиент-сервер) является задача оптимального распределения серверных компонентов (служб) по узлам локальной вычислительной сети (ЛВС). При фиксированном числе рабочих станций работу между ними можно распределить по-разному. В связи с этим встает задача определения такого распределения служб, при котором обеспечивается равномерная загрузка рабочих станций при ограниченной пропускной способности каналов связи. Пусть имеется n серверных служб, которые формируют определенный трафик для каждого рабочего места тренажерного комплекса, и m рабочих станций. Имеются данные о мощностях узлов сети и об объеме формируемого серверной службой трафика. Также известна загрузка j-го узла сети i-й серверной службой. Загрузка j-го узла сети основным процессом (рабочее место) одинакова и равна Т. Кроме того, на начальном этапе задается точность ∆. Необходимо так распределить серверные службы по узлам сети, чтобы минимизировать суммарную загрузку всего программного комплекса. Данные задачи представляются в виде таблицы, где
Поскольку на одном компьютере могут одновременно работать несколько процессов, то загрузка i-го узла представляется в виде уравнения:
где I – множество индексов, расположенных в i-м узле серверных служб. Необходимо учитывать ограничение на количество передаваемых по сети данных, поэтому определим:
где Bi – суммарный трафик расположенных в i-м узле серверных служб; B – максимально допустимый трафик. Тогда целевая функция примет вид:
Рассмотрим общую схему метода решения подобных задач. Пусть задача А состоит в нахождении такого элемента р* конечного множества Р, на котором достигается минимум функции F(X), определенной на этом множестве: Элементы множества Р, среди которых производится поиск, называются планами задачи А, а план р* – оптимальным планом задачи А. Метод построения последовательности планов [1,2] применим к задаче А, если выполняются следующие условия: 1) можно найти конечное расширение R множества Р(PÌR) и функцию Q(X) (миноранту), определенную на R, такую что Q(X); 2) можно построить алгоритм φ, который на k-м шаге находит элемент Если существует такое натуральное число k, при котором Схема работы метода ψ решения задачи A: 1) конструируется конечное расширение R исходного множества Р; 2) на множестве R задается функция Q(X), являющаяся минорантой функции F(X) на множестве Р; 3) формируется итеративный (но конечный) алгоритм φ, который на каждом шаге с номером k определяет оптимальный план 4) на каждом k-м шаге метода ψ проверяется выполнение критерия оптимальности. Если критерий выполняется, то процесс обрывается и Вспомогательную задачу минимизации миноранты Q(X) на множестве R будем называть задачей если если Пусть задача
заданной на множестве R векторов
где Таким образом, Непосредственно из определения h-оптимального плана следует, что Теперь можно сформулировать процедуру построения последовательности Алгоритм φ 1-й шаг: cреди множества k-й шаг (k=2,3,…): множество
Далее находим такой план, что Для решения функционального уравнения (4) необходимо знать значения функций Список литературы 1. Емиличев В.А., Комлик В.И. Метод построения последовательности планов для решения задач дискретной оптимизации. - М., 1981. 2. Корбут А.А., Финкельштейн Ю.Ю. Дискретное программирование - М., 1969. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=461 |
Версия для печати Выпуск в формате PDF (1.11Мб) |
| Статья опубликована в выпуске журнала № 3 за 2006 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Зарубежные базы данных по программным средствам вычислительной техники
- Исследовательское проектирование в кораблестроении на основе гибридных экспертных систем
- Реализация теней с помощью библиотеки OpenGL
- ДИНАМИКА-2 - программа для решения осесимметричных и плоских задач
- Место XML-технологий в среде современных информационных технологий
Назад, к списку статей



 – мощность i-го узла,
– мощность i-го узла,  ;
;  – сетевой трафик службы,
– сетевой трафик службы,  ;
; 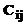 – загрузка j-го узла сети i-й серверной службой; ∆ – точность, причем
– загрузка j-го узла сети i-й серверной службой; ∆ – точность, причем  и
и 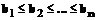 .
.

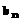

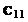






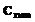
 , (1)
, (1) , (2)
, (2) , где
, где  ,
,  – мощность работы i-го узла.
– мощность работы i-го узла.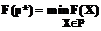 .
.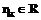 , обладающий свойством
, обладающий свойством  , где
, где 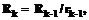
 , причем
, причем 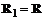 . При построениях по данному методу важное значение имеет следующий критерий оптимальности.
. При построениях по данному методу важное значение имеет следующий критерий оптимальности.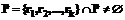 ,
, 
 , то
, то 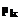 – оптимальный план задачи А.
– оптимальный план задачи А.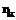 задачи минимизации функции Q(X) на множестве
задачи минимизации функции Q(X) на множестве  , образованном из расширения R путем исключения предыдущих оптимумов
, образованном из расширения R путем исключения предыдущих оптимумов 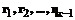 . Таким образом, алгоритм φ определяет последовательность оптимумов
. Таким образом, алгоритм φ определяет последовательность оптимумов 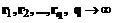 миноранты Q(X) на последовательности вложенных друг в друга множеств
миноранты Q(X) на последовательности вложенных друг в друга множеств  ;
;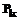 есть оптимальный план исходной задачи А. В противном случае переходим к (k+1)-му шагу метода ψ.
есть оптимальный план исходной задачи А. В противном случае переходим к (k+1)-му шагу метода ψ. . На предварительном этапе работы алгоритма строим функции
. На предварительном этапе работы алгоритма строим функции  , решая уравнения:
, решая уравнения: и
и  , то
, то  ;
; или
или 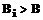 , то этот случай не рассматриваем.
, то этот случай не рассматриваем. состоит в минимизации сепарабельной функции
состоит в минимизации сепарабельной функции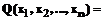
 , (3)
, (3)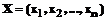 , удовлетворяющих условиям
, удовлетворяющих условиям  , где b>0,
, где b>0,  – целые числа. Здесь ω – операция сложения или умножения. Для этого следует воспользоваться следующим функциональным уравнением:
– целые числа. Здесь ω – операция сложения или умножения. Для этого следует воспользоваться следующим функциональным уравнением: , (4)
, (4) , причем
, причем  для
для  – оптимальное значение функционала задачи
– оптимальное значение функционала задачи  , в которой индекс n и параметр b заменены соответственно на k и z. Введем некоторые необходимые определения и обозначения. План
, в которой индекс n и параметр b заменены соответственно на k и z. Введем некоторые необходимые определения и обозначения. План 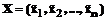 задачи
задачи 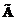 назовем h-оптимальным, если
назовем h-оптимальным, если 
 , и будем обозначать его
, и будем обозначать его 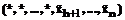 .
.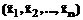 – оптимальный план задачи минимизации функции (3) при условиях
– оптимальный план задачи минимизации функции (3) при условиях  .
.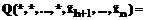
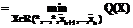 , где
, где 
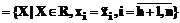 , то есть
, то есть  – множество всех тех планов задачи
– множество всех тех планов задачи  .
.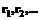 планов задачи
планов задачи  всевозможных (n-1)-оптимальных планов
всевозможных (n-1)-оптимальных планов  , … ,
, … ,  находим такой план
находим такой план 
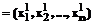 , что
, что  .
. преобразуем во множество
преобразуем во множество  по следующему правилу. Оставляем без изменения все планы множества
по следующему правилу. Оставляем без изменения все планы множества 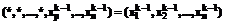 , который заменяем множеством
, который заменяем множеством  , состоящим из следующих планов:
, состоящим из следующих планов:

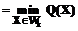 , и переходим к следующему шагу.
, и переходим к следующему шагу.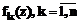 в промежуточных точках
в промежуточных точках  . Так как все типы данных задачи целочисленные (биты, секунды), то в качестве промежуточных точек будем брать лишь целые числа 1,…,b. Но и в этом случае при больших значениях b и при высокой точности (скажем, ∆=1) объем информации, которую необходимо вычислить, а главное, хранить, весьма велик. Все это делает актуальной проблему сокращения количества таких точек до числа, которое приемлемо при машинной реализации.
. Так как все типы данных задачи целочисленные (биты, секунды), то в качестве промежуточных точек будем брать лишь целые числа 1,…,b. Но и в этом случае при больших значениях b и при высокой точности (скажем, ∆=1) объем информации, которую необходимо вычислить, а главное, хранить, весьма велик. Все это делает актуальной проблему сокращения количества таких точек до числа, которое приемлемо при машинной реализации.