В настоящее время отмечается интерес к исследованию задач планирования совместных действий объектов сложных технических систем (СТС) или определения взаимодействия субъектов в социальных системах, объединенных общим функционалом, примерами которых являются задачи охраны протяженного периметра [1], обеспечения необходимых условий существования живых организмов в окружающей их среде [2], определения возможности распространения информации в социальных сетях с целью предотвращения угрозы терроризма [3, 4]. Все это обусловливает необходимость формализации как самого субъекта (объекта), выполняющего некоторые действия, так и отношений между ними и их взаимного влияния.
Исследования [5–8] привели к появлению и развитию акторно-сетевой теории (actor-network theory, ANT). ANT – подход в социальных исследованиях, который рассматривает сущности как действующие единицы социальных отношений (акторов). Совокупность акторов и взаимоотношения между ними создают плоскую динамическую сеть, определяющую их взаимодействие. Поскольку термин «актор» нашел применение не только в социологии, но и в других областях, включая компьютерные науки [9], будем полагать, что акторы – объекты или субъекты, обладающие общим функционалом в сети отношений с целью осуществления совместных действий (например, участие в информационном обмене).
Для системы охраны периметра в качестве акторов могут выступать стационарные или подвижные объекты охраны (ОО), необитаемые интеллектуальные взаимодействующие мобильные роботизированные платформы (НИВМРП), предназначенные для сбора данных об ОО, потенциальные нарушители охраняемого периметра, компьютер (как ЛПР), обрабатывающий информацию о состоянии ОО и возможных проникновениях на территорию. Совместное взаимодействие акторов обеспечивает функцию охраны протяженного объекта. Здесь в качестве отношений между акторами можно рассматривать близость ОО или НИВРМП и ОО, потоки данных и управляющих сигналов.
Для исследования взаимодействия акторов существуют несколько различных методов, в том числе нейросетевое, когнитивное моделирование, вычисления на графах.
Примеры использования нейросетевых технологий для исследования взаимодействия субъектов и объектов рассмотрены в [10, 11]. К недостаткам нейросетевых подходов следует отнести потребность в большом количестве ретроспективной информации для качественного обучения сети и сложность ее анализа, вследствие чего обученная нейронная сеть является для пользователя черным ящиком. К тому же нейросетевые подходы не позволяют представить сложный объект одной вершиной, что значительно усложняет исследования.
Для моделирования взаимодействия сложных технических объектов (устройств) применяются когнитивные и нечеткие когнитивные подходы [12–15]. При использовании когнитивных подходов к моделированию взаимодействия акторов возможны случаи потери информации, так как такие модели не учитывают существующие разнотипные отношения между акторами и для каждого типа отношений необходимо формировать отдельную модель.
Для моделирования сложного взаимодействия акторов и планирования их совместной деятельности предлагается использовать подход на основе графов. Графовые модели позволяют представить акторы, например, в виде вершин, отразить сеть их отношений посредством связей между вершинами, а также выполнить вычисления в модели с целью планирования поведения акторов. Для нечетких графов весовые коэффициенты ребер и вершин могут соответствовать степени принадлежности нечеткому множеству. Наряду с этим в работе [16] обосновывается необходимость использования однотипных и разнотипных связей для представления существующих отношений между акторами в графовых моделях. С целью снижения временных затрат на организацию вычислений в таких моделях предлагается использовать совокупность однотипных, разнотипных связей и связей в виде векторов (далее – множественные связи в графе или множественные отношения в модели) [17].
В рамках данной статьи граф с однотипными связями будем называть моделью 1, граф с однотипными и разнотипными связями – моделью 2, а граф с учетом множественных связей – моделью 3. Представление графа возможно в виде матриц или списков [18]. В работах [19, 20] отмечается целесообразность использования списков для представления гра- фовых моделей 2 и 3, что связано с избыточно- стью их матричного представления и сложностью представления в виде двумерной матрицы из-за большого числа атрибутов ребер.
В статье предлагается и исследуется нечеткая модель взаимодействия акторов (НМВА) на основе графа с учетом множественных связей и описывается ее программная реализация.
НМВА на основе графа с учетом множественных связей
Введем формальное описание нечеткой модели графа с учетом множественных связей: Gʹ = (Gʹv, Gʹe), где Gʹv = {gvi}, Gʹe = {gej} – конечные множества вершин с атрибутами gvi (graph vertex) и ребер с атрибутами gej (graph edge) соответственно. В качестве атрибутов вершин могут выступать их весовые коэффициенты, а атрибутов ребер – веса, ориентация, вид связи. Ребра могут быть ориентированными (связи gvi ® gvj) или неориентированными (связи gvi – gvj), а связи – однотипными (gvi – gvj и gvi ® gvj), разнотипными (связи gvi – tp – gvj и gvi – tp ® gvj, где tp – type) и множественными в виде вектора (связи gvi – v̅ ® ® gvj и gvi – v̅ – gvj). Ребро в виде вектора представляется как v̅ = , где t – размерность вектора (кратность ребра v̅ ).
Весу связи в графе может придаваться смысл меры достоверности (меры правдоподобия) или степени принадлежности нечеткому множеству. Степени принадлежности присутствуют в матрицах либо в списках, задающих граф. Они могут определяться экспертом, ЛПР либо вычисляться посредством фаззифика- ции [21]. В графе Gʹ значению веса ребра μi Î [0, 1] может придаваться смысл степени удаленности акторов или меры достоверности передачи информации между акторами, а весу вершины hi Î [0, 1] – меры значимости акторов или степени их удаленности.
Рассмотрим возможности использования, а также преимущества и недостатки известных ранее моделей 1, 2 и предложенной в статье модели 3 для моделирования СТС на примере системы охраны протяженного периметра, которая состоит из десяти ОО (ОО1–ОО10), двух НИВРМП (ТУ1, ТУ2) и одного ЛПР, обрабатывающего потоки данных от НИВРМП и формирующего управляющие сигналы для их перемещения. При этом в моделях необходимо учесть параметр близости ОО и возможности НИВРМП по наблюдению за ними. Для реше- ния этой задачи воспользуемся разработанным автором программным модулем для представ- ления акторов и их отношений на основе графов [22], который позволяет реализовать модели 1–3.
Описание программного модуля для представления акторов и их отношений на основе графов
 Данный программный модуль предназначен для представления акторов и отношений между акторами в графовой модели и является частью программного комплекса моделирования взаимодействия акторов и их групп, реализованного на языке C++ с использованием библиотеки Qt [23]. Все используемые средства реализации являются кроссплатформенными, что обусловливает возможность функционирования программного модуля в различных операционных системах. Структура программного модуля представлена на рисунке 1 и состоит из ряда блоков.
Данный программный модуль предназначен для представления акторов и отношений между акторами в графовой модели и является частью программного комплекса моделирования взаимодействия акторов и их групп, реализованного на языке C++ с использованием библиотеки Qt [23]. Все используемые средства реализации являются кроссплатформенными, что обусловливает возможность функционирования программного модуля в различных операционных системах. Структура программного модуля представлена на рисунке 1 и состоит из ряда блоков.
Блок редактирования графа представляет собой визуальный редактор, в котором пользователь может создавать графы. Первоначально граф задается в виде графического изображения. Редактор позволяет производить различные операции над элементами структуры графа: перемещать, удалять и выделять вершины, соединять две вершины друг с другом и т.д. Вершины в графе принадлежат к одному типу, а связи могут быть однотипными, разнотипными и множественными в виде вектора. Граф может быть ориентированным, неориентированным или смешанным, с одной стороны, и взвешенным или невзвешенным, с другой. Взвешенный граф может иметь связи и вершины с весовыми коэффициентами. В качестве вершин графа могут выступать акторы, а отношения между ними могут быть заданы связями в графе.
Сразу после загрузки (посредством блока загрузки графа) или по мере создания графа (блок редактирования графа) определяются его основные параметры. Полученный граф сохраняется в блоке хранения графа и посредством блока отображения выводится на экран. Структура графа заносится в .xml-файл, в котором хранятся описание его вершин, ребер и списковое представление его текущего состояния.
Разработка НМВА для моделирования СТС
Модель 1. Для моделирования заданной системы охраны разработан смешанный нечеткий граф Gʹ1 с учетом однотипных связей, заданный множествами вершин G1ʹv = {gv1, gv2, …, gv12} и ребер G1ʹe = {ge1, ge2, …, ge25}. При этом вершины в графе соответствуют акторам НМВА, а ребра – отношениям между акторами. Акторы a1, a2 (вершины gv1, gv2) представляют ТУ1, ТУ2, а акторы a3–a12 (вершины gv1–gv12) – охраняемые объекты ОО1–ОО10.
Вершины в графе G1ʹ имеют веса: для вершин gv1, gv2 – значение 0,5; для вершин gv3–gv12 – значение 0,2. В модели сочетаются однотипные связи двух видов, при этом ориентированному ребру (gvi ® gvj) придается смысл связи ТУ и ОО, неориентированному ребру (gvi – gvj) – связи между ОО. Веса ребер соответствуют степени близости акторов.
Следует отметить, что ограничение на однотипность связей в модели не позволяет использовать ЛПР для приема и выдачи разнотипных (информационных и управляющих) сигналов. Эта проблема может быть решена в модели 2.
Модель 2. Эта модель позволяет сочетать однотипные и разнотипные ребра, что дает возможность представить ЛПР, а также совокупность необходимых информационных и управляющих сигналов. Нечеткий граф Gʹ2, моделирующий систему охраны с учетом однотипных и разнотипных связей, задается множествами вершин G2ʹv = {gv1, gv2, …, gv13} и ребер G2ʹe = {ge1, ge2, …, ge33}. Отличия графа G2ʹ от графа в модели 1 следующие: актор a13 (вершина gv13) представляет ЛПР и разнотипные ребра ge29, ge33 (gvi – tp ® gvj), и однотипные ge26–ge28, ge30–ge32 (gvi – tp – gvj). Неориентированные разнотипные ребра демонстрируют возможность передачи информации по различным каналам: tp1 – Wi-Fi, tp2 – Bluetooth, tp3 – низкочастотный радиоканал, а их веса соответствуют вероятностям использования канала. Разнотипные ориентированные ребра задают действия акторов, например, tp4 – «управлять движением», их веса соответствуют заданному направлению движения.
Таким образом, использование однотипных и разнотипных связей в графе G2ʹ позволило задать все необходимые отношения между акторами в модели 2. Далее рассмотрим возможности использования модели 3 для представления заданных отношений на примере графа G3ʹ.
Модель 3. Данная модель допускает использование множественных связей, поэтому с целью снижения числа ребер в графе предлагается объединение ряда разнотипных связей в одну связь вида gvi – v̅ – gvj, в нашем случае это связи tp1, tp2, tp3.
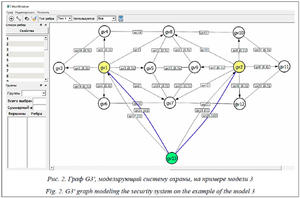 Тогда граф G3ʹ (рис. 2), заданный множествами вершин G3ʹv = {gv1, gv2, …, gv13} и ребер G3ʹe = {ge1, ge2, …, ge29}, содержит на 4 ребра меньше, чем граф в модели 2. Вершины в графе соответствуют акторам НМВА, а ребра – отношениям между акторами. Акторы a1, a2 (вершины gv1, gv2) представляют ТУ1, ТУ2, акторы a3–a12 (вершины gv1–gv12) – ОО1–ОО10, актор a13 (вершина gv13) – ЛПР (табл. 1). Веса вершин hi соответствуют следующим значениям: h1, h2 – 0,5, h3 – h12 – 0,2, h13 – 1,0, которые интерпретируются как степень значимости актора, то есть фактически зависят от назначе- ния актора, что может быть полезным при дальнейшей обработке НМВА. Граф G3ʹ содержит ребра (табл. 2), при этом ориентированным ребрам ge1–ge12 придается смысл связи ТУ и ОО (отношение «наблюдать»), неориентированным ребрам ge12–ge25 – связи между ОО (отношение «связь ОО»). В модели (рис. 2) веса ребер ge указаны в скобках (численное значение 0,5), при этом, если вес ребра не указан, значит, он соответствует значению 1,0. Вес ребра соответствует степени близости акторов.
Тогда граф G3ʹ (рис. 2), заданный множествами вершин G3ʹv = {gv1, gv2, …, gv13} и ребер G3ʹe = {ge1, ge2, …, ge29}, содержит на 4 ребра меньше, чем граф в модели 2. Вершины в графе соответствуют акторам НМВА, а ребра – отношениям между акторами. Акторы a1, a2 (вершины gv1, gv2) представляют ТУ1, ТУ2, акторы a3–a12 (вершины gv1–gv12) – ОО1–ОО10, актор a13 (вершина gv13) – ЛПР (табл. 1). Веса вершин hi соответствуют следующим значениям: h1, h2 – 0,5, h3 – h12 – 0,2, h13 – 1,0, которые интерпретируются как степень значимости актора, то есть фактически зависят от назначе- ния актора, что может быть полезным при дальнейшей обработке НМВА. Граф G3ʹ содержит ребра (табл. 2), при этом ориентированным ребрам ge1–ge12 придается смысл связи ТУ и ОО (отношение «наблюдать»), неориентированным ребрам ge12–ge25 – связи между ОО (отношение «связь ОО»). В модели (рис. 2) веса ребер ge указаны в скобках (численное значение 0,5), при этом, если вес ребра не указан, значит, он соответствует значению 1,0. Вес ребра соответствует степени близости акторов.
Для оценки значения показателей весов ребер графа G3ʹ и рассмотренных ранее G2ʹ и G1ʹ введено вербальное описание (очень слабый показатель, слабый показатель, умеренный показатель, сильный показатель, очень сильный показатель) с соответствующими определениями значений весов посредством числовых интервалов или нечетких множеств.
Неориентированные ребра в виде вектора ge26, ge28 (связи gvi–v̅–gvj) демонстрируют возможность передачи информации по различным каналам: v1 – Wi-Fi, v2 – Bluetooth, v3 – низкочастотный радиоканал (УКВ), а их веса μj соответствуют вероятностям использования канала: так, μ26 = (0,1; 0,3; 0,8) означает, что для передачи информации будет использоваться УКВ со значением вероятности 0,8, а μ28 = (0,2; 0,9; 0,3) – канал Bluetooth. Ориентированные разнотипные ребра ge27, ge29 задают действия акторов, например, позволяют передавать управляющие сигналы от ЛПР к ТУ (отношение tp1 – управлять движением), их веса μj соответствуют заданному направлению движения (например, по часовой стрелке или против).
Таблица 1
Соответствие акторов и вершин в графе G3ʹ
Table 1
The correspondence between actors and vertexes in G3ʹ graph
|
Назначение актора
|
Актор
|
Вершина графа
|
Вес вершины, hi
|
|
НИВРМП
(ТУ1 и ТУ2)
|
a1, a2
|
gv1, gv2
|
По 0,5
|
|
Объекты охраны
(ОО1–ОО10)
|
a3–a12
|
gv3–gv12
|
По 0,3
|
|
Компьютер (ЛПР)
|
a13
|
gv13
|
1,0
|
Таблица 2
Соответствие отношений акторов ребрам графа G3ʹ
Table 2
The correspondence of the actor relations to the edges of G3ʹ graph
|
Вид ребра
|
Вид связи
|
Отношение между акторами
|
Ребро графа, ge
|
|
Однотипное
|
gvi ® gvj
|
Наблюдать
|
ge1–ge12
|
|
gvi–gvj
|
Связь ОО
|
ge12–ge25
|
|
Вектор
|
gvi – v̅ – gvj
|
Передача информации по каналам:
v1 – Wi-Fi,
v2 – Bluetooth,
v3 – УКВ
|
ge26, ge28
|
|
Разнотипное
|
gvi – tp ® gvj
|
tp1 – управлять движением
|
ge27, ge29
|
Следует отметить, что модель 3 за счет использования множественных связей позволяет снизить число разнотипных ребер в графе по сравнению с моделью 2.
Заключение
В работе представлены результаты разработки трех НМВА для моделирования сложных технических систем на примере решения задачи обеспечения охраны протяженного периметра. Для моделирования использован программный модуль представления акторов и их отношений в графовых моделях. Модель 1, учитывающая только однотипные связи, не может использоваться для решения данной задачи, так как не позволяет в полной мере представить необходимые объекты системы охраны и их отношения. Модель 2 с учетом однотипных и разнотипных связей дает возможность представить все необходимые объекты системы охраны и отношения между ними и, следовательно, позволяет решить задачу моделирования системы охраны. Предложенная в статье модель 3, сочетающая однотипные, разнотипные связи и связи в виде вектора, позволяет снизить число ребер в графе и уменьшить временные затраты на организацию вычислений в НМВА по сравнению с моделью 2 при условии сохранения требуемого количества акторов и отношений между ними. Результаты экспериментальных исследований применения программного модуля для графов от 300 до 1 000 вершин показали уменьшение временных затрат на формирование матрицы расстояний в модели 3 по сравнению с моделью 2 от 1,5 до 3,9 раза, что подтверждает эффективность и предпочтительность модели 3 для практического использования.
Работа выполнена в рамках проектной части госзадания Минобрнауки России № 2.3928.2017/4.6 в Южном федеральном университете.
Литература
1. Полянский И.С., Беседин И.И., Панин Б.Л. Математическая модель комплекса инженерно-технических средств системы физической защиты объекта охраны // Фундаментальные исследования: Технич. науки. 2013. № 6. С. 1359–1365.
2. Шмелева И.А. Проблема взаимодействия человека с окружающей средой: области и аспекты психологического исследования // Вестн. МГУ. 2010. № 3. С. 105–120.
3. Носова М.В., Сенникова Л.И. Моделирование распространения информации в децентрализованных сетевых системах с нерегулярной структурой // Новые информационные технологии в автоматизированных системах. 2014. № 17. С. 329–335.
4. Liben-Nowell D., Kleinberg J. Tracing information flow on a global scale using Internet chain-letter data. PNAS, 2008, vol. 105, pp. 4633–4638.
5. Latour B. Politics of nature. How to bring the sciences into democracy. HUP Publ., UK, 2004, 320 p.
6. Латур Б. Пересборка социального. Введение в акторно-сетевую теорию. М.: ГУ-ВШЭ, 2014. 384 с.
7. Ло Дж. Объекты и пространства // Социологическое обозрение. 2006. № 1. С. 30–42.
8. Mol A. The Body Multiple: Ontology in Medical Practice. Duke Univ. Press, 2002, vol. 2, pp. 281–282. DOI: https://doi.org/10.1017/S174585520722558X.
9. Srinivasan S., Mycroft A. Kilim isolation-typed actors for Java. Proc. ECOOP, 2008, pp. 104–128.
10. Мисюра В.В., Кондратьева Т.Н., Бенгус Б.В. Сравнительный анализ методов прогнозирования тенденции развития временных рядов // Вестн. РГУПС. 2014. № 2. С. 124–128.
11. Круглов В.В., Дли М.И. Применение аппарата нейронных сетей для анализа социологических данных // Социологические исследования. 2001. № 9. С. 112–114.
12. Башлыков А.А., Еремеев А.П. Основы конструирования интеллектуальных систем поддержки принятия решений в атомной энергетике. М.: ИНФРА-М, 2018. 351 с.
13. Горелова Г.В., Мельник Э.В., Коровин Я.С. Когнитивный анализ, синтез, прогнозирование развития больших систем в интеллектуальных РИУС // Штучний інтелект. 2010. № 3. C. 61–72 (рус.).
14. Kolodenkova A.E., Muntyan E.R., Korobkin V.V. Modern approaches to modeling of risk situations during creation complex technical systems. AISC. 2018, vol. 875, pp. 209–217.
15. Кузнецов О.П. Когнитивное моделирование слабо структурированных ситуаций // Искусственный интеллект – проблемы и перспективы: матер. конф. М., 2006. С. 86–100.
16. Сергеев Н.Е., Целых А.А. Нечеткие теоретико-графовые подходы к моделированию и анализу социосемантических сетей знаний для задач принятия решений в научной и научно-технической экспертизе // Науч. журн. КубГАУ. 2016. № 09. С. 1–21. URL: http://ej.kubagro.ru/2016/09/pdf/27.pdf (дата обращения: 15.05.2019).
17. Сергеев Н.Е., Мунтян Е.Р. Использование списков для представления социальных отношений // Информатизация и связь. 2018. № 4. С. 43–49.
18. Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы. Построение и анализ. М.: Вильямс, 2013. 1328 с.
19. Сергеев Н.Е., Мунтян Е.Р., Целых А.А., Самойлов А.Н. Обобщение графов ситуаций на основе спискового алгоритма свертки для задач ситуационного управления // Изв. ЮФУ: Технич. науки. 2017. № 3. С. 111–121.
20. Сергеев Н.Е., Мунтян Е.Р. О решении некоторых задач, возникающих при моделировании взаимодействия социальных групп // Системный синтез и прикладная синергетика: сб. тр. VIII Всерос. науч. конф. Таганрог: Изд-во ЮФУ, 2017. С. 240–249.
21. Аверкин А.Н., Батыршин И.З. и др. Нечеткие множества в моделях управления и искусственного интеллекта. М.: Наука, 1986. 312 с.
22. Мунтян Е.Р. Программный модуль для представления акторов и отношений между акторами на основе графов. Свид. о гос. регистр. прогр. для ЭВМ № 2018665499; зарегистр. 05.12.2018. М.: Роспатент, 2018.
23. Мунтян Е.Р. Разработка программного комплекса для моделирования взаимодействия акторов и их групп на основе графов // Инновационные технологии и дидактика в обучении: сб. стат. Междунар. науч.-практич. конф. Таганрог: Изд-во ЮФУ, 2018. Т. 1. С. 74–78.
References
- Polyansky I.S., Besedin I.I., Panin B.L. A mathematical model of the complex of engineering and technical means of the system of protection object physical protection. Fundamental Research. Engineering Sciences. 2013, no. 6, pp. 1359–1365 (in Russ.).
- Shmeleva I.A. The problem of human-environment interactions: areas and aspects of psychological study. Bulletin of Moscow Univ. Psychology. 2010, no. 3, pp. 105–120 (in Russ.).
- Nosova M.V., Sennikova L.I. Modeling of information distribution in decentralized network systems with an irregular structure. New information Technologies in Automated Systems. 2014, no. 17, pp. 329–335 (in Russ.).
- Liben-Nowell D. and Kleinberg J. Tracing information flow on a global scale using Internet chain-letter data. PNAS. 2008, no. 105, pp. 4633–4638.
- Latour B. Politics of Nature. How to Bring the Sciences into Democracy. Cambridge, Harvard Univ. Press, 2004, 320 p.
- Latour B. Social Reassembly. Introduction to the Actor-Network Theory. Moscow, HSE Publ., 2014, 384 p.
- Lo J. Objects and spaces. Sociological Studies. 2006, no. 1, pp. 30–42 (in Russ.).
- Mol A. The Body Multiple: Ontology in Medical Practice. Durham, Duke Univ. Press, 2002. DOI: https://doi.org/10.1017/S174585520722558X.
- Srinivasan S., Mycroft A. Kilim: Isolation-typed actors for Java. Proc. ECOOP. 2008, pp. 104–128.
- Misyura V.V., Kondratieva T.N., Bengus B.V. Comparative analysis of methods of forecasting the trend of time series development. Bulletin of Rostov State Transport Univ. 2014, no. 2, pp. 124–128 (in Russ.).
- Kruglov V.V., Dli M.I. Application of neural network apparatus for analysis of sociological data. Sociological Studies. 2001, no. 9, pp. 112–114 (in Russ.).
- Bashlykov A.A., Eremeev A.P. Fundamentals of Design of Intelligent Decision Support Systems in Nuclear Power Engineering. Moscow, INFRA-M Publ., 2018, 351 p.
- Gorelova G.V., Melnik E.V., Korovin Yu.S. Cognitive analysis, synthesis, forecasting of the development of large systems in intellectual RIUS. Artificial Intelligence. 2010, pp. 61–72 (in Russ.).
- Kolodenkova A.E., Muntyan E.R., Korobkin V.V. Modern approaches to modeling of risk situations during creation complex technical systems. AISC. 2018, vol. 875, pp. 209–217.
- Kuznetsov O.P. Cognitive modeling of semi-structured situations. Proc. Conf. Pospelov Readings “Artificial intelligence – problems and prospects”. Moscow, 2006, pp. 86–100 (in Russ.).
- Sergeev N.E., Tselykh A.A. Fuzzy graph theoretic approaches to modeling and analysis of sociosemantic knowledge networks for the tasks of decision making in scientific and technical expertise. Scientific J. of KubSAU. Krasnodar, KubSAU, 2016, no. 09, pp. 1–21. Available at: http://ej.kubagro.ru/2016/09/pdf/27.pdf (accessed May 15, 2019).
- Sergeev N.E., Muntyan E.R. Usage of lists to represent social relations. Informatization and Communication. 2018, no. 4, pp. 43–49 (in Russ.).
- Cormen T., Leiserson C., Rivest R., Stein K. Algorithms: Construction and Analysis. 3rd ed., Moscow, Vilyams Publ., 2013, 1328 p.
- Sergeev N.E., Muntyan E.R., Tselykh A.A., Samoylov A.N. Situation graph generalization for situation awareness using a list-based folding algorithm. Izvestiya SFedU. Engineering sciences. 2017, no. 3,
pp. 111–121 (in Russ.).
- Sergeev N.E., Muntyan E.R. About solution of some problems, arising in the modeling of the interaction of social groups. Proc. of 8th All-Russ. Sci. Conf. on System Synthesis and Applied Synergetics. Rostov-on-Don, Taganrog, SFU Publ., 2017, pp. 240–249 (in Russ.).
- Averkin A.N., Batyirshin I.Z. Fuzzy Sets in Management Models and artificial Intelligence. D.A. Pospelov (Ed.). Moscow, Science Publ., 1986.
- Muntyan E.R. A Software Module for Representing Actors and Relations Between Actors Based on Graphs. Certificate of registration of a computer program no. 2018665499. Moscow, Rospatent, 2018.
- Muntyan E.R. Development of software to simulate the interaction of actors and their groups based on graphs. Proc. Intern. Sci. and Pract. Conf. on Innovative Technologies and Didactics in Teaching. Taganrog, SFU Publ., 2018, vol. 1, pp. 74–78 (in Russ.).





