Морским поисково-спасательным операциям уделяется огромное внимание. Практически все морские державы имеют утвержденные на государственном уровне планы мероприятий по поиску и спасанию (search and rescue –SAR) [1, 2]. Исходя из важности и стоимости таких мероприятий, большое значение придается их эффективности. Так, в американском национальном плане SAR отмечается важность эффективного использования всех доступных ресурсов во всех типах гражданских поисково-спасательных операций и сотрудничества в предоставлении оперативных и эффективных услуг. Кроме того, отмечается стремление применять наиболее эффективные системы для спасания большинства жизней при минимальных операционном риске и стоимости [2].
Методы повышения эффективности SAR постоянно разрабатываются и совершенствуются. Так, для моделирования надежности операций поиска и спасания в координационных центрах береговой охраны Великобритании предлагается применять методологию байесовских сетей наряду с используемой методологией бинарной логистической регрессии для поддержки анализа, каждая из которых имеет как свои преимущества, так и недостатки [3]. Основная цель разработанной для канадских вооруженных сил географической системы поддержки принятия решений SARPlan заключается в оптимизации планирования поисковых миссий для пропавших самолетов. Ее модули оптимизации основаны на теории поиска и методах градиентного поиска и направлены на максимизацию вероятности успеха миссии при обеспечении доступности поисковых ресурсов. Наряду с увеличением шансов найти потерянный самолет и выживших людей ее применение должно приводить к снижению эксплуатационных расходов [4].
Роль использования эмпирических зависимостей во многих областях человеческой деятельности сложно переоценить. Строгие математические модели описывают только отдельные аспекты реальных процессов или их идеализированные представления. Обычно это заключается во внесении в идеализированные математические модели различных поправочных коэффициентов или выражений, определяемых в зависимости от различных отклонений реальных условий от идеализированных.
Подобный подход применяется и в методике оценки эффективности поисково-спасательного обеспечения (ПСО) в операциях (боевых действиях) объединений и группировок сил (войск) ВМФ [1]. Она разработана в соответствии с Концепцией развития системы поисково-спасательного обеспечения ВМФ на период до 2025 года. Ее основные положения реализованы в комплексе средств автоматизации морской спасательной операции. В методике под эффективностью системы ПСО сил флота понимается доля аварийных объектов из общего количества аварийных объектов, находящихся в районе, которым в результате поисково-спасательных действий (ПСД) силами ПСО флота будет оказана помощь. Методика позволяет прогнозировать эффективность различных возможных (наиболее вероятных) ва- риантов ПСД для выбора наиболее эффективного варианта.
Существующая методика
Эффективность ПСД в каждом из случаев различного количества одновременно находящихся в районе ПСД аварийных объектов определяется как вероятность оказания помощи заданному количеству аварийных объектов, а результирующая эффективность системы ПСО при выбранном варианте вычисляется по совокупности всех возможных случаев с учетом их вероятности. Расчет эффективности ПСД в каждом конкретном случае базируется на вероятности оказания помощи аварийным объектам без учета внешних воздействий и корректируется вероятностью PВВ неблагоприятного внешнего воздействия на ход ПСД. Практическая применимость методики для выбора наиболее эффективных ПСД в значительной мере определяется адекватностью оценки этой величины.
Неблагоприятные внешние воздействия на ход ПСД рассматриваются в методике как попарно независимые и совместные вероятностные события таких внешних факторов, как гидрометеорологические и физико-географические условия, противодействие противника (далее в данной работе не рассматривается) и неблагоприятные технические факторы. К последним относятся несоответствие характера аварии тактико-техническим возможностям спасательного отряда, техническое состояние спасательных судов и средств спасания, степень их надежности. Таким образом, в мирное время вероятность PВВ неблагоприятного внешнего воздействия на ход ПСД определяется как
PВВ = PГМУ + PТ – PГМУ ´ PТ, (1)
где PГМУ – вероятность неблагоприятного воздействия гидрометеорологических и физико-географических условий; PТ – вероятность воздействия неблагоприятных технических факторов. Вероятность этих неблагоприятных внешних воздействий зависит от присущих им неблагоприятных факторов, снижающих эффективность ПСО, которые также принимаются попарно независимыми. Для более объективного учета в методике неблагоприятным факторам присваиваются определенные веса в зависимости от ожидаемой степени их воздействия на конечный результат поиска аварийных объектов, перехода в район аварийных объектов и выполнения задач ПСО в районе аварийных объектов, рассматриваемых как виды деятельности сил и средств ПСО. Именно эти веса выполняют роль своего рода поправочных коэффициентов учета различных отклонений реальных условий от идеализированных, описанных математической моделью (см. таблицу).
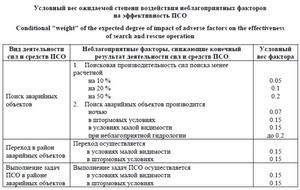
В качестве примера предположим, что поисковая производительность сил поиска менее расчетной на 10 % (условный вес 0.05), поиск аварийных объектов производится при малой видимости (условный вес 0.15), а остальные неблагоприятные факторы отсутствуют. Тогда, по существующей методике, вероятность неблагоприятного внешнего воздействия на ход ПСД составит: PВВ = 0.05 + 0.15 – 0.05 ´ 0.15 = = 0.19.
В данном случае оба неблагоприятных фактора воздействуют только при поиске аварийных объектов, что позволяет воспользоваться формулой (1) непосредственно. Однако добавление в данный пример условий малой видимости (условный вес 0.15) также при переходе в район аварийных объектов и при выполнении задач ПСО в районе аварийных объектов в соответствии с методикой оставляет величину PГМУ, а следовательно, и величину PВВ неизменными, что требует корректировки. В таблице условиям малой видимости при различных видах деятельности сил и средств ПСО могут быть присвоены различные условные веса, однако методика не дает прямого ответа на вопрос, какое значение в этом случае использовать в качестве PГМУ. Кроме того, к существенному огрублению результата приводит отсутствие градаций неблагоприятных факторов, снижающих эффективность ПСО (кроме поисковой производительности сил поиска менее расчетной), что во многом обусловливается их нерасчетным характером. Решить эти проблемы только предлагаемым в методике средством – возможной корректировкой, расширением и дополнением содержания таблицы с условными весами на основе результатов проведения специальных учений сил ПСО флота – невозможно.
Сущность предлагаемого нечеткого подхода
Для преодоления указанных проблем предлагается, во-первых, предположить попарную независимость и совместность вероятностных событий различных видов деятельности сил и средств ПСО, что допустимо ввиду их временного разнесения. Обозначив вероятности неблагоприятного воздействия при различных видах деятельности сил и средств ПСО верхними индексами подчеркнутых букв в соответствующих ключевых словах «поиск», «пере- ход» и «выполнение» видов деятельности сил и средств ПСО, получим следующее выражение:
PВВ = PП + PХ + PВ – PП ´ PХ – PП ´ PВ – – PХ ´ PВ + PП ´ PХ ´ PВ. (2)
Во-вторых, вычисление вероятностей PП, PХ и PВ для различных видов деятельности сил и средств ПСО проводить независимо (например, в соответствии с формулой (1)) для дальнейшего расчета PВВ.
Заметим, что в объеме представленных в таблице данных неблагоприятные технические факторы воздействуют только при поиске аварийных объектов. Если применить формулу (1) к PП как части PВВ в формуле (2), то для данного примера по всем видам деятельности при PП = 0.19, приняв PХ = PВ = 0.15 (условия малой видимости), получим следующее значение вероятности неблагоприятного внешнего воздействия на ход ПСД: PВВ = 0.19 + 2 ´ 0.15 – 2 ´ ´ 0.19 ´ 0.15 – 0.15 ´ 0.15 + 0.19 ´ 0.15 ´ 0.15 = = 0.41.
Очевидно, что при представленных в таблице и имеющих практическое значение существенно меньших единицы вероятностях в формуле (2) последнее слагаемое можно исключить. При этом для данного примера по-прежнему будет PВВ = 0.41.
В-третьих, при вычислении вероятностей PП, PХ и PВ для различных видов деятельности сил и средств ПСО предлагается перейти от весов в качестве поправочных коэффициентов к нечетким экспертным оценкам уровня воздействия неблагоприятных факторов. Последние позволяют вместо бинарных оценок неблагоприятных факторов, имеющих нерасчетный характер, использовать многозначные вербальные оценки.
Основоположник теории нечетких множеств Л. Заде отмечал, что во многих областях науки неточность и неопределенность обычно вводятся с помощью понятий и методов теории вероятности, в то время как во многих ситуациях источником неточности является не наличие каких-либо случайных величин, а появление классов, не имеющих строго определенных границ. Таковыми являются многие классы объектов реального мира. В этих случаях объект может принадлежать или не принадлежать к определенному классу, а также иметь промежуточные градации принадлежности, для описания которых необходимо использовать многозначную логику. Основное различие между случайностью и нечеткостью в том, что слу- чайность связана с неопределенностью принадлежности или непринадлежности объекта к четкому множеству, а нечеткость относится к классам с различными градациями степе- ни принадлежности объектов к данному классу [5].
Для перехода к нечетким экспертным оценкам в соответствии с содержанием таблицы введем лингвистические переменные воздействий неблагоприятных факторов, которые обозначим и поименуем следующим образом: F1 – снижение поисковой производительности сил поиска относительно расчетной; F2 – ночные условия; F3 – штормовые условия; F4 – условия малой видимости; F5 – неблагоприятная гидрология. При необходимости отнесения к различным видам деятельности сил и средств ПСО имена лингвистических переменных воздействий неблагоприятных факторов подобно вероятностям неблагоприятных воздействий дополняются такими же верхними индексами. Так, F3П означает «штормовые условия при поиске аварийных объектов», а F4Х – «условия малой видимости при переходе в район аварийных объектов».
Значениями лингвистических переменных являются поименованные нечеткие множества, определяемые функциями принадлежности, принимающими значения в диапазоне от 0 до 1. Каждая лингвистическая переменная имеет свой перечень значений (терм-множество). При определении терм-множеств будем руководствоваться известным положением о том, что человек в словесных оценках обычно не может различить больше трех, в лучшем случае – шести градаций. Соответственно, функция принадлежности, отражающая мнение одного человека, может быть определена лишь с точностью от 17 до 33 % [6].
Примем в качестве терм-множества лингвистической переменной F1 соответствующие значения непосредственно из таблицы. Для лингвистической переменной F2 примем достаточными всего два значения – «почти» и «полностью», конкатенирующиеся с именем лингвистической переменной. Для остальных лингвистических переменных примем терм-множества из трех значений: «легкие», «сложные» и «критические», конкатенирующиеся с именем соответствующей лингвистической переменной.
Приведенные в таблице значения весов для неблагоприятных факторов, не имеющих градаций, исходя из логики задания их величин, соотносим с воздействиями неблагоприятных факторов, существенно снижающими эффек- тивность ПСО. Таким образом, для лингвистической переменной F2 приведенное в таблице значение веса логично соотнести со значением «полностью ночные условия», в то время как значение «почти ночные условия» может быть наиболее характерно для позднего вечернего или предрассветного времени. Для остальных лингвистических переменных воздействий неблагоприятных факторов, не имеющих градаций, приведенные в таблице значения весов соотносим со значениями «сложные», конкатенирующиеся с именем соответствующей лингвистической переменной. При этом значения «легкие», как и значение «почти», отражают неполное воздействие соответствующего неблагоприятного фактора, а значения «критические» – максимально допустимое для прове- дения ПСД воздействие соответствующего неблагоприятного фактора. Первоначально принятые таким образом терм-множества в дальнейшем могут быть расширены при появлении информации, достаточной для расширения градаций воздействия неблагоприятных факторов и позволяющей с их введением повысить точность выполняемых вычислений.
Имена значений лингвистических переменных будем обозначать именами лингвистических переменных с нижним индексом их порядковых номеров в терм-множествах, например, F21 – «почти ночные условия», F33 – «критические штормовые условия». Поскольку некоторые неблагоприятные факторы могут воздействовать, в том числе по-разному, при нескольких видах деятельности сил и средств ПСО, обозначения имен значений лингвистических переменных, как и обозначения имен лингвистических переменных, могут содержать соответствующие уточняющие верхние индексы. Например, F3П1, F3Х2 и F3В2 означают «легкие штормовые условия при поиске аварийных объектов», «сложные штормовые условия при переходе в район аварийных объектов» и «сложные штормовые условия при выполнении задач ПСО в районе аварийных объектов» соответственно. В общем случае это будут три разных значения, поскольку одни и те же значения лингвистических переменных при различных видах деятельности сил и средств ПСО могут не совпадать. В случае идентичности одних и тех же значений лингвистических переменных при различных видах деятельности сил и средств ПСО, которые следуют из приведенных текущих значений в таблице, верхние индексы излишни. Так, выражение F3Х = F31 означает, что «штормовые усло- вия при переходе в район аварийных объек- тов» – «легкие штормовые условия», а выражение F3 = F31 – «легкие штормовые условия» при всех видах деятельности сил и средств ПСО.
Функция принадлежности μ(x) задает субъективную степень уверенности эксперта в том, что данное конкретное значение x базовой шкалы носителя (подмножества универсума, во всех точках которого функция принадлежности больше 0), на которой она определяется, соответствует определяемому этой функцией нечеткому множеству. Универсумом для значений введенных лингвистических переменных как нечетких множеств является диапазон от 0 до 1, значения в котором интерпретируются как ожидаемая степень воздействия соответствующего неблагоприятного фактора. Они задаются с точностью не выше 0.01 (см. таблицу). Основным классом методов построения функции принадлежности являются методы экспертных оценок. Естественные свойства функции принадлежности – это наличие одного максимума и гладкие, затухающие до нуля фронты [6].
Приведенные в таблице условные веса факторов будем использовать в качестве значений базовой шкалы носителя, при которых функции принадлежности соответствующих весам значений лингвистических переменных принимают значение 1, максимальное для нормализованных функций принадлежности. Такими значениями лингвистических переменных, как отмечалось выше, являются все значения лингвистической переменной F1, значение «полностью ночные условия» для лингвистической переменной F2 и значение «сложные», конкатенирующееся с именем соответствующей лингвистической переменной, для остальных лингвистических переменных. Обозначив для i-го значения N-й лингвистической переменной значение базовой шкалы носителя, при котором функция принадлежности принимает значение 1, как M(FNi), из таблицы непосредственно получим: M(F11) = 0.05, M(F12) = 0.10, M(F13) = 0.20, M(F22) = 0.07, M(F32) = 0.15, M(F42) = 0.15, M(F52) = 0.20. Ввиду упоря- доченности значений лингвистических переменных в терм-множествах для любых i < j должно выполняться M(FNi) < M(FNj). Величины M(FNi) остальных значений лингвистических переменных, не получаемых непосредственно из таблицы, а также виды самих функций принадлежности могут отличаться для различных реализаций предлагаемого подхода.
После полного определения всех значений лингвистических переменных (то есть построения их функции принадлежности) экспертный выбор значений лингвистических переменных воздействий неблагоприятных факторов, которые действуют в условиях конкретных ПСД, служит исходными данными для вычисления вероятностей PП, PХ и PВ для различных видов деятельности сил и средств ПСО. При этом используются дефаззификации выбранных экспертами нечетких множеств – значений лингвистических переменных воздействий неблагоприятных факторов. Дефаззификация – преобразование нечеткого множества в наиболее соответствующее по определенному критерию его четкое представление – в зависимости от контекста выполняемой задачи осуществляется различными методами. Среди наиболее распространенных методов дефаззификации – метод центра тяжести композиции максимум-минимум в результате логического вывода, метод медианы (среднего значения), метод весов (максимального значения принадлежности), крайние максимумы (самое левое или самое правое значение с максимальным значением принадлежности) [7]. При выборе метода учитывается то, что семантика операций над нечеткими множествами сильно зависит от контекста [8, 9]. В данном случае наиболее адекватными представляются метод весов при однозначном экспертном выборе и метод медианы, когда экспертно указываются несколько значений лингвистических переменных.
Реализация предлагаемого нечеткого подхода и контрольный пример
Для полного определения всех значений лингвистических переменных воздействий неблагоприятных факторов необходимо определить величины M(FNi) значений лингвистических переменных, не получаемых непосредственно из таблицы, а также виды самих функций принадлежности для всех значений лингвистических переменных. При этом возможен широкий диапазон различных реализаций. Однако их оптимизация каким-либо классическим способом, например, минимизацией среднеквадратической ошибки между заданными исходными значениями и значениями аппроксимирующей нечеткой модели, в данном случае невозможна, так как требует количества контрольных данных, нереальных в данном контексте. Поэтому предлагается следующая эвристическая реализация рассмотренного нечеткого подхода.
При определении M(FNi), N = 2..5, будем исходить из предположений о равноудаленности смежных градаций словесных оценок человеком и о равенстве нулю значения на базовой шкале носителя при отсутствии воздействия неблагоприятных факторов. Из этих предположений следует, что максимумы функции принадлежности значений лингвистических переменных, отражающих неполное воздействие неблагоприятных факторов и предшествующих в терм-множествах лингвистических переменных значениям, определяемым непосредственно из таблицы, располагаются на базо- вой шкале носителя посредине между 0 и этими значениями. Таким образом, получаем: M(F21) = 0.04, M(F31) = 0.08, M(F41) = 0.08, M(F51) = 0.10. Для лингвистических переменных F3, F4 и F5, имеющих в их терм-множествах критические значения, следующие за определяемыми непосредственно из таблицы сложными значениями, получаем: M(F33) = = 0.22, M(F43) = 0.22, M(F53) = 0.30.
Учитывая небольшой объем исходных данных в виде таблицы, в качестве функций принадлежности будем использовать широко распространенные нормированные (с единичным максимумом) треугольные функции, отличающиеся простотой и наглядностью в сочетании с достаточной в данных условиях точностью. Их вершины определяются значениями величин M(FNi) на базовой шкале носителя. При определении границ затухающих до нуля фронтов функции принадлежности исходим из того, что при таком небольшом количестве градаций словесных оценок одно и то же значение на базовой шкале носителя может относиться не более чем к двум смежным термам лингвистических переменных. Полагая построение функции принадлежности всех термов лингвистических переменных по одинаковым правилам, получаем, что их фронты не должны выходить за значения носителя максимумов функции принадлежности смежных термов. Принадлежность любого значения на базовой шкале носителя между вершинами функции принадлежности к обоим смежным термам лингвистических переменных достигается при совпадении значения носителя фронта и максимума смежных термов лингвистических переменных. При таком построении фронтов функции принадлежности в случае треугольных функций принадлежности получаем равную единице сумму значений принадлежностей для каждого значения носителя нечеткого множества этой лингвистической переменной в области пересечения ее термов. Следствием этого свойства является простой характер графиков дефаззификации экспертного выбора значений лингвистических переменных воздействий неблагоприятных факторов. Для крайних термов лингвистических переменных ширина фронта функции принадлежности со стороны отсутствия смежных термов принимается равной ширине другого фронта этого же терма, при этом левым фронтом левого терма всегда будет значение 0 на базовой шкале носителя. Графики построенных таким образом функций принадлежности термов лингвистических переменных приведены на рисунке 1.
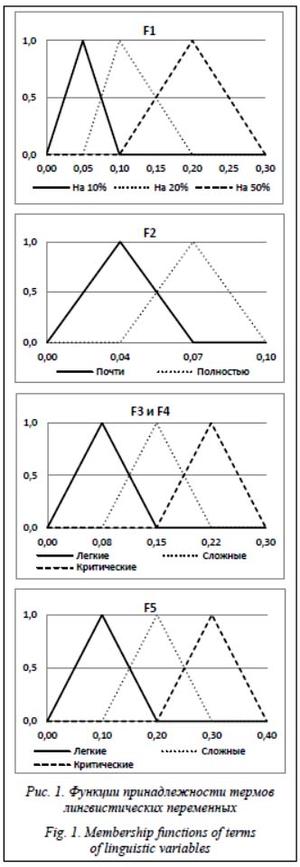
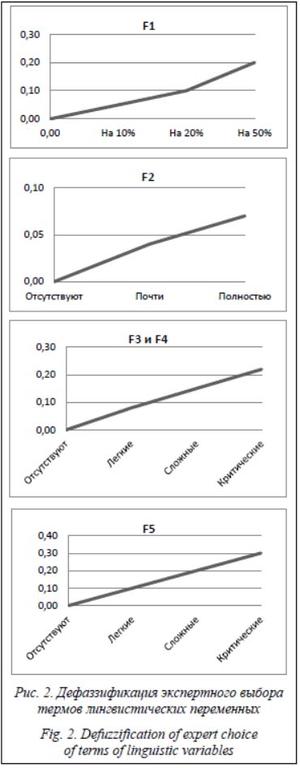 Упомянутая особенность равенства единице суммы значений принадлежностей для каждого значения носителя в области пересечения значений лингвистических переменных позволяет графически просто реализовать дефаззификацию – четкое представление экспертного выбора значения лингвистической переменной. Экспертная оценка ожидаемой степени воздействия соответствующего неблагоприятного фактора на таком графике откладывается по оси ординат, а по оси абсцисс равномерно размещаются упорядоченные значения лингвистических переменных (элементы ее терм-множества). График представляет собой ломаную линию, соединяющую точки максимумов соответствующих значений лингвистических переменных. На рисунке 2 приведены графики дефаззификации экспертного выбора значений лингвистических переменных.
Упомянутая особенность равенства единице суммы значений принадлежностей для каждого значения носителя в области пересечения значений лингвистических переменных позволяет графически просто реализовать дефаззификацию – четкое представление экспертного выбора значения лингвистической переменной. Экспертная оценка ожидаемой степени воздействия соответствующего неблагоприятного фактора на таком графике откладывается по оси ординат, а по оси абсцисс равномерно размещаются упорядоченные значения лингвистических переменных (элементы ее терм-множества). График представляет собой ломаную линию, соединяющую точки максимумов соответствующих значений лингвистических переменных. На рисунке 2 приведены графики дефаззификации экспертного выбора значений лингвистических переменных.
Заранее подготовленные графики дефаззификации экспертного выбора значений лингвистических переменных воздействий неблагоприятных факторов позволяют оперативно получать четкие оценки уровня воздействия неблагоприятных факторов, обозначаемые для лингвистической переменной FN как E(FN). Предположим, что для рассматриваемого примера экспертный выбор условий малой видимости при поиске аварийных объектов располагается значительно ближе к сложным, чем к легким, при переходе в район аварийных объектов – посредине между сложными и легким, а при выполнении задач ПСО в районе аварийных объектов – к легким. Тогда по приведенному на рисунке 2 графику можно получить, что E(F4П) = 0.13, E(F4Х) = 0.11, E(F4В) = 0.08. Соответственно, PХ = 0.11, PВ = 0.08 и по фор- муле (1) для PП получим: PП = 0.05 + 0.13 – – 0.05 ´ 0.13 = 0.17. В результате по формуле (2) без рассмотрения последнего слагаемого имеем: PВВ = 0.17 + 0.11 + 0.08 – 0.17 ´ 0.11 – – 0.17 ´ 0.08 – 0.11 ´ 0.08 = 0.32.
 Если при выполнении задач ПСО в районе аварийных объектов к легким условиям малой видимости добавятся легкие штормовые условия (E(F3В) = 0.08), то при предположении попарной независимости неблагоприятных факторов аналогично формулам (1) и (2) величина PВ составит: PВ = 0.08 + 0.08 – 0.08 ´ 0.08 = 0.15. В результате PВВ составит: PВВ = 0.17 + 0.11 + + 0.15 – 0.17 ´ 0.11 – 0.17 ´ 0.15 – 0.11 ´ 0.15 = = 0.37.
Если при выполнении задач ПСО в районе аварийных объектов к легким условиям малой видимости добавятся легкие штормовые условия (E(F3В) = 0.08), то при предположении попарной независимости неблагоприятных факторов аналогично формулам (1) и (2) величина PВ составит: PВ = 0.08 + 0.08 – 0.08 ´ 0.08 = 0.15. В результате PВВ составит: PВВ = 0.17 + 0.11 + + 0.15 – 0.17 ´ 0.11 – 0.17 ´ 0.15 – 0.11 ´ 0.15 = = 0.37.
 Наконец, при уточнении условных весов в таблице, например, на основе результатов проведения специальных учений сил ПСО ВМФ, соответствующим образом изменяются графики функции принадлежности термов лингвистических переменных и дефаззификации экспертного выбора термов лингвистических переменных. Так, если условный вес условий малой видимости при переходе в район аварийных объектов уменьшится с 0.15 до 0.12 при неизменных остальных условных весах, то потребуется построение отдельных графиков для F4Х, приведенных на рисунке 3. В этом случае в рассматриваемом примере величина PХ вместо 0.11 будет равна 0.09 и, соответственно, PВВ вместо 0.37 станет равно 0.36.
Наконец, при уточнении условных весов в таблице, например, на основе результатов проведения специальных учений сил ПСО ВМФ, соответствующим образом изменяются графики функции принадлежности термов лингвистических переменных и дефаззификации экспертного выбора термов лингвистических переменных. Так, если условный вес условий малой видимости при переходе в район аварийных объектов уменьшится с 0.15 до 0.12 при неизменных остальных условных весах, то потребуется построение отдельных графиков для F4Х, приведенных на рисунке 3. В этом случае в рассматриваемом примере величина PХ вместо 0.11 будет равна 0.09 и, соответственно, PВВ вместо 0.37 станет равно 0.36.
Любое изменение условных весов, детализация или расширение таблицы требуют перестроения графиков функций принадлежности термов и дефаззификации экспертного выбора термов лингвистических переменных перед их применением. Однако, поскольку существуют эффективные способы хранения и обработки нечетких данных [10], автоматизация как перестроения, так и применения этих графиков, аналитически представляемых кусочно-линейными функциями, совместно с выражениями вида (1) и (2) в реальном времени решения задачи прогнозирования эффективности различных возможных (наиболее вероятных) вариантов ПСД для выбора наиболее эффективного варианта не представляют сложностей. Рассмотренная реализация предлагаемого нечеткого подхода позволяет организовать эргономичный интерфейс автоматизированного рабочего места, в котором на экране под графиками дефаззификации экспертного выбора значений воздействий неблагоприятных факторов при различных видах деятельности сил и средств ПСО отображаются подвижные бегунки для установки оценки вероятности неблагоприятного внешнего воздействия на ход ПСД. Значение оценки пересчитывается при каждом перемещении оператором (экспертом) бегунка вдоль горизонтальной оси любого графика вербальной оценки воздействия неблагоприятных факторов. При наличии нескольких экспертов их мнения, если они различаются, могут быть сведены к общему мнению применением, например, метода Дельфи с контролем отклонения от единицы значения дисперсионного коэффициента конкордации [11].
Заключение
Таким образом, подход с использованием нечетких экспертных оценок воздействия неблагоприятных факторов на эффективность ПСО и его реализация позволяют в значительной мере преодолеть основные проблемы существующей методики оценки эффективности ПСО при определении одного из важнейших ее показателей – вероятности неблагоприятного внешнего воздействия на ход ПСД. Устранена неоднозначность методики в случае различных условных весов одного и того же неблагоприятного фактора при различных видах деятельности сил и средств ПСО и при одновременном воздействии нескольких неблагоприятных факторов в рамках одного вида деятельности. Введением лингвистических переменных воздействий неблагоприятных факторов и определением их терм-множеств преодолена грубость оценки эффективности ПСО из-за отсутствия градаций воздействия большинства неблагоприятных факторов. Обусловленная малым объемом контрольных данных предложенная эвристическая реализация нечеткого подхода с минимальными терм-множествами и треугольными функциями принадлежности введенных лингвистических переменных позволяет получать приемлемый результат в условиях ограниченных исходных данных. Она предоставляет возможность улучшения оценки эффективности ПСО при возможных корректировках, расширениях и дополнениях содержания таблицы с условными весами на основе результатов проведения специальных учений сил ПСО ВМФ.
Предлагаемые подход к оценке эффективности ПСО и его реализация могут служить основой для дальнейшей разработки методов оценки эффективности ПСО с более гибким учетом воздействия неблагоприятных факторов, например, создания системы нечеткого вывода.
Литература
1. The New Zealand Search and Rescue Strategic Plan 2017–2020. URL: https://nzsar.govt.nz/Portals/4/ Publications/NZSAR%20Strategic%20Documents/NZSAR%20Strategic%20Plan%202017-20.pdf (дата обращения: 01.08.2019).
2. National Search and Rescue Plan of the United States. 2007. URL: https://www.hsdl.org/?view&did= 481626 (дата обращения: 01.08.2019).
3. Norrington L., Quigley J., Russell A., Van der Meer R. Modelling the reliability of search and rescue operations with Bayesian Belief Networks. Reliab. Eng. Syst. Safe., 2008, vol. 93, iss. 7, pp. 940–949. DOI: 10.1016/j.ress.2007.03.006.
4. Abi-Zeida I., Frost J.R. SARPlan: A decision support system for Canadian Search and Rescue Operations. EJOR, 2005, vol. 162, iss. 3, pp. 630–653. DOI: 10.1016/j.ejor.2003.10.029.
5. Zadeh L.A. Fuzzy Sets. Information and Control, 1965, vol. 8, pp. 338–353. DOI: 10.2307/2272014.
6. Орлов А.И., Луценко Е.В. Системная нечеткая интервальная математика. Краснодар: Изд-во КубГАУ, 2014. 600 с.
7. Асаи К., Ватада Д., Иваи С. Прикладные нечеткие системы; [пер. с япон. Ю.Н. Чернышова]. М.: Мир, 1993. 368 с.
8. Поспелов Д.А. «Серые» и/или «черно-белые» [шкалы] // Прикладная эргономика. 1994. № 1. С. 29–33.
9. Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений; [пер. с англ. Н.И. Ринго]. М.: Мир, 1976. 165 с.
10. Сорокин В.Е. Хранение и эффективная обработка нечетких данных в СУБД PostgreSQL // Программные продукты и системы. 2017. Т. 30. № 4. С. 5–14. DOI:10.15827/0236-235X.120.609-618.
11. Оразбаев Б.Б. Экспертные системы для медицинской диагностики с применением методов теории нечетких множеств // ИТпортал. 2016. № 4. URL: http://itportal.ru/science/tech/ekspertnye-sistemy-dlya-meditsinsko/ (дата обращения: 01.02.2019).
References
- The New Zealand Search and Rescue Strategic Plan 2017–2020. Available at: https://nzsar.govt.nz/Portals/4/Publications/NZSAR%20Strategic%20Documents/NZSAR%20Strategic%20Plan%202017-20.pdf (accessed August 01, 2019).
- National Search and Rescue Plan of the United States. 2007. URL: https://www.hsdl.org/?view&did=481626 (accessed August 01, 2019).
- Norrington L., Quigley J., Russell A., Van der Meer R. Modelling the reliability of search and rescue operations with Bayesian Belief Networks. Reliab. Eng. Syst. Safe. 2008, vol. 93, iss. 7, pp. 940–949. DOI: 10.1016/j.ress.2007.03.006.
- Abi-Zeida I., Frost J.R. SARPlan: A decision support system for Canadian Search and Rescue Operations. EJOR, 2005, vol. 162, iss. 3, pp. 630–653. DOI: 10.1016/j.ejor.2003.10.029.
- Zadeh L.A. Fuzzy Sets. Information and Control, 1965, vol. 8, pp. 338–353. DOI: 10.2307/2272014.
- Orlov A.I., Lutsenko E.V. Systemic Fuzzy Interval Mathematics. Krasnodar, Kuban SAU Publ., 2014, 600 p. (in Russ.).
- Asai K., Watada D., Iwai S. Applied Fuzzy Systems. T. Tara, K. Asai, M. Sugeno (Eds.). Tokyo, Ohmsha Publ., 1989. Rus. ed.: Moscow, Mir Publ., 1993, 368 p.
- Pospelov D.A. “Gray” and / or “black and white” [scales]. Applied Ergonomics. 1994, no. 1, pp. 29–33 (in Russ.).
- Zadeh L.A. The concept of a linguistic variable and its application to approximate reasoning. In: Fu K.S., Tou J.T. (eds) Learning Systems and Intelligent Robots. Springer, Boston, MA, 1974. DOI: 10.1007/978-1-4684-2106-4_1. Rus. ed.: Moscow, Mir Publ., 1976, 165 p.
- Sorokin V.E. Fuzzy data storing and efficient processing in PostgreSQL DBMS. Software and Systems, 2017, vol. 30, no. 4, pp. 5–14. DOI:10.15827/0236-235X.120.609-618.
- Orazbaev B.B. Expert systems for medical diagnostics using fuzzy set theory methods. Itportal, 2016, no. 4. Available at: http://itportal.ru/science/tech/ekspertnye-sistemy-dlya-meditsinsko/ (accessed August 01, 2019).







