Оптимизация тепломассопереноса в технологических процессах связана с взаимодействием потока вещества со стенками систем [1–3]. Особый интерес представляет исследование процесса тепломассопереноса в наноразмерных системах [4–6], когда число Кнудсена больше единицы. На микроскопическом уровне испарение вещества с поверхности конденсированной фазы связано с взаимодействием вылетающих молекул с молекулами конденсированной фазы и с другими молекулами, вылетевшими с поверхности конденсированной фазы [7–9]. Возможен аналог образования слоя Кнудсена при испарении вещества [10–12]. В этом слое практически нет столкновений вылетающих с поверхности конденсированной фазы атомов друг с другом [13–15]. При слабоинтенсивном испарении вещества с поверхности конденсированной фазы атомы или молекулы могут пролететь достаточно большое расстояние до взаимного столкновения [16–18].
В данной работе на основе компьютерного эксперимента методом Монте-Карло проведен анализ распределений столкновений двух атомов над поверхностью, вылетевших с ограниченного участка поверхности конденсированной фазы. Метод Монте-Карло достаточно часто используется при численном моделировании различных физических систем. При этом достоверность результатов во многом обусловлена количеством сгенерированных и обработанных вариантов, что делает нецелесообразным использование последовательных вычислений на CPU из-за высоких затрат времени на проведение эксперимента.
Одним из способов повышения производительности является использование параллельных вычислений. Новый подход к рассматриваемой физической задаче и соответствующая модель процесса испарения потребовали разработки нового параллельного алгоритма и ПО. Одним из наиболее доступных вариантов орга- низации параллельных вычислений является использование GPU c архитектурой CUDA. Важным фактором при выборе вычислительной платформы послужило распараллеливание задачи по данным, что полностью соответствует специфике организации вычислений на графических процессорах. Это позволило создать программу, эффективно решающую задачу моделирования процесса испарения и получения распределений столкновений двух атомов, и получить достоверные статистические данные.
Параллельный алгоритм моделирования столкновений двух атомов
В процессе испарения с поверхности выле- тает большое количество атомов с различными скоростями, часть которых сталкиваются друг с другом. Закон движения для каждого атома зависит только от начальных данных (координат на поверхности и скорости). Очевидно, что можно производить вычисления для нескольких пар атомов одновременно, то есть инструкции будут одинаковыми, а данные разными. Другими словами, задача относится к классу SIMD (Single Instruction stream/Multiple Data stream) и алгоритм может быть адаптирован к эффективным вычислениям на графических процессорах с технологией CUDA (Compute Unified Device Architecture) [19].
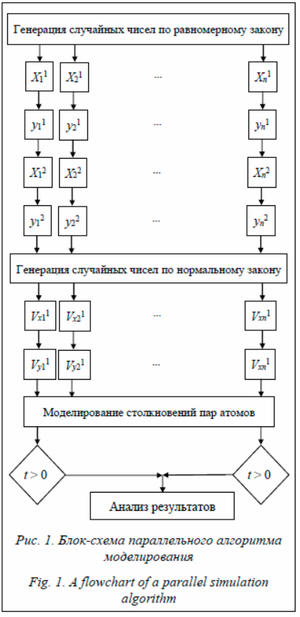 Блок-схема параллельного алгоритма моделирования столкновений атомов, вылетевших с поверхности конденсированной фазы, представлена на рисунке 1.
Блок-схема параллельного алгоритма моделирования столкновений атомов, вылетевших с поверхности конденсированной фазы, представлена на рисунке 1.
Программная реализация выполнена на языке С++ с использованием набора расширений для графических процессоров Nvidia с архитектурой CUDA. Для генерации значений случайных величин использовались библиотека CURAND и генераторы чисел, распределенных по нормальному и равномерному законам. Приведем пример заполнения массива случайными числами в параллельном режиме:
#include
#include
…
cudaMalloc((void**)& devX1, CHH * sizeof(double));
cudaMalloc((void**)& devVX1, CHH * sizeof(double));
curandGenerator_t gen;
curandCreateGenerator(&gen, CURAND_RNG_PSEUDO_DEFAULT);
curandSetPseudoRandomGeneratorSeed(gen, 1234ULL);
curandGenerateUniformDouble(gen, devX1, CHH);
curandGenerateNormalDouble(gen, devVX1, CHH, m, sigma);
…
cudaMemcpy(ptrX1, devX1, CHH * sizeof(double), cudaMemcpyDeviceToHost);
cudaMemcpy(ptrVX1, devVX1, CHH * sizeof(double), cudaMemcpyDeviceToHost);
Каждый компьютерный эксперимент проводился до тех пор, пока не разыгрывалось более 300 млн столкновений пар атомов. Так, 1 200 692 724 столкновений произошло за 19.34 сек., 2101667707 – за 34.4 сек., 6303823665 – за 100.47 сек. Точность полученных результатов меньше нескольких сотых процента. Для каждой пары атомов разыгрывались их положения (х1, у1) и (х2, у2) на ограниченном участке поверхности конденсированной фазы со стороной a = 3∙10-9 м (в базовом варианте) и компоненты скоростей этих атомов (vx1, vy1, vz1) и (vx2, vy2, vz2) в плоскости z = 0. В модели жестких сфер предполагалось, что атомы имеют вид сфер с радиусом r = 1,5∙10-10 м и массой m = 40 а.е.м.
Вычисления производились на гетерогенной платформе HybriLIT, состоящей из суперкомпьютера «Говорун» и учебно-тестового полигона HybriLIT. Данная платформа является частью многофункционального информационно-вычислительного комплекса лаборатории информационных технологий Объединенного института ядерных исследований, г. Дубна [20]. Для моделирования процесса столкновений атомов, вылетевших с поверхности конденсированной фазы, использовался ускоритель NVIDIA Tesla K80 (4 992 ядра CUDA на карте с двумя GPU, производительность в операциях с двойной точностью до 2,91 терафлопса) [21].
Как видно из результатов эксперимента, при значительном увеличении количества столкновений (соответственно, и разыгранных пар атомов, вылетевших с поверхности конденсированной фазы) фактическое время выполнения растет линейно. Адаптация алгоритма к параллельным вычислениям позволила смоделировать процесс вылета для увеличенных размеров области испарения и выявить зависимости от размера этой площади.
Результаты расчетов
В данной работе представлены результаты расчетов распределения столкновений двух атомов, вылетевших с ограниченной поверхности конденсированной фазы, в зависимости от размера области испарения а и температуры поверхности конденсированной фазы Т.
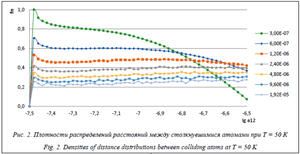 На рисунке 2 представлены результаты расчетов нормированных плотностей распределений расстояний между атомами на поверхности конденсированной фазы a12, столкнувшимися над поверхностью. Минимальное расстояние равно диаметру атомов, а максимальное – положению атомов в противоположных углах области испарения.
На рисунке 2 представлены результаты расчетов нормированных плотностей распределений расстояний между атомами на поверхности конденсированной фазы a12, столкнувшимися над поверхностью. Минимальное расстояние равно диаметру атомов, а максимальное – положению атомов в противоположных углах области испарения.
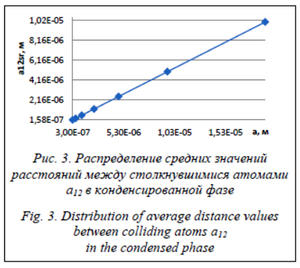
Распределение средних расстояний между столкнувшимися атомами в зависимости от размера области испарения показано на рисунке 3. Установлено, что средние расстояния увеличиваются линейно с увеличением размера области испарения. Необходимо отметить: как плотности распределений, так и сред- ние значения расстояний а12 не зависят от температуры конденсированной фазы Т. Это можно объяснить тем, что положения атомов на поверхности конденсированной фазы разыгрывались с помощью датчика равномерно распределенных случайных величин. С физической точки зрения это означает, что интенсивность испарения уменьшается.
 Проведенные компьютерные эксперименты показали, что плотности распределений столкновений над поверхностью конденсированной фазы (z = 0) не зависят от температуры конденсированной фазы Т. Величина z определялась как расстояние от поверхности конденсированной фазы до точки столкновения атомов. Это можно объяснить тем, что температура поверхности определяет средние скорости атомов, влияющие на время до столкновения атомов, но не на геометрию расстояния до столкновения.
Проведенные компьютерные эксперименты показали, что плотности распределений столкновений над поверхностью конденсированной фазы (z = 0) не зависят от температуры конденсированной фазы Т. Величина z определялась как расстояние от поверхности конденсированной фазы до точки столкновения атомов. Это можно объяснить тем, что температура поверхности определяет средние скорости атомов, влияющие на время до столкновения атомов, но не на геометрию расстояния до столкновения.
Аналогичный вид имеет и плотность распределения длин пробега атомов до столкновения l. Данная величина определялась как квадратный корень из суммы квадратов проекций перемещений первого атома на оси координат.
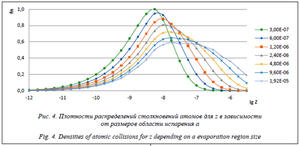
Плотности распределений столкновений над поверхностью конденсированной фазы z в зависимости от стороны области испарения а отражены на рисунке 4. С увеличением размера области испарения плотности распределений и максимумы распределений смещаются в область больших значений z. Плотности распределений становятся более пологими, а максимумы распределений уменьшаются по ве- личине. Это можно объяснить тем, что рас- стояния между сталкивающимися атомами на поверхности конденсированной фазы с увеличением области испарения растут.
 Следует отметить, что кривые плотностей распределений для величины l на графике (см. http://www.swsys.ru/uploaded/image/2020-2/202 0-2-dop/20.jpg) выглядят так же, как и для плотности распределения величины z. С увеличением размера области испарения а увеличиваются не только расстояния до столкновения атомов над поверхностью, но и проекции пробегов атомов по осям Ox и Oy. Вследствие этого соответствующие максимумы для величины l сдвинуты вправо по отношению к максимумам величины z.
Следует отметить, что кривые плотностей распределений для величины l на графике (см. http://www.swsys.ru/uploaded/image/2020-2/202 0-2-dop/20.jpg) выглядят так же, как и для плотности распределения величины z. С увеличением размера области испарения а увеличиваются не только расстояния до столкновения атомов над поверхностью, но и проекции пробегов атомов по осям Ox и Oy. Вследствие этого соответствующие максимумы для величины l сдвинуты вправо по отношению к максимумам величины z.
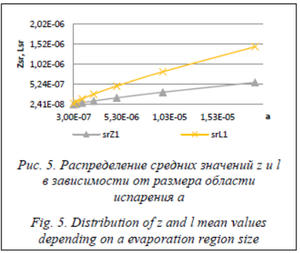
Представляет интерес получение распределений средних величин z и l в зависимости от размеров области испарения а. Установлено, что от температуры поверхности средние значения z не зависят, так как они связаны с плотностями распределений z, которые также не зависят от температуры. Зависимость средних значений z и l от размеров области испарения а показана на рисунке 5. Получены линейные зависимости от размеров области испарения а. Необходимо отметить, что с увеличением области испарения более чем в 60 раз максимумы распределений, а соответственно, и средние значения, увеличиваются только на порядок.
Заключение
Полученные в компьютерных экспериментах результаты расчетов позволили установить закономерности распределений столкновений двух вылетевших атомов над поверхностью конденсированной фазы. Установлено, что плотности распределений имеют сложную структуру, которая только через средние значения может быть связана с определением слоя Кнудсена. Получить данные результаты удалось благодаря использованию параллельных вычислений на графических процессорах nVidia и адаптации алгоритма расчета столкновений атомов к архитектуре CUDA.
Литература
1. Lee J., Laoui T., Karnik R. Nanofluidic transport governed by the liquid/vapour interface. Nat. Nanotechnol., 2014, vol. 9, pp. 317–323. DOI: 10.1038/nnano.2014.28.
2. Li Y., Alibakhshi M.A., Zhao Y., Duan C. Exploring ultimate water capillary evaporation in nanoscale conduits. Nano Lett., 2017, vol. 17, pp. 4813–4819.
3. Wilke K.L., Barabadi B., Lu Z., Zhang T., Wang E.N. Parametric study of thin film evaporation from nanoporous membranes. Appl. Phys. Lett., 2017, vol. 111, iss. 17, art. 171603. DOI: 10.1063/1.4997945.
4. Xiao R., Maroo S.C., Wang E.N. Negative pressures in nanoporous membranes for thin film evaporation. Appl. Phys. Lett., 2013, vol. 102, iss. 12, art. 123103. DOI: 10.1063/1.4798243.
5. Lu Z., Narayanan S., Wang E.N. Modeling of evaporation from nanopores with nonequilibrium and nonlocal effects. Langmuir, 2015, vol. 31, pp. 9817–9824.
6. Frezzotti A. Boundary conditions at the vapor-liquid interface. Phys. Fluids, 2011, vol. 23, iss. 3, art. 030609. DOI: 10.1063/1.3567001.
7. Persad A.H., Ward C.A. Expressions for the evaporation and condensation coefficients in the Hertz-Knudsen relation. Chem. Rev., 2016, vol. 116, pp. 7727–7767.
8. Knudsen M. Die maximale verdampfungsgeschwindigkeit des quecksilbers. Ann. Phys., 1915, vol. 352, pp. 697–708.
9. Tcheremissine F.G. Solution to the Boltzmann kinetic equation for high-speed flows. Comput. Math. Phys., 2006, vol. 46, pp. 315–329.
10. Ishiyama T., Fujikawa S., Kurz T., Lauterborn W. Nonequilibrium kinetic boundary condition at the vapor-liquid interface of argon. Phys. Rev. E, 2013, vol. 88, iss. 4, art. 042406. DOI: 10.1103/PhysRevE.88. 042406.
11. Kon M., Kobayashi K., Watanabe M. Liquid temperature dependence of kinetic boundary condition at vapor-liquid interface. Int. J. Heat Mass Transfer, 2016, vol. 99, pp. 317–326.
12. Cheng S., Lechman J.B., Plimpton S.J., Grest G.S. Evaporation of Lennard-Jones fluids. J. Chem. Phys., 2011, vol. 134, iss. 22, art. 224704. DOI: 10.1063/1.3595260.
13. Kon M., Kobayashi K., Watanabe M. Method of determining kinetic boundary conditions in net evaporation/condensation. Phys Fluids, 2014, vol. 26, iss. 7, art. 072003. DOI: 10.1063/1.4890523.
14. Kon M., Kobayashi K., Watanabe M. Kinetic boundary condition in vapor-liquid two-phase system during unsteady net evaporation/condensation. Eur. J. Mech.-B/Fluids, 2017, vol. 64, pp. 81–92. DOI: 10.1016/j.euromechflu.2016.12.001.
15. Kobayashi K., Sasaki K., Kon M., Fujii H., Watanabe M. Kinetic boundary conditions for vapor-gas binary mixture. Microfluid Nanofluid, 2017, vol. 21. DOI: 10.1007/s10404-017-1887-6.
16. Уварова Л.А., Плетнев Л.В. Компьютерное моделирование столкновений частиц при вылете с поверхности конденсированной фазы // Тр. ИСА РАН. Динамика неоднородных систем. 2008. Т. 32. С. 131–139.
17. Уварова Л.А., Плетнев Л.В. Распределения столкновений частиц при вылете с поверхности конденсированной фазы // Вестн. Поморского ун-та: Естественные науки. 2009. Т. 3. С. 102–107.
18. Плетнев Л.В. Распределения бинарных столкновений атомов при вылете с поверхности конденсированной фазы // Вестн. ТГТУ. 2011. Т. 17. Вып. 2. С. 520–524.
19. Желтов С.А. Особенности адаптации вычислительных алгоритмов к архитектуре CUDA // Математические методы управления: сб. науч. тр. ТГТУ. 2011. С. 33–36.
20. Гетерогенная платформа HybriLIT. URL: http://hlit.jinr.ru (дата обращения: 02.03.2020).
21. NVIDIA Tesla K80. URL: https://www.nvidia.com/ru-ru/data-center/tesla-k80 (дата обращения: 01.04.2020).
References
- Lee J., Laoui T., Karnik R. Nanofluidic transport governed by the liquid/vapour interface. Nat. Nanotechnol., 2014, vol. 9, pp. 317–323. DOI: 10.1038/nnano.2014.28.
- Li Y., Alibakhshi M.A., Zhao Y., Duan C. Exploring ultimate water capillary evaporation in nanoscale conduits. Nano Lett., 2017, vol. 8, no. 17, pp. 4813–4819.
- Wilke K.L., Barabadi B., Lu Z., Zhang T., Wang E.N. Parametric study of thin film evaporation from nanoporous membranes. Appl. Phys. Lett., 2017, vol. 111, iss. 17, art. 171603. DOI: 10.1063/1.4997945.
- Xiao R., Maroo S.C., Wang E.N. Negative pressures in nanoporous membranes for thin film evaporation. Appl. Phys. Lett., 2013, vol. 102, iss. 12, art. 123103. DOI: 10.1063/1.4798243.
- Lu Z., Narayanan S., Wang E.N. Modeling of evaporation from nanopores with nonequilibrium and nonlocal effects. Langmuir, 2015, vol. 31, pp. 9817–9824.
- Frezzotti A. Boundary conditions at the vapor-liquid interface. Phys. Fluids, 2011, vol. 23, iss. 3,
art. 030609. DOI: 10.1063/1.3567001.
- Persad A.H., Ward C.A. Expressions for the evaporation and condensation coefficients in the Hertz-Knudsen relation. Chem. Rev., 2016, vol. 116, pp. 7727–7767.
- Knudsen M. Die maximale verdampfungsgeschwindigkeit des quecksilbers. Ann. Phys., 1915, vol. 352, pp. 697–708.
- Tcheremissine F.G. Solution to the Boltzmann kinetic equation for high-speed flows. Comput. Math. Phys., 2006, vol. 46, pp. 315–329.
- Ishiyama T., Fujikawa S., Kurz T., Lauterborn W. Nonequilibrium kinetic boundary condition at the vapor-liquid interface of argon. Phys. Rev. E, 2013, vol. 88, iss. 4, art. 042406. DOI: 10.1103/PhysRevE.88.
042406.
- Kon M., Kobayashi K., Watanabe M. Liquid temperature dependence of kinetic boundary condition at vapor-liquid interface. Int. J. Heat Mass Transfer, 2016, vol. 99, pp. 317–326.
- Cheng S., Lechman J.B., Plimpton S.J., Grest G.S. Evaporation of Lennard-Jones fluids. J. Chem. Phys., 2011, vol. 134, iss. 22, art. 224704. DOI: 10.1063/1.3595260.
- Kon M., Kobayashi K., Watanabe M. Method of determining kinetic boundary conditions in net evaporation/condensation. Phys Fluids, 2014, vol. 26, iss. 7, art. 072003. DOI: 10.1063/1.4890523.
- Kon M., Kobayashi K., Watanabe M. Kinetic boundary condition in vapor-liquid two-phase system during unsteady net evaporation/condensation. Eur. J. Mech.-B/Fluids, 2017, vol. 64, pp. 81–92. DOI: 10.1016/j.euromechflu.2016.12.001.
- Kobayashi K., Sasaki K., Kon M., Fujii H., Watanabe M. Kinetic boundary conditions for vapor-gas binary mixture. Microfluid Nanofluid, 2017, vol. 21. DOI: 10.1007/s10404-017-1887-6.
- Uvarova L.A., Pletnev L.V. Computer simulation of particle collisions during departure from the surface of the condensed phase. Proc. ISA RAS. Dynamics of Inhomogeneous Systems, 2008, vol. 32,
pp. 131–139.
- Uvarova L.A., Pletnev L.V. Distributions of particle collisions at departure from the surface of the condensed phase. Bull. Pomeranian Univ. Ser. Natural Sciences, 2009, vol. 3, pp. 102–107.
- Pletnev L.V. Distributions of binary collisions of atoms at departure from the surface of the condensed phase. Bull. TSTU, 2011, vol. 17, iss. 2, pp. 520–524.
- Zheltov S.A. Features of adaptation of computational algorithms to the CUDA architecture. Proc. TSTU. Mathematical Methods of Management, 2011, pp. 33–36.
- Heterogeneous HybriLIT Platform. Avaible at: http://hlit.jinr.ru (accessed March 02, 2020).
- NVIDIA Tesla K80. Avaible at: https://www.nvidia.com/ru-ru/data-center/tesla-k80 (accessed April 01, 2020).








