Разработка автоматизированных средств описания производственных процессов является одной из перспективных технологий, позволяющих широко использовать опыт высококвалифицированных специалистов в предметной области. Для взаимодействия с экспертами создаются специальные предметно-ориентированные языки – Domain Specific Languages [1, 2], обеспечивающие использование понятных специалисту терминов и их автоматическую трансляцию в удобное для компьютерной обработки представление. Одним из универсальных предметно-ориентированных языков является методология функционального моделирования. По сравнению с другими средствами опи-сания предметной области существенными преимуществами функционального моделирования, с точки зрения эксперта, являются наглядность, возможность использования специалистами различного профиля, отсутствие ограничений на степень детализации [3, 4]. Средства формального представления функциональных моделей и их автоматизированного анализа обсуждаются в литературе значительно реже [5]. На рынке ПО представлен ряд коммерческих продуктов, в частности, AllFusion ERwin Data Modeler [6], Edraw [7], предназначенных для создания функциональных моделей. Однако в этих программных комплексах как формальный язык описания моделей, так и алгоритмы проверки правильности построения моделей скрыты от пользователя.
Таким образом, разработка алгоритмов и программ, предназначенных для верификации функциональных моделей, является актуальной научной задачей.
Алгоритм теоретико-множественного описания функциональных моделей
Первым этапом создания средств анализа функциональных моделей является разработка формального языка для их описания. В качестве основы для разработки такого языка предлагается использовать теорию графов: каждая диаграмма, входящая в функциональную модель, представляется в виде графа, а взаимосвязь между диаграммами задается с помощью отношения детализации на этих графах.
Классический граф состоит из двух множеств – вершин и дуг, причем каждая дуга представляет собой упорядоченную пару вершин. При использовании графов для описания функциональных моделей возникает вопрос, каким объектам поставить в соответствие вершины, а каким – дуги. Традиционно в теоретико-множественных моделях с помощью вершин описывают сущности, а с помощью дуг – отношения между ними. Но в функциональных моделях основными элементами являются именно функции, действия, а остальные объекты рассматриваются либо как аргументы, либо как результаты выполнения этих функций. Поэтому функциональным блокам поставим в соответствие вершины, а стрелкам – дуги графа. Отметим, что в функциональных моделях стрелки имеют метки, но теория графов допускает представление графов с помеченными дугами [8]. Кроме того, функциональные диаграммы имеют ряд особенностей, отличающих их от классических графов. Основные различия между функциональными диаграммами и графами приведены в таблице. Таким образом, для представления функциональной диаграммы в виде графа необходимо выполнить ряд дополнительных преобразований.
Для описания граничных стрелок множество вершин графа необходимо дополнить служебными вершинами, которые задают границы диаграммы и обозначаются латинскими буквами: L – левая, R – правая, U – верхняя, D – нижняя граница.
Положение стрелки относительно границ функционального блока задается указанием ролей вершин в системе ICOM. Роль расположена перед именем вершины и отделена от него двоеточием. Таким образом, каждая дуга графа в линейной нотации будет представлена следующим образом:
метка_стрелки(
роль_начальной_вершины:
имя_начальной_вершины,
роль_конечной_вершины:
имя_конечной_вершины).
Различия между функциональными диаграммами и графами
Differences between functional diagrams and graphs
|
Признак
|
Функциональная диаграмма
|
Граф
|
|
Граничные стрелки (стрелки, связывающие границы диаграммы и вершины)
|
Разрешены
|
Запрещены
|
|
Положение стрелки относительно границ функционального блока
|
Существенно
|
Несущественно
|
|
Ветвление стрелки
|
Разрешено
|
Запрещено
|
Для описания ветвящихся стрелок используются несколько дуг. В случае, если при ветвлении метка стрелки не изменяется, каждой ветви ставится в соответствие отдельная дуга. Метки всех этих дуг одинаковы. В противном случае необходимо добавить служебную вершину, задающую точку ветвления. Исходная стрелка и каждая ее ветвь задаются отдельными дугами графа.
Обобщенный алгоритм построения теоретико-множественного описания функциональной диаграммы приведен на рисунке 1. Рутинные процедуры, связанные с перебором всех объектов с заданными свойствами (например, всех функциональных блоков), в этом алгоритме реализованы в виде подпрограмм.
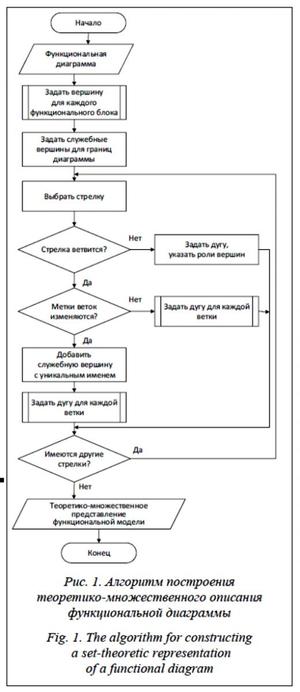 Функциональная модель представляет собой совокупность иерархически упорядоченных функциональных диаграмм. Отдельные диаграммы внутри одной модели связаны иерархическим отношением «от общего к частному» и могут быть представлены в виде дерева, корнем которого является диаграмма наивысшего уровня обобщения. Для теоретико-множественного представления этой иерархии используется отношение decompose, элементами которого являются упорядоченные тройки. Каждый элемент отношения включает в себя номер родительской (обобщенной) диаграммы, номер дочерней (детализированной) диаграммы, функциональный блок родитель-ской диаграммы, который детализируется с помощью дочерней диаграммы.
Функциональная модель представляет собой совокупность иерархически упорядоченных функциональных диаграмм. Отдельные диаграммы внутри одной модели связаны иерархическим отношением «от общего к частному» и могут быть представлены в виде дерева, корнем которого является диаграмма наивысшего уровня обобщения. Для теоретико-множественного представления этой иерархии используется отношение decompose, элементами которого являются упорядоченные тройки. Каждый элемент отношения включает в себя номер родительской (обобщенной) диаграммы, номер дочерней (детализированной) диаграммы, функциональный блок родитель-ской диаграммы, который детализируется с помощью дочерней диаграммы.
Формальные правила и алгоритм верификация функциональных моделей
Проверка правильности функциональной модели предполагает сопоставление стрелок, относящихся к заданному функциональному блоку родительской диаграммы, с граничными стрелками дочерней диаграммы. При этом роли стрелок должны сохраняться.
Для формализации правил верификации моделей [9] использованы следующие обозначения: DP = (NP, LP) – граф, задающий родительскую диаграмму, NP – множество вершин графа DP, LP – множество дуг графа DP; (DP, DC, nb) – элемент отношения decompose, который описывает декомпозицию блока nb родительской диаграммы, nb Î NP, DC = (NC, LC) – граф, задающий дочернюю диаграмму; NC – множество вершин графа DC, LC – множество дуг графа DC, np Î NP – элемент множества NP, np ¹ nb; nc Î NC – элемент множества NC.
Для стрелок родительской и дочерней диаграмм должны выполняться перечисленные далее соотношения.
· Каждой стрелке родительской диаграммы, которая входит в блок nb слева, на дочерней диаграмме должна соответствовать, по крайней мере, одна стрелка с той же меткой, которая выходит из левой границы диаграммы и указывает на какой-либо блок дочерней диаграммы слева:
если lp(O:np, I:nb) Î LP, то lp(O:L, I:nc) Î LC.
· Каждой стрелке родительской диаграммы, которая выходит из блока nb, на дочерней диаграмме должна соответствовать, по крайней мере, одна стрелка с той же меткой, которая входит в правую границу диаграммы из какого-либо блока дочерней диаграммы:
если lp(O:nb, I:np) Î LP, то lp(O:nc, I:R) Î LC.
· Каждой стрелке родительской диаграммы, которая входит в блок nb cверху, на дочерней диаграмме должна соответствовать, по крайней мере, одна стрелка с той же меткой, которая выходит из верхней границы диаграммы и указывает на какой-либо блок дочерней диаграммы сверху:
если lp(O:np, C:nb) Î LP, то lp(O:U, C:nc) Î LC.
· Каждой стрелке родительской диаграммы, которая входит в блок nb cнизу, на дочерней диаграмме должна соответствовать, по крайней мере, одна стрелка с той же меткой, которая выходит из нижней границы диаграммы и указывает на какой-либо блок дочерней диаграммы снизу:
если lp(O:np, M:nb) Î LP, то lp(O:D, M:nc) Î LC.
Вершины np и nc могут задавать как блоки соответствующих функциональных диаграмм, так и их границы или точки ветвления. Отметим также, что одной стрелке родительской диаграммы могут соответствовать несколько стрелок дочерней в том случае, если на дочерней диаграмме стрелка ветвится, но ее метка при этом не меняется.
 Алгоритм верификации функциональной модели для проверки этих правил приведен на рисунке 2.
Алгоритм верификации функциональной модели для проверки этих правил приведен на рисунке 2.
Применение средств логического программирования для верификации функциональных моделей
Для реализации алгоритма верификации функциональной модели подходят языки программирования, содержащие удобные средства описания и анализа отношений, а также средства сопоставления по образцу. Наиболее удобным представляется язык логического программирования Пролог, основанный на логике предикатов первого порядка [10]. К преимуществам этого языка относятся:
- декларативность (программа описывает требования к решению задачи, а не процедуру решения);
- простая и интуитивно понятная предикатная нотация, малое количество встроенных языковых объектов;
- развитые методы сопоставления по образцу, обеспечивающие удобство связывания переменных;
- встроенный автоматический поиск с возвратом, существенно упрощающий перебор объектов, подходящих под заданные условия.
При реализации алгоритма верификации функциональной модели использована свободно распространяемая программа SWI Prolog [11]. Ее важнейшим достоинством, помимо возможности свободного использования, является полное соответствие синтаксиса международному стандарту ISO [12].
Для хранения функциональной модели в языке Пролог потребуется база фактов, включающая три предиката: описание отношения детализации (decompose), множества вершин (node) и множества дуг (edge).
Факты, описывающие отношение детализации decompose, содержат три аргумента: имя родительской диаграммы, имя дочерней диаграммы, название функционального блока, который детализирован на дочерней диаграмме.
Факты, описывающие множество вершин node, содержат два аргумента: имя вершины и имя диаграммы, на которой находится эта вершина.
Факты, описывающие множество дуг edge, содержат пять аргументов: метка дуги, имя начальной вершины дуги, роль начальной вершины дуги, имя конечной вершины дуги, роль конечной вершины дуги.
В этих фактах для обозначения служебных вершин используются следующие константы: l – вершина, описывающая левую границу диаграммы; r – вершина, описывающая правую границу диаграммы; u – вершина, описывающая верхнюю границу диаграммы; d – вершина, описывающая нижнюю границу диаграммы; n0001, n0002… – вершины, описывающие узлы ветвления.
Для обозначения ролей используются следующие константы: о – выход (начало дуги), i – вход (конец дуги), c – управление, m – механизм.
Представим программу верификации функциональной модели:
edge_node(NB,[M,R]):-edge(M,R,NB,_,_).
edge_node(NB,[M,R]):-edge(M,_,_,R,NB).
list_edges(NB,L):-
findall(X, edge_node(NB, X), L).
rule(NB,[LP,i]):-decompose(DP, DC, NB),
edge(LP,o,NP,i,NB),edge(LP,o,l,i,NC),
node(NC,DC).
rule(NB,[LP,o]):-decompose(DP, DC, NB),
edge(LP,o,NB,i,NP),edge(LP,o,NC,i,r),
node(NC,DC).
rule(NB,[LP,c]):-decompose(DP, DC, NB),
edge(LP,o,NP,c,NB),edge(LP,o,u,c,NC),
node(NC,DC).
rule(NB,[LP,m]):-decompose(DP, DC, NB),
edge(LP,o,NP,m,NB),edge(LP,o,d,m,NC),
node(NC,DC).
verify_edges(NB,[]).
verify_edges(NB,[[M,R]|L]):-rule(NB,
[M,R]), verify_edges(NB,L).
verify_node(NB,L):-list_edges(NB, L),
verify_edges(NB,L).
list_nodes(DC,L):-
findall(X, decompose(DC, _, X),L).
verify_d([]).
verify_d([NB|LNB]):-verify_node(NB, _),
verify_d(LNB).
verify(DC):- list_nodes(DC, LN),veryfy_d(LN).
Проверка правильности построения функциональной модели выполняется с помощью предиката verify, аргументом которого является имя родительской функциональной диаграммы. Этот предикат имеет значение true, если модель построена правильно, и false в противном случае. Предикат вызывает предикат list_nodes, который по имени диаграммы формирует список входящих в нее функциональных блоков, и предикат verify_d, выполняющий проверку функциональных блоков из этого списка. Отметим, что при описании предиката list_nodes для построения списка элементов, удовлетворяющих заданному условию, используется встроенный предикат findall.
Для проверки отдельного блока используется предикат verify_node, входным аргументом которого является имя блока, а результатом – список проверенных стрелок. Этот предикат вызывает предикат list_edges, который по имени функционального блока находит список всех связанных с ним стрелок. В определении этого предиката также используется встроенный предикат findall. Условие «стрелка связана с функциональным блоком NB» задает предикат edge_node.
Предикат verify_edges выполняет последовательный перебор и проверку списка стрелок. Проверка отдельной стрелки выполняется с помощью предиката rule. Каждое правило этого предиката соответствует одному из правил верификации. Так, первое правило описывает соответствие между стрелками с ролью «вход». Переменные в нем обозначают: DP – имя роди-тельской диаграммы, DC – имя дочерней диа-граммы, NB – название детализированного функционального блока, LP – метку дуги родительской диаграммы, NP – имя начальной вершины дуги LP на родительской диаграмме, NC – имя конечной вершины дуги LP на дочерней диаграмме.
Если соответствие между стрелками родительской и дочерней диаграмм имеется, предикат rule формирует список, состоящий из метки стрелки и ее роли на родительской диаграмме. Такой список однозначно определяет стрелку.
Если в описании дочерней диаграммы нет стрелки, соответствующей граничной стрелке родительской диаграммы, предикат rule будет иметь значение false. Такое же значение получат предикаты verify_edges, verify_node, verify_d и итоговый предикат verify.
Пример верификации функциональной модели
В качестве примера рассмотрим верификацию фрагмента обобщенной функциональной модели одностадийного химического производства. Детально построение и особенности этой модели рассмотрены в [13].
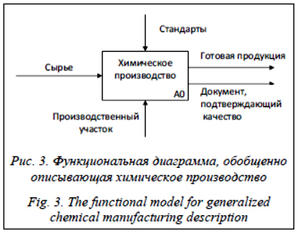 Функциональная диаграмма наивысшего уровня описывает производство как единый процесс, для которого входом является сырье, выходом – готовая продукция с документом, подтверждающим ее качество (рис. 3). В роли «управления» для этого процесса задаются стандарты (ГОСТ или ТУ), описывающие требования к качеству продукции. Исполнителем процесса, как правило, является цех или производственный участок.
Функциональная диаграмма наивысшего уровня описывает производство как единый процесс, для которого входом является сырье, выходом – готовая продукция с документом, подтверждающим ее качество (рис. 3). В роли «управления» для этого процесса задаются стандарты (ГОСТ или ТУ), описывающие требования к качеству продукции. Исполнителем процесса, как правило, является цех или производственный участок.
Представим теоретико-множественное описание графа:
A-0={N00,L00} где
N00={L, R, U, D, химическое_производство}
L00={сырье(O:L,
I:химическое_производство),
готовая_продукция(
O:химическое_производство, I:R),
документ_подтверждающий_качество(
O:химическое_производство, I:R),
стандарты(O:U,
C: химическое_производство),
производственный_участок(O:D,
M: химическое_производство)}
Поскольку в диаграмме наивысшего уровня все стрелки являются граничными, все дуги графа описывают граничные стрелки и связывают служебные вершины с единственной вершиной, которая соответствует единственному функциональному блоку диаграммы уровня А0.
 На дочерней диаграмме эта диаграмма детализирована: выделены основные технологические операции в соответствии с [14] и добавлена процедура контроля качества готовой продукции (рис. 4). Особенностями диаграммы являются обратные связи, описывающие выделение из реакционной смеси непрореагировавшего сырья, которое возвращается на этап под-готовки, и повторное разделение продукции ненадлежащего качества. Отметим также, что на этой диаграмме ветвятся две стрелки: «готовая_продукция» и «производственный_участок». Для первой из них при ветвлении дуги метки не изменяются, для второй добавляются новые метки для каждой ветви.
На дочерней диаграмме эта диаграмма детализирована: выделены основные технологические операции в соответствии с [14] и добавлена процедура контроля качества готовой продукции (рис. 4). Особенностями диаграммы являются обратные связи, описывающие выделение из реакционной смеси непрореагировавшего сырья, которое возвращается на этап под-готовки, и повторное разделение продукции ненадлежащего качества. Отметим также, что на этой диаграмме ветвятся две стрелки: «готовая_продукция» и «производственный_участок». Для первой из них при ветвлении дуги метки не изменяются, для второй добавляются новые метки для каждой ветви.
Представим теоретико-множественное описание графа:
A0={N0,L0} где
N00={L, R, U, D,
подготовка_сырья,
химическое_превращение,
разделение_смеси,
анализ_состава_продукции, N0001}
L00={сырье(O:L, I:подготовка_сырья),
подготовленное_сырье(
O:подготовка_сырья,
I:химическое_превращение),
реакционная_смесь(
O:химическое_превращение,
I:разделение_смеси),
побочные_продукты(
O:разделение_смеси, I:R),
готовая_продукция(O:разделение_смеси,
I:анализ_состава_продукции),
готовая_продукция(O:разделение_смеси,
I:R),
сырье(O:разделение_смеси,
I:подготовка_сырья),
документ_подтверждающий_качество(
O:анализ_состава_продукции, I:R),
продукция_ненадлежащего_качества(
O:анализ_состава_продукции,
I:разделение_смеси),
стандарты(O:U,
C: анализ_состава_продукции),
производственный_участок(O:D,M:N0001),
участок_подготовки_сырья (O:N0001,
M: подготовка_сырья),
реакторный_участок(O:N0001,
М: химическое_превращение),
участок_разделения(O:N0001,
М: разделение_смеси),
лаборатория_контроля_качества(O:N0001,
М: анализ_состава_продукции)}
На этом шаге отношение decompose состоит из единственной тройки, описывающей декомпозицию функционального блока «химическое_производство». Множество вершин графа включает вершины, соответствующие функциональным блокам диаграммы, вершины, задающие границы диаграммы, и вершину, задающую точку ветвления стрелки «производственный_участок» (эта вершина имеет имя N0001). Ветвление стрелки «готовая_продукция» описывают две дуги с одинаковыми метками «готовая_продукция». Описание стрелки «производственный_участок» включает в себя дугу с той же меткой, указывающую на служебную вершину, и четыре дуги, связывающие служебную вершину с вершинами, которые описывают функциональные блоки. Метки этих дуг различны («участок подготовки сырья», «реакторный участок» и т.д.).
Выполним проверку взаимосвязей этих диаграмм, используя Пролог.
База фактов, описывающих родительскую и дочернюю диаграммы, следующая:
decompose(a00,a0,manufacturing).
node(manufacturing,a00).
node(preparation,a0).
node(transformation,a0).
node(separation,a0).
node(analisys,a0).
node(n0001,a0).
edge(raw_material,o,l,i,manufacturing).
edge(standarts,o,u,c,manufacturing).
edge(product,o,manufacturing,i,r).
edge(documents,o,manufacturing,i,r).
edge(manufacturing_site,o,d, m,manufacturing).
edge(raw_material,o,l,i,preparation).
edge(prepared_material,o,preparation,i, transformation).
edge(mixture,o,transformation,i,separation).
edge(product,o,separation,i,r).
edge(co-products,o,separation,i,r).
edge(raw_material,o,separation,
i,preparation).
edge(product,o,separation,i,analisys).
edge(documents,o,analisys,i,r).
edge(defective_product,o,analisys,i, separation).
edge(standarts,o,u,c,analisys).
edge(manufacturing_site,o,d,m,n0001).
edge(preparation_site,o,n0001, m,preparation).
edge(reactor_site,o,n0001, m,transformation).
edge(separation_site,o,n0001,
m,separation).
edge(laboratory,o,n0001,m,analisys).
Первый факт – описание отношения decompose. Далее идут факты, описывающие множество вершин node. Первые пять фактов, описывающих отношение edge, задают стрелки родительской диаграммы, следующие за ними – стрелки дочерней.
 Результаты выполнения отдельных предикатов показаны на рисунке 5.
Результаты выполнения отдельных предикатов показаны на рисунке 5.
Список функциональных блоков на родительской диаграмме формируется с помощью предиката list_nodes и состоит из единственного блока manufacturing. Предикат list_edges позволяет построить список стрелок, связанных с этим блоком, предикат verify_node – проверить, что на дочерней диаграмме для каждой из этих стрелок имеется соответствующая стрелка. Таким образом, проверка модели с помощью предиката verify показывает, что модель построена правильно. Если убрать из базы фактов описание соответствующих стрелок дочерней диаграммы, например,
стандарты(O:U,C: анализ_состава_продукции),
предикат verify выдаст значение false – проверка закончится неудачей.
Заключение
Для верификации функциональных моделей разработан алгоритм построения теоре-тико-множественного описания отдельной функциональной диаграммы и предложены средства представления иерархии диаграмм, формальные правила анализа правильностипостроения взаимосвязанных диаграмм, на ос-нове которых разработан алгоритм верифика-ции функциональной модели. Реализация алго-ритма выполнена средствами логического про-граммирования на языке Пролог. Приведен пример применения разработанных алгорит-мов и программ для анализа обобщенной модели химического производства.
Литература
1. Фаулер М. Предметно-ориентированные языки программирования; [пер. с англ.]. М.: Вильямс, 2011. 576 с.
2. Федоренков В.Г., Балакшин П.В. Особенности применения предметно-ориентированных языков для тестирования веб-приложений // Программные продукты и системы. 2019. № 4. С. 601–606. DOI: 10.15827/0236-235X.128.601-606.
3. Усков А.А., Жукова А.Г. Подход к оценке сложности диаграмм SADT (IDEF0) // Программные продукты и системы. 2015. № 1. С. 34–37. DOI: 10.15827/0236-235X.109.034-037.
4. Репин В.В., Елиферов В.Г. Процессный подход к управлению. Моделирование бизнес-процессов. М.: МИФ, 2013. 544 с.
5. Вичугова А.А. Методы и средства концептуального проектирования информационных систем: сравнительный анализ структурного и объектно-ориентированного подходов // Прикладная информатика. 2014. № 1. С. 56–65.
6. Erwin Data Modeler. URL: https://erwin.com/products/erwin-data-modeler/ (дата обращения: 25.01.2021).
7. IDEF0 Diagram Software – Create IDEF0 Diagrams Rapidly with Examples and Templates. URL: https://www.edrawsoft.com/IDEF0-flowcharts.php (дата обращения: 25.01.2021).
8. Алексеев В.Е., Таланов В.А. Графы и алгоритмы. Структуры данных. Модели вычислений. М.: ИНТУИТ–БИНОМ. Лаборатория знаний, 2012. 320 c.
9. Бурляева Е.В., Бурляев В.В., Цеханович В.С. Теоретико-множественное представление функциональных моделей химических производств // Тонкие химические технологии. 2017. Т. 12. № 5. С. 71–78. DOI: 10.32362/2410-6593-2017-12-5-71-78.
10. Хабаров С.П. Интеллектуальные информационные системы. PROLOG – язык разработки интеллектуальных и экспертных систем. СПб: Изд-во СПбГЛТУ, 2013. 138 с.
11. SWI-Prologue. URL: https://www.swi-prolog.org (дата обращения: 25.01.2021).
12. Wayback Machine. ISO/IEC JTC1/SC22/WG17. URL: https://web.archive.org/web/20040811091714/http://www.sju.edu/~jhodgson/wg17/wg17web.html (дата обращения: 25.01.2021).
13. Бурляева Е.В., Разливинская С.В., Трегубов А.В. Разработка и применение обобщенной функциональной модели одностадийного химического производства // Прикладная информатика. 2016. Т. 11. № 1. С. 64–70.
14. Тимофеев В.С., Серафимов Л.А., Тимошенко А.В. Принципы технологии основного органического и нефтехимического синтеза. М.: Высшая школа, 2010. 408 с.
References
- Fowler M. Domain-Specific Languages. NJ, Upper Saddle River, Addison-Wesley Publ., 2011, 597 p. (Russ ed.: Moscow, 2011, 576 p.).
- Fedorenkov V.G., Balakshin P.V. Domain-specific languages for testing web applications. Software and Systems, 2019, no. 4, pp. 601–606. DOI: 10.15827/0236-235X.128.601-606 (in Russ.).
- Uskov A.A., Zhukova A.G. An approach to SADT (IDEF0) difficulty evaluation. Software and Systems, 2015, no. 1, pp. 34–37. DOI: 10.15827/0236-235X.109.034-037 (in Russ.).
- Repin V.V., Eliferov V.G. Process Approach to Management. Business Processes Modeling. Moscow, 2013, 544 p. (in Russ.).
- Vichugova A.A. Methods and tools for conceptual design of information systems: comparative analysis of structural and object-oriented approaches. Journal of Applied Informatics, 2014, no. 1, pp. 56–65 (in Russ.).
- Erwin Data Modeler. Available at: https://erwin.com/products/erwin-data-modeler/ (accessed January 25, 2021).
- IDEF0 Diagram Software – Create IDEF0 Diagrams Rapidly with Examples and Templates. Available at: https://www.edrawsoft.com/IDEF0-flowcharts.php (accessed January 25, 2021).
- Alekseev V.E., Talanov V.A. Graphs and Algorithms. Data Structures. Calculation Models. Moscow, 2012, 320 p. (in Russ.).
- Burlyaeva E.V., Burlyaev V.V., Tsekhanovich V.S. Set-theoretic description of functional models of chemical manufacturing. Fine Chemical Technologies, 2017, vol. 12, no. 5, pp. 71–78. DOI: 10.32362/2410-6593-2017-12-5-71-78 (in Russ.).
- Khabarov S.P. Intelligent Information Systems. PROLOG – the Language for the Development of Intelligent and Expert Systems. St.-Petersburg, 2013, 138 p. (in Russ.).
- SWI-Prologue. Available at: https://www.swi-prolog.org (accessed January 25, 2021).
- Wayback Machine. ISO/IEC JTC1/SC22/WG17. Available at: https://web.archive.org/web/
20040811091714/http://www.sju.edu/~jhodgson/wg17/wg17web.html (accessed January 25, 2021).
- Burlyaeva E.V., Razlivinskaya S.V., Tregubov A.V. Development and application of the generalized functional model of one-stage chemical manufacturing. Fine Chemical Technologies, 2016, vol. 11, no. 1,
pp. 64–70 (in Russ.).
- Timofeev V.S., Serafimov L.A., Timoshenko A.V. Principles of Technology of Basic Organic and Petrochemical Synthesis. Moscow, 2010, 408 p. (in Russ.).








