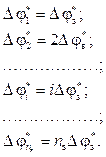Авторитетность издания
ВАК - К1
RSCI, ядро РИНЦ
Добавить в закладки
Следующий номер на сайте
№2
Ожидается:
16 Июня 2024
Программный комплекс моделирования диаграммынаправленности фазированной антенной решетки и вычисления кодов фазовращателей
Software solution for modeling of a phased antenna array radiation pattern and coding of phase shifter parameters
Дата подачи статьи: 17.10.2020
УДК: 004.942
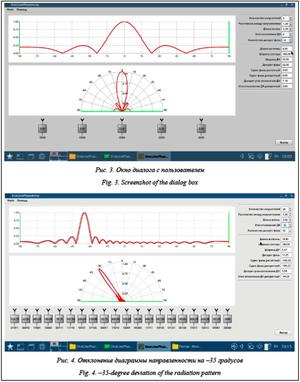
Статья опубликована в выпуске журнала № 2 за 2021 год. [ на стр. 301-306 ]Аннотация:Для обнаружения и сопровождения космических объектов необходимо управлять положением передающей и приемной диаграмм направленности в пределах сектора обзора РЛС. В современных РЛС с фазированной антенной решеткой управление положением диаграмм направленности производится фазовым методом по азимуту и углу места. Для реализации фазового метода необходимо рассчитывать фазу на каждом излучателе с фазированной антенной решеткой. В статье рассмотрены математическая модель и программная реализация процесса расчета фаз и цифровых кодов управления для каждого фазовращателя. Программный комплекс позволяет проводить исследования диаграмм направленности фазированной антенной решетки в зависимости от направления излучения, количества излучателей, дискретности фазовращателей. Программный комплекс представляет собой приложение с графическим интерфейсом, реализованное на языке программирования С++ в среде программирования Qt Creator. Анализ существующих программных комплексов моделирования диаграмм направленности фазированной антенной решетки (пакет Sensor Array Analyzer из Matlab 2013 и выше, Mathcad, CST MICROWAVE STUDIO, ANSYS HFSS) показал, что в них отсутствует возможность изменения дискретности фазовращателей, расчета кодов фазы фазовращателей и визуального представления ошибок в установке направления диаграмм направленности, зависящих от дискретности фазовращателей. Таким образом, новизна программной модели заключается в визуальном представлении теоретической диаграммы направленности и диаграммы направленности с учетом ошибок, возникащих из-за дискретности фазовращателей, что позволяет использовать ее для подготовки специалистов по фазированной антенной решетке.
Abstract:For detection and tracking of space objects, it’s necessary to control the position of transmitting and receiving radiation patterns (RP) within a section of the radar coverage area. In modern radar stations (RS) with phased antenna array (PAA), positioning of RP is performed by phase method of determining azimuth and elevation angles. For the phase method implementation, the phase of every PAA emitter must be determined. The paper presents a mathematical model and software implementation of phases and digital control code calculation for every phase shifter. The software solution allows for researching PAA RP accord-ing to the beam direction, the number of emitters, and phase shifter discreteness. The software solution is an application with a graphical interface, written in the C++ programming language in Qt Creator programming environment. Analysis of existing RP PAA simulation software systems (Sensor Array Analyzer package from Matlab 2013 and above, Mathcad, CST MICROWAVE STUDIO, ANSYS HFSS) showed that they do not have the possibility of changing the discreteness of phase shifters, calculating phase codes of phase shifters and visual representation of errors in setting the direction. Thus, the novelty of the software model lies in the visual representation of the theoretical radiation pattern and the radiation pattern, considering the errors that arise because of the discreteness of the phase shifters, which allows it to be used for training specialists in the phased array antenna.
| Авторы: Калинин Т.В. (diiimaaarik@mail.ru) - Военно-космическая академия им. А.Ф. Можайского (профессор), Санкт-Петербург, Россия, кандидат технических наук, Богомаз Д.В. (vka@mil.ru) - Военно-космическая академия им. А.Ф. Можайского (старший преподаватель), Санкт-Петербург, Россия, Хрестинин Д.В. (diiimaaarik@mail.ru) - Военно-космическая академия им. А.Ф. Можайского (преподаватель), Санкт-Петербург, Россия, Вихрев А.В. (vka@mil.ru) - Военно-космическая академия им. А.Ф. Можайского (курсант), Санкт-Петербург, Россия | |
| Ключевые слова: диаграмма направленности, фазовращатель, цифровой код, программный комплекс, среда программирования qt creator |
|
| Keywords: directivity diagram, phase shifter, digital codes, software package, qt creator programming environment |
|
| Количество просмотров: 3243 |
Статья в формате PDF |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=4819 |
Версия для печати |
| Статья опубликована в выпуске журнала № 2 за 2021 год. [ на стр. 301-306 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Программное средство для имитационного моделирования с помощью графовых моделей
- Аппаратно-программный комплекс для автоматизации контроля качества ферромагнитных материалов
- Риск-ориентированный подход к проектированию системы антитеррористической защищенности образовательных учреждений
- Программное обеспечение АСУ тренажной подготовкой операторов эрготехнических радиоэлектронных средств
- Агентный подход при моделировании динамики изменения состояния парка радиотехнических систем специального назначения
Назад, к списку статей