Программный комплекс для компьютерного моделирования процессов параметрической идентификации математических моделей конвективно-диффузионного переноса
| Кувшинова А.Н. (kuvanulspu@yandex.ru) - Ульяновский государственный педагогический университет им. И.Н. Ульянова (аспирант), Ульяновск, Россия, Цыганов А.В. (andrew.tsyganov@gmail.com) - Ульяновский государственный педагогический университет им. И.Н. Ульянова (профессор), Ульяновск, Россия, кандидат физико-математических наук | |
| Ключевые слова: matlab, оптимальное оценивание, параметрическая идентификация, дискретная линейная стохастическая модель, граничные задачи, конвективно-диффузионный перенос |
|
| Keywords: matlab, optimal estimation, parameter identification, discrete linear stochastic model, boundary problems, convection-diffusion transfer |
|
|
|
|
Для описания различных природных и технических процессов широко используются математические модели тепломассопереноса [1, 2]. Для данных моделей актуальными являются задачи идентификации их параметров по результатам измерений значений искомой функции в отдельных точках рассматриваемой области. Такого рода задачи называются обратными и в общем случае относятся к некорректно поставленным задачам математической физики [3]. Для практических приложений традиционными методами решения этих задач являются экстремальные постановки с последующей параметрической идентификацией, однако возможности применения данных методов в системах, работающих в реальном времени, существенно ограничены по причине большого объема вы- числений. В ряде работ отечественных и зарубежных авторов для решения обратных задач тепломассопереноса предлагается использовать рекуррентные методы параметрической идентификации, основанные на алгоритмах оптимальной дискретной фильтрации (преимущественно калмановского типа). Данные методы показали свою эффективность при решении задач температурной диагностики двигателей и паровых турбин [4–7], нестационарной теплометрии [8–11], конвективной диффузии [12]. В работах [13, 14] приводятся примеры применения различных модификаций фильтра Калмана и фильтра частиц к задачам теплопереноса. Применение данных методов требует проведения исследований относительно устойчивости, сходимости и оценки погрешностей получаемых результатов. В связи с этим актуальной является задача разработки ПО для проведения соответствующих исследований. Следует также заметить, что численная эффективность реализации рекуррентных методов параметрической идентификации в определенных случаях может существенно зависеть от эффективности программной реализации соответствующих методов оптимальной дискретной фильтрации. В данной работе описывается программный комплекс, предназначенный для мо- делирования процессов параметрической идентификации математических моделей конвективно-диффузионного переноса, в котором реализованы алгоритмы параметрической идентификации, предложенные в работах [15–18]. Постановка задачи Рассмотрим одномерную модель конвективно-диффузионного переноса с постоянными коэффициентами, заданную следующими уравнениями:
или
где x – пространственная координата; t – время; a и b – границы рассматриваемого отрезка; c(x, t) – искомая функция, например, концентрация загрязняющего вещества в потоке жидкости в точке с координатой x в момент времени t; v – скорость конвекции; a – коэффициент диффузии; (2) – начальное условие; (3), (4), (4¢) – граничные условия. Таким образом, рассматривается задача либо с граничными условиями первого рода, либо со смешанными граничными условиями первого и третьего рода. Задача параметрической идентификации модели (1)–(4) ((1)–(4¢)) состоит в определении коэффициентов v и α в уравнении (1), а также функций f(t) и g(t) в граничных условиях по результатам зашумленных измерений искомой функции в отдельных точках рас- сматриваемого отрезка в различные моменты времени. Дискретизация модели Для решения поставленной задачи перейдем от исходной непрерывной модели к дискретной, описываемой линейной динамической системой в пространстве состояний с зашумленными измерениями, которая в общем случае имеет следующий вид:
где ck Î ℝn – вектор состояния системы; uk Î ℝr – вектор входных воздействий; zk Î ℝm – вектор измерений; Fk Î ℝn×n, Bk Î ℝn×r, Gk Î ℝn×q, Hk Î ℝm×n – матрицы; wk Î ℝq и ξk Î ℝm – шумы, образующие независимые нормально распределенные последовательности с нулевым математическим ожиданием и ковариационными матрицами Q ≥ 0 и R > 0. Дискретизируя исходную модель в пространственно-временной области на сетке
в случае граничных условий (3) и (4) получаем дискретную линейную динамическую систему:
а в случае граничных условий (3) и (4¢):
Системы (5) и (5¢) являются детерминированными (шум wk в объекте отсутствует) дискретными линейными динамическими системами, в которых граничные условия входят в двумерный (r = 2) вектор входных воздействий uk. Коэффициенты в матрицах систем (5) и (5¢) имеют следующий вид: a1 = r1 + r2, a2 = 1 – 2r2, a3 = r2 – r1,
где В системе (5) n = N – 1 вектор состояния ck состоит из всех внутренних узлов пространственной сетки, а в системе (5¢) n = N вектор состояния ck состоит из всех внутренних узлов пространственной сетки и правой границы. Добавим к уравнениям (5) и (5¢) модель измерителя в виде уравнения зашумленных измерений:
где H Î ℝm×n – матрица измерений (структура измерителя); m – количество измеряемых компонент вектора состояния. Для решения задачи параметрической идентификации полученных дискретных моделей (5), (6) и (5¢), (6) может быть применен богатый арсенал методов оптимальной дискретной фильтрации и параметрической идентификации. Описание программного комплекса Программный комплекс реализован на языке MATLAB в виде набора скриптов и функций, позволяющих решать задачи - дискретизации модели и моделирования экспериментальных данных; - идентификации граничных условий; - идентификации коэффициентов конвекции и диффузии. Рассмотрим эти задачи подробнее. Дискретизация модели и моделирование экспериментальных данных. Для представления исходной модели используются следующие структуры: pde – коэффициенты уравнения, domain – область изменения переменных, ic – начальное условие, bc – граничные условия, bct – типы граничных условий, а для ее дискретизации: grid – пространственно-временная сетка, lds – линейная динамическая система. В структуре grid хранится информация о количестве узлов, узлах и шагах сетки, а в структуре lds – матрицы F и B. Построение сетки выполняется с помощью функции grid = compute_grid(pde, domain, nX, nT), где nX, nT – число узлов по соответствующим переменным (в случае отсутствия аргумента nT число узлов по переменной t вычисляется автоматически из условия сходимости конечно-разностной схемы). Дискретизация исходной модели выполняется при помощи функции lds = = pde2lds(pde, bc, bct, grid). Для моделирования процесса измерений используется структура sens, хранящая информацию о матрицах H и R. Измеритель задается с помощью функции sens = sensor(bct, nX, variance, problemtype), где variance – дисперсия шума в измерителе; problemtype – строковый параметр, определяющий вид матрицы H. Моделирование процесса измерений осуществляется путем последовательного решения исходного уравнения конечно-разностным методом и зашумления значений решения в выбранных точках. Для этой цели используются следующие функции: solution = solve_findiff(pde, ic, bc, bct, grid), Z = measure(solution, bct, sens), в результате чего получаются численное решение исходной задачи solution в виде матрицы размера K×N и матрица результатов измерений Z Î ℝm×K, в которой по столбцам хранятся векторы измерений zk, k = 1, 2, …, K. Рассмотрим процесс дискретизации исходной модели и моделирования процесса измерений на примере следующей задачи:
В данном случае рассматривается задача со смешанными граничными условиями вида (1), (2), (3), (4¢), где v =2, a =1, φ(x) = 0, f(t) = |sin 3πt|, g(t) = t, λ = 1. Приведем содержимое скрипта run_problem_demo с описанием модели (7)–(10): pde.v = 2; % convection speed pde.alpha = 1; % diffusion coefficient domain.a = 0; % left x bound domain.b = 1; % right x bound domain.Tmin = 0; % start time domain.Tmax = 1; % stop time
ic.f = @ic_f; % initial condition function bc.f1 = @bc_f1; % left boundary condition function bc.c1 = 1.0; % left boundary condition constant bc.f2 = @bc_f2; % right boundary condition function bc.c2 = 1.0; % right boundary condition constant
bct.t1 = 1; % left boundary condition type bct.t2 = 3; % right boundary condition type
nX = 6; % number of x-grid points variance = 0.02^2;% noise variance
grid = compute_grid(pde, domain, nX); lds = pde2lds(pde, bc, bct, grid); sens = sensor(bct, nX, variance, 'bc'); solution = solve_findiff(pde, ic, bc, bct, grid); Z = measure(solution, bct, sens);
print_grid(grid); print_lds(lds); print_sensor(sens);
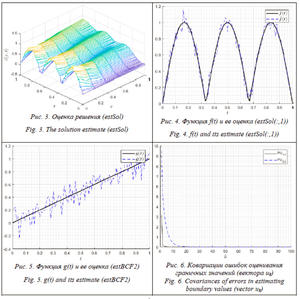
plot_conditions(ic, bc, bct, grid); plot_solution(solution, grid); plot_measurements(bct, grid, sens, Z); В скрипте выполняется дискретизация задачи на сетке с 6 пространственными узлами (количество узлов по переменной t вычисляется автоматически и равно 101), а затем моделируется процесс зашумленных измерений решения с дисперсией шумов 0.022. Для корректной работы скрипта пользователем должны быть в отдельных файлах предварительно реализованы функции ic_f, bc_f1 и bc_f2 с описанием начального и граничных условий. Например, функция, описывающая правое граничное условие, реализована в файле bc_f1.m следующим образом: function c = bc_f1(t) c = abs(sin(3*pi*t)); end В результате работы скрипта построены: – конечно-разностная сетка nX = 6 nT = 101 xGrid = 0:0.2:1 tGrid = 0:0.01:1 – линейная динамическая система F(5x5): 0.5000 0.2000 0 0 0 0.3000 0.5000 0.2000 0 0 0 0.3000 0.5000 0.2000 0 0 0 0.3000 0.5000 0.2000 0 0 0.2500 0.4167 0.1667 B(5x2): 0.3000 0 0 0 0 0 0 0 0 0.1667 – измеритель H(2x5): 1 0 0 0 0 0 0 0 0 1 R(2x2): 1.0e-03 * 0.4000 0 0 0.4000 Графики решения, полученного методом конечных разностей и смоделированных измерений, приведены на рисунках 1 и 2 соответственно. Идентификация граничных условий.
Алгоритм идентификации граничных условий реализован в виде функции [estSol, estBCF2, PHistory, PUHistory] = bc_id_gm(ic, bct, grid, lds, sens, Z). Для работы алгоритма необходимы предварительная дискретизация задачи и измерение значений решения в узлах пространственной сетки, соответствующих первому и последнему элементам вектора состояния (в случае условий первого рода это будут второй и предпоследний узлы, а в случае условий первого и третьего рода – второй и последний узлы сетки). Выходными аргументами функции являются: estSol – оценка решения в узлах пространственно-временной сетки; estBCF2 – оценка значений функции в граничном условии третьего рода; PHistory – ковариации ошибок оценивания вектора состояния; PUHistory – ковариации ошибок оценивания вектора входных воздействий. estSol представляет собой матрицу того же размера, что и матрица численного решения solution, полученного по методу конечных разностей. В случае, когда решается задача идентификации с двумя граничными условиями первого рода, их оценка сохраняется в первом и последнем столбцах estSol (вектор estBCF2 при этом является пустым), а в остальных столбцах хранятся оценки вектора состояния. Если решается задача с условиями первого и третьего рода, их оценки сохраняются соответственно в первом столбце estSol и векторе estBCF2, а в остальных столбцах хранятся оценки вектора состояния. В матрицах PHistory и PUHistory по столбцам хранятся ковариации ошибок оценивания вектора состояния и измерений соответственно, характеризующие качество получаемых оценок.
Идентификация коэффициентов конвекции и диффузии. В программном комплексе реализованы несколько методов идентификации коэффициентов уравнения (1), описанных в работах [15] и [18]. Данные методы основаны на поиске значений параметров v и α, минимизирующих критерий идентификации, который задается в виде логарифмической функции правдоподобия и строится на величинах, вычисляемых фильтром Калмана: векторе невязок измерений и на его ковариационной матрице (см., например, [20]). Для вычисления значений критерия идентификации реализованы две функции: LR = kf_lr(theta, bc, bct, grid, sens, phi, f1, f2, Z), [LR, LRG] = kf_lr_grad(theta, bc, bct, grid, sens, phi, f1, f2, Z). Первый аргумент обеих функций – вектор значений параметров θ = [v, a]. Вторая функция отличается от первой дополнительным вычислением градиента функции правдоподобия.
Минимизация критерия идентификации может выполняться различными функциями MATLAB, предназначенными для минимизации функций нескольких переменных. В программном комплексе для этих целей используются функции simulannealbnd (Simulated Annealing – метод имитации отжига), ga (Genetic Algorithm – генетический алгоритм) и fmincon (условная минимизация). Первые две функции являются безградиентными метаэвристическими методами оптимизации, и в них в качестве целевой функции используется функция kf_lr. Функция fmincon может использоваться как с градиентной (kf_lr_ grad), так и с безградиентной (kf_lr) версией функции вычисления значений критерия идентификации (во втором случае градиент целевой функции аппроксимируется самой функцией fmincon). Для идентификации коэффициентов уравнения в программном комплексе реализо- ваны функции coef_id_ga, coef_id_sa, coef_id_fmincon и coef_id_fmincon_grad с унифицированным интерфейсом. Приведем пример реализации функции coef_id_sa: function theta = coef_id_sa(ic, bc, bct, grid, sens, saOptions, LB, UB, Z, theta0) vLB = LB(1); vUB = UB(1); alphaLB = LB(2); alphaUB = UB(2);
phi = ic.f(grid.xGrid); % phi(x) f1 = bc.f1(grid.tGrid); % f(t) f2 = bc.f2(grid.tGrid); % g(t)
if nargin < 10 v0 = vLB + 0.5*(vUB-vLB); alpha0 = alphaLB + 0.5*(alphaUB-alphaLB); theta0 = [v0 alpha0]; end
objFnc = @(theta) kf_lr(theta, bc, bct, grid, sens, phi, f1, f2, Z);
[theta, fval, exitflag, output] = simulannealbnd(objFnc, theta0, [vLB alphaLB], [vUB alphaUB], saOptions);
end Описание исходной задачи, настройка параметров и вызов нужного алгоритма выполняются в скриптах run_coef_id_ga, run_coef_id_sa, run_coef_id_fmincon и run_coef_id_fmincon_grad. Представим фрагмент скрипта run_coef_id_sa и результат его выполнения (идентифицированные значения параметров v и a): ... vLB = 0; % convection speed lower bound vUB = 5; % convection speed upper bound alphaLB = 0; % diffusion coefficient lower bound alphaUB = 5; % diffusion coefficient upper bound
saOptions = saoptimset('simulannealbnd');
saOptions = saoptimset(saOptions, 'MaxIter', Inf); saOptions = saoptimset(saOptions, 'ReannealInterval', 100); saOptions = saoptimset(saOptions, 'StallIterLimit', 100); saOptions = saoptimset(saOptions, 'MaxFunEvals', Inf); saOptions = saoptimset(saOptions, 'Display', 'off'); saOptions = saoptimset(saOptions, 'DisplayInterval', 1); saOptions = saoptimset(saOptions, 'OutputFcn', @sa_out);
grid = compute_grid(pde, domain, nX); solution = solve_findiff(pde, ic, bc, bct, grid);
sens = sensor(bct, nX, variance, 'coef'); Z = measure(solution, bct, sens);
theta = coef_id_sa(ic, bc, bct, grid, sens, saOptions, [vLB alphaLB], [vUB alphaUB], Z);
disp(['v = ', num2str(theta(1),15), ', alpha = ', num2str(theta(2),15)]); ... >> run_coef_id_sa v = 1.94311777853335, alpha = 0.989708385847537 Заключение В статье описан программный комплекс, предназначенный для моделирования процессов параметрической идентификации одномерных моделей конвективно-диффузионного переноса с постоянными коэффициентами, в котором реализованы методы параметрической идентификации коэффициентов и граничных условий математической модели. Помимо основных функций параметрической идентификации и различных вспомога- тельных функций, в программном комплексе реализованы скрипты, упрощающие решение задач параметрической идентификации, а также используемые для проведения серий экспериментов по исследованию статистических свойств реализованных алгоритмов (например, точности и времени идентификации). Данный программный комплекс может служить удобным средством для разработки и исследования новых алгоритмов параметрической идентификации и оптимального оценивания моделей конвективно-диффузионного переноса на основе алгоритмов оптимальной дискретной фильтрации. В настоящее время авторами ведется работа по созданию и реализации новых алгоритмов параметрической идентификации. Литература 1. Леонтьев А.И. Теория тепломассообмена. М.: Изд-во МГТУ, 1997. 683 с. 2. Фарлоу С. Уравнения с частными производными для научных работников и инженеров; [пер. с англ.]. М.: Мир, 1985. 384 с. 3. Денисов А.М. Введение в теорию обратных задач. М.: Изд-во МГУ, 1994. 208 с. 4. Симбирский Д.Ф. Температурная диагностика двигателей. Киев: Техника, 1976. 208 с. 5. Мацевитый Ю.М., Мултановский А.В. Идентификация параметров теплообмена методом оптимальной динамической фильтрации // ТВТ. 1979. Т. 17. № 5. С. 1053–1060. 6. Карпов А.А., Тихонова Т.А. Восстановление нестационарных тепловых потоков по экспериментальным данным // Матем. моделирование. 2000. Т. 12. № 5. С. 101–106. 7. Симбирский Г.Д., Лантрат В.К. Применение цифрового фильтра Калмана для параметрической идентификации высокотемпературного термопреобразователя // Автомобиль и электроника. Современные технологии. 2017. № 11. С. 68–75. 8. Пилипенко Н.В. Применение фильтра Калмана в нестационарной теплометрии. СПб: Изд-во Университет ИТМО, 2017. 36 с. 9. Пилипенко Н.В., Заричняк Ю.П., Иванов В.А., Халявин А.М. Параметрическая идентификация дифференциально-разностных моделей теплопереноса в одномерных телах на основе алгоритмов фильтра Калмана // Научно-технический вестник информационных технологий, механики и оптики. 2020. Т. 20. № 4. С. 584–588. DOI: 10.17586/2226-1494-2020-20-4-584-588. 10. Daouas N., Radhouani M.-S. A new approach of the Kalman filter using future temperature measurements for nonlinear inverse heat conduction problems. Numerical Heat Transfer Fundamentals, 2004, vol. 45, no. 6, pp. 565–585. DOI: 10.1080/10407790490430598. 11. Pacheco C.C., Orlande H.R.B., Colaço M.J., Dulikravich G.S. Identification of a position and time dependent heat flux by using the Kalman filter and improved lumped analysis in heat conduction. Proc. ICCM2014, 2014, Cambridge, England, pp. 801–809. 12. Матвеев М.Г., Копытин А.В., Сирота Е.А. Комбинированный метод идентификации параметров распределенной динамической модели // Сб. тр. IV Междунар. конф. ИТНТ. 2018. С. 1651–1657. 13. Myers M.R., Jorge A.B., Mutton M.J., Walker D.G. A comparison of extended Kalman filter, ultrasound time-of-flight measurement models for heating source localization. Inverse Problems in Science and Engineering, 2012, vol. 20, no. 7, pp. 991–1016. DOI: 10.1080/17415977.2012.669272. 14. Orlande H.R.B., Colaço M.J., Dulikravich G.S., Vianna F.L.V. et al. State estimation problems in heat transfer. Int. J. for Uncertainty Quantification, 2012, vol. 2, no. 3, pp. 239–258. DOI: 10.1615/Int.J. UncertaintyQuantification.2012003582. 15. Tsyganov A.V., Tsyganova Yu.V., Kuvshinova A.N., Tapia Garza H.R. Metaheuristic algorithms for identification of the convection velocity in the convection-diffusion transport model. Proc. II Int. Sci. and Pract. Conf. FTI, 2018, pp. 188–196. 16. Цыганов А.В., Цыганова Ю.В., Кувшинова А.Н. Динамическая идентификация граничных условий в модели конвективно-диффузионного переноса в условиях зашумленных измерений // Сб. тр. V Междунар. конф. ИТНТ. 2019. Т. 3. С. 169–177. 17. Кувшинова А.Н. Динамическая идентификация смешанных граничных условий в модели конвективно-диффузионного переноса в условиях зашумленных измерений // Журнал Средневолжского математического общества. 2019. Т. 21. № 4. С. 469–479. DOI: 10.15507/2079-6900.21.201904. 469-479. 18. Кувшинова А.Н., Цыганов А.В., Цыганова Ю.В., Тапиа Гарса У.Р. Алгоритм численной идентификации параметров в модели конвективно-диффузионного переноса // Сб. тр. VI Междунар. конф. ИТНТ. 2020. С. 825–832. 19. Gillijns S., Moor B.D. Unbiased minimum-variance input and state estimation for linear discrete-time systems. Automatica, 2007, vol. 43, no. 1, pp. 111–116. DOI: 10.1016/j.automatica.2006.08.002. 20. Astrom K.J. Maximum likelihood and prediction error methods. Automatica, 1980, vol. 16, no. 5, pp. 551–574 References 1. Leontyev A.I. Theory of Heat and Mass Transfer. Moscow, 1997, 683 p. (in Russ.). 2. Farlow S.J. Partial Differential Equations for Scientists and Engineers. John Wiley and Sons Publ., 1982, 429 p. (Russ. ed.: Moscow, 1985, 384 p.). 3. Denisov A.M. Introduction to the Theory of Inverse Problems. Moscow, 1994, 208 p. (in Russ.). 4. Simbirskiy D.F. Temperature Diagnostics of Engines. Kiev: Tekhnika, 1976, 208 p. (in Russ.). 5. Matsevity Yu.M., Multanovsky A.V. Identification of heat transfer parameters using the optimal dynamic filtration method. High Temperature, 1979, vol. 17, no. 5, pp. 1053–1060 (in Russ.). 6. Karpov A.A., Tikhonova T.A. Recovery of non-stationary heat flows from experimental data. Matem. Mod., 2000, vol. 12, no. 5, pp. 101–106 (in Russ.). 7. Simbirsky G.D., Lantrat V.K. Application of the Kalman digital filter for parametric identification high-temperature thermocouple. Avtomobil i Elektronika. Sovremennye Tekhnologii, 2017, no. 11, pp. 68–75 (in Russ.). 8. Pilipenko N.V. Applying the Kalman Filter in Non-Stationary Heat Metering. St. Petersburg, 2017, 36 p. (in Russ.). 9. Pilipenko N.V., Zarichnyak Yu.P., Ivanov V.A., Halyavin A.M. parametric identification of differencial-difference models of heat transfer in on e-dimensional bodies based on Kalman filter algorithms. Sci. Tech. J. Inf. Technol. Mech. Opt., 2020, vol. 20, no. 4, pp. 584–588 (in Russ.). DOI: 10.17586/2226-1494-2020-20-4-584-588 . 10. Daouas N., Radhouani M.-S. A new approach of the Kalman filter using future temperature measurements for nonlinear inverse heat conduction problems. Numerical Heat Transfer Fundamentals, 2004, vol. 45, no. 6, pp. 565–585. DOI: 10.1080/10407790490430598 . 11. Pacheco C.C., Orlande H.R.B., Colaço M.J., Dulikravich G.S. Identification of a position and time dependent heat flux by using the Kalman filter and improved lumped analysis in heat conduction. Proc. ICCM2014, 2014, Cambridge, England, pp. 801–809. 12. Matveev M.G., Kopytin A.V., Sirota E.A. Combined method for identifying the parameters of a distributed dynamic model. Proc. IV Int. Conf. ITNT, 2018, pp. 1651–1657 (in Russ.). 13. Myers M.R., Jorge A.B., Mutton M.J., Walker D.G. A comparison of extended Kalman filter, ultrasound time-of-flight measurement models for heating source localization. Inverse Problems in Science and Engineering, 2012, vol. 20, no. 7, pp. 991–1016. DOI: 10.1080/17415977.2012.669272 . 14. Orlande H.R.B., Colaço M.J., Dulikravich G.S., Vianna F.L.V. et al. State estimation problems in heat transfer. Int. J. for Uncertainty Quantification, 2012, vol. 2, no. 3, pp. 239–258. DOI: 10.1615/Int.J.UncertaintyQuantification.2012003582 . 15. Tsyganov A.V., Tsyganova Yu.V., Kuvshinova A.N., Tapia Garza H.R. Metaheuristic algorithms for identification of the convection velocity in the convection-diffusion transport model. Proc. II Int. Sci. and Pract. Conf. FTI, 2018, pp. 188–196. 16. Tsyganov A.V., Tsyganova Yu.V., Kuvshinova A.N. Dynamic identification of boundary conditions for convection-diffusion transport model in the case of noisy measurements. Proc. V Int. Conf. ITNT, 2019, vol. 3, pp. 169–177 (in Russ.). 17. Kuvshinova A.N. Dynamic identification of mixed boundary conditions for convection-diffusion transport model in the case of noisy measurements. Middle Volga Mathematical Society J., 2019, vol. 21, no. 4, pp. 469–479 (in Russ.). DOI: 10.15507/2079-6900.21.201904.469-479 . 18. Kuvshinova A.N., Tsyganov A.V., Tsyganova Yu.V., Tapia Garza H.R. Algorithm for numerical identification of parameters for convective-diffusion transport model. Proc. VI Int. Conf. ITNT, 2020, pp. 825–832 (in Russ.). 19. Gillijns S., Moor B.D. Unbiased minimum-variance input and state estimation for linear discrete-time systems. Automatica, 2007, vol. 43, pp. 111–116. DOI: 10.1016/j.automatica.2006.08.002 . 20. Astrom K.J. Maximum likelihood and prediction error methods. Automatica, 1980, vol. 16, no. 5, |
http://swsys.ru/index.php?page=article&id=4858&lang=&lang=%E2%8C%A9=en&like=1 |
|
Perhaps, you might be interested in the following articles of similar topics:
- Автоматизированное проектирование инструментов на основе моделирования технологии выдавливания металлов
- Программные средства вейвлет-фрактально-корреляционного метода обнаружения объектов космического мусора
- Применение искусственных нейронных сетей в системах автоматического управления магнитной левитацией
- Показатели безопасности космического аппарата в полете и генерация информации для предупреждения о высокоскоростном взаимодействии
- Разработка генератора паролей с использованием GUI MATLAB


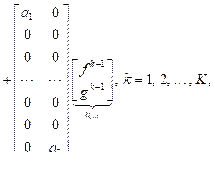 (5)
(5)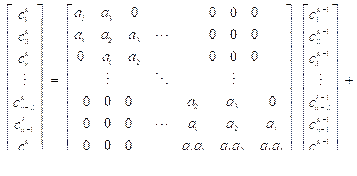
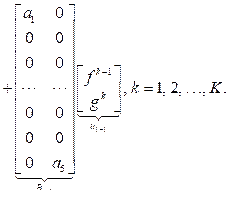 (5¢)
(5¢) (6)
(6)