Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Метод создания параллельных программных средств моделирующих комплексов военного назначения
Аннотация:В статье рассмотрены вопросы выбора алгоритмов распараллеливания, реализованных в инструментальных средствах разработки параллельных программ для многоядерных (многопроцессорных) вычислительных систем с общей памятью. Целью данного исследования является оценка влияния времени выполнения распараллеленных циклических участков целевой программы при многопоточном параллельном выполнении программы в многоядерных (многопроцессорных) ПЭВМ на показатели результатов имитационного моделирования боевых действий. Научная новизна заключается в разработке нового метода создания параллельных программных средств моделирующих комплексов военного назначения. Проведенный анализ современных программных средств моделирующих комплексов военного назначения показал, что на оперативность их применения при использовании по назначению в значительной степени оказывает влияние продолжительность расчетов при проведении моделирования. В работе приведены примеры расчетов в среде Mathcad. Для исключения ошибок выбора предпочтительных алгоритмов распараллеливания анализ производился на основе элементов математической статистики с введением вероятности доверительного интервала для оценки времени выполнения цикла определенным алгоритмом по верхней границе доверительного интервала. Предложен вариант построения программных средств на примере внедрения технологических разработок в программную архитектуру моделирующего комплекса.
Abstract:Nowadays modeling systems are actively created and used all over the world including the Armed Forces of the Russian Federation. The basis of these systems are modeling complexes, which are a set of technical and software tools providing calculations and imitation modeling. The analysis of modern software tools for modeling military complexes has shown that the duration of the cal-culations performed during imitation largely influence the efficiency of their application when used directly. Specific technological tools used in the development of parallelization of labor-intensive cyclic sections of modeling complexes allow minimizing the time spent on modeling under conditions of limited terms of using software tools. However, nowadays they are not implemented in the general software architecture of modeling complexes accepted for supply in the Armed Forces of the Russian Federation. The paper considers the issues of choosing parallelization algorithms implemented in parallel software devel-opment tools for multi-core (multiprocessor) shared memory computing systems. The purpose of the paper is to assess the impact of the execution time of parallelized cyclic sections of a target program with multithreaded parallel execution of the program in multi-core (multiprocessor) PCs on the results of combat imitation. The scientific novelty is in the development of a new method for creating parallel software tools for modeling military complexes. The paper provides numeric examples of calculations in the Mathcad. To avoid errors in choosing preferred parallelization algorithms, the entire analysis is based on mathematical statistics elements with the probability of a confidence interval for estimating the cycle execution time by a certain algorithm considering the upper limit of the confidence interval. The author proposes a variant of constructing software tools on the example of introduc-ing technological developments into a software architecture of a modeling complex.
| Авторы: Аксенов М.А. (aksen1985@mail.ru) - Военная академия воздушно-космической обороны им. Г.К. Жукова (адъюнкт), Тверь, Россия | |
| Ключевые слова: программное средство, моделирующий комплекс, алгоритм распараллеливания, цикл, число итераций, время выполнения |
|
| Keywords: software, modeling complex, parallelization algorithm, cycle, number of iterations, execution time |
|
| Количество просмотров: 2310 |
Статья в формате PDF |
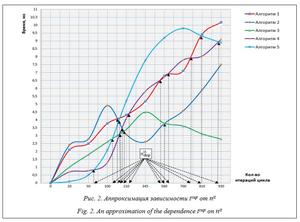
Результаты анализа применения программных средств моделирующих комплексов военного назначения (ПС МК ВН) на мероприятиях оперативной подготовки показали, что наряду с их достоинствами имеются и существенные недостатки. Основным из них является значительное превышение нормативных сроков представления результатов имитационного моделирования (выходных параметров) в условиях ограничений по времени применения ПС МК ВН в соответствии с их назначением, что не согласуется с временным алгоритмом работы должностных лиц ВС РФ [1]. В современных архитектурах ПЭВМ, поддерживающих параллелизм в многоядерных (многопроцессорных) вычислительных системах с общей памятью, наиболее распространены универсальные средства программирования: стандарты и технологии, предназначенные для создания современных параллельных программ, такие как языковые средства за- дания параллельности в программе, автома- тические средства поиска параллельных вычислений и последующего представления их с использованием существующих библиотек поддержки параллельности [2]. Для распарал- леливания целесообразно рассматривать циклические участки программы, так как около 80 % возможностей для распараллеливания заключено именно в циклах [3]. В современной технической литературе существуют работы, описывающие методы сравнения средств распараллеливания, которые применяют различные метрики. Однако они имеют общий недостаток: сравнение технологий осуществляется либо на подготовленных тестах, либо теоретически, а в некоторых из них рассматриваются только время обучения и трудоемкость реализации процесса [4–6 и др.]. Имеется тенденция к объединению нескольких средств распараллеливания в одной разрабатываемой программе. Сопоставительный анализ разработанных ранее методов применения средств параллельного программирования показывает, что они не учитывают следующее: - случайный характер изменений параметров в структуре одних и тех же циклов программы по количеству итераций цикла и времени выполнения, что приводит к изменению критических по времени выполнения циклов и может стать причиной ошибочного выбора предпочтительного алгоритма распараллеливания; - зависимость эффективности использования различных средств параллельного программирования от числа итераций цикла и от его внутренней структуры; - разная зависимость временных затрат на выполнение одного того же участка програм- много кода для разных средств распараллеливания при одних и тех же требованиях к аппаратно-программному обеспечению. Идея предлагаемого в данном исследовании метода состоит в создании системы параллельного программирования. Программист на традиционных языках программирования (С, С ++) создает программу с параллельными вычислениями. В случае возникновения проблем с анализом он может добавить подсказки в программу, разрешив какой-либо конфликт, мешающий определению параллельности. Затем найденные параллельные вычисления автоматически представляются в параллельных терминах конкретной архитектуры. По сути, это некоторая интерактивная среда разработки параллельных программ, в которой сбалансированы усилия человека и автоматических средств. В предложенном подходе основную роль при анализе, модернизации и инструментировании параллельного кода выполняет средство распараллеливания, а разработчик (программист) прагмами разрешает конфликты (если они возникают), с которыми статический анализатор может не справиться. Разработанный метод реализует автоматический выбор предпочтительного алгоритма распараллеливания из доступного набора алгоритмов под каждый конкретный циклический участок текущей программы по минимальному времени выполнения цикла. Для этого используются накопленные при тестировании статистические данные в виде массива временных профилей программы и составленного на их основе профиля проекта, представляющего собой совокупность кортежей предпочтительных алгоритмов распараллеливания, функционально связанных с текущим числом итераций цикла. В предлагаемом методе по входным параметрам из выполняемой программы ПС МК ВН (номеру цикла и количеству итераций данного цикла) с использованием составленного кортежа предпочтительных алгоритмов распараллеливания в реальном масштабе времени определяется номер алгоритма распараллеливания. Целью данной статьи является оценка влия- ния процесса автоматизации выбора предпочтительного алгоритма распараллеливания из доступного набора алгоритмов под каждый циклический участок целевой программы при многопоточном параллельном выполнении программы в многоядерных (многопроцессорных) ПЭВМ на показатели результатов имитационного моделирования боевых действий.
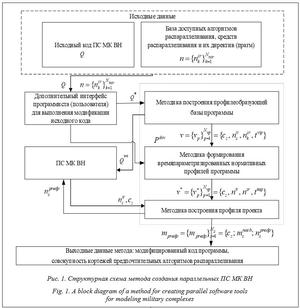
Методика построения профилеобразующей базы программы Для реализации методики необходимо выполнить определенную последовательность действий. В исходном коде ПС МК ВН выявляются циклы, имеющие счетчик числа итераций (циклы со счетчиком) и не имеющие в теле цикла команд принудительного выхода из него. Для разбора конструкции цикла проводится синтаксический анализ исходного кода программы, в ходе которого символы этого кода группируются в лексемы (распознанные группы символов) в соответствии с набором токенов, а затем в конструкции цикла в соответствии с деревом разбора. Изначально в исходном коде программы выделяются лексемы: параметр цикла, тело цикла. Выявление цикла выполняется по последовательности символов, содержащихся в токенах. В сформированных лексемах в ходе лексического анализа идентифицируются входящие в них токены, определяются параметры токенов. В ходе разбора конструкции цикла выявляются по вхождению в состав лексемы: вложенные циклы, тело цикла, параметры цикла. Циклы номеруются, клонируются, в клоны добавляются прагмы алгоритмов распараллеливания. Полученный код программы компилируется, и производится многократный запуск на тестовый прогон для получения первых статистических данных по всем циклическим участкам с примененными алгоритмами распараллеливания и вариантами числа итераций. В результате тестовых запусков формируется профилеобразующая база программы, состоящая из набора кортежей таблицы: В таблице 1 приведен пример профилеобразующей базы первичной статистики, который формируется в результате многократного тестового прогона цикла с возможностью распараллеливания пятью алгоритмами при 20 дискретных итерациях. Данный профиль программы первичной статистики представляет собой массив статистических данных, состоящих из записей четырех параметров: номер цикла cz, количество итераций цикла Методика формирования времяпараметризированных нормативных профилей Поскольку функция распределения вероятности времени выполнения цикла неизвест- на [7], из полученной профилеобразующей базы программы формируются эмпирические функции распределения времени выполнения каждого цикла следующим образом: - формируется выборка из профилеобразующей базы первичной статистики для одного значения: номера цикла cz, числа итераций - элементы массива времен выполнения цикла - рассчитываются j-е значения функции распределения для ранжированного массива Таблица 1 Пример профилеобразующей базы первичной статистики с алгоритмами распараллеливания Table 1 An example of a profile forming base of primary statistics with parallelization algorithms
Примечание: номер цикла cz = 1, количество итераций цикла Эмпирическая функция распределения аппроксимируется гладкой кривой. Так как вид функции распределения неизвестен, необходимо применять непараметрические методы аппроксимации. В [8] показано, что высокая точность аппроксимации непараметрическим методом как унимодальных, так и полимодальных распределений, заданных на конечных интервалах, обеспечивается применением полиномов Бернштейна. При этом оценка функции распределения описывается выражением
где Nb – степень полинома Бернштейна; wn – весовые коэффициенты полинома Бернштейна; Расчет параметров оценочной функции Для принятия решения и оценки погрешности по возможности использования аппроксимирующей функции рассчитывается доверительный интервал для каждого j-го значения эмпирической функции распределения:
где x – квантиль нормального распределения для заданной доверительной вероятности (например, для Pdov = 0.99, значение x = 2.576). Аппроксимирующая функция принимается при выполнении для всех j-х значений эмпирической функции распределения условия В противном случае степень полинома Nb увеличивается на единицу и выполняется повторный расчет весовых коэффициентов. Расчет значения верхней границы tsup времени выполнения цикла осуществляется путем решения уравнения P*(tsup) = Pdov. Ввиду того, что отсутствуют аналитические способы решения данного уравнения, поиск tsup выполняется численным методом. При этом появляется возможность сравнить по данному детерминированному параметру разные средства распараллеливания цикла и произвести выбор с минимальным временем. Далее с использованием рассчитанного значения tsup формируется времяпараметризированный нормативный профиль программы: В таблице 2 представлен времяпараметризированный нормативный профиль с расчетным временем (по верхней границе доверительного интервала) выполнения цикла, кото- рый получен в результате переработки профилеобразующей базы первичной статистики таблицы 1 по методике формирования времяпараметризированных нормативных профилей. Таблица 2 Пример обработанного времяпараметризированного нормативного профиля программы Table 2 An example of a processed time parameterized standard program profile
Примечание: номер цикла cz = 1, количество итераций цикла Представим результаты расчетов в Mathcad 15.0 математического аппарата методики формирования времяпараметризированных нормативных профилей, заключающейся в построении эмпирической функции распределения случайной величины времени выполнения одного заданного цикла заданным средством распараллеливания при заданном числе итераций цикла (20) и пятикратном запуске. В приведенном примере значение верхней границы времени выполнения цикла tsup заданным средством составляет 2.096 сек. Для выбора алгоритма с минимальным временем в данном примере необходимо аналогично строить эмпирические функции распределения для всех номеров алгоритмов распараллеливания с определением времени верхней границы заданного доверительного интервала. Рассмотрим следующие исходные данные: – вектор времени выполнения цикла:
– доверительная вероятность: Решение: 1. Сортировка вектора времен по возрастанию: Размерность исходного вектора времен вы- полнения цикла:
2. Формирование вектора времени выполнения цикла без повторяющихся значений времени:
Размерность преобразованного вектора времен выполнения цикла:
3. Формирование эмпирической функции распределения:
4. Упрощенный расчет верхней границы времени:
Методика построения профиля проекта Для исследуемого порядкового номера цикла c времяпараметризированный нормативный профиль перерабатывается и представляется в виде матрицы
где Массив ранжирован по возрастанию значений Интерполяция и экстраполяция времяпараметризированного нормативного профиля про- граммы При использовании кубических сплайнов на каждом из отрезков
где nit – текущее число итераций цикла; Рассчитанные значения коэффициентов сплайна сохраняются в оперативной памяти для их дальнейшего использования.
Поскольку предпочтительный алгоритм выбирается в процессе штатной работы программы, необходимо минимизировать время выбора. Для этого времяпараметризированный нормативный профиль программы Для этого организуется цикл по числу итераций Так как в точках пересечения сплайнов значения аппроксимирующих функций fq1,s(nit), fq2,s(nit) имеют одинаковую величину, они приравниваются друг к другу. В результате выполняется поиск действительных корней кубического уравнения относительно переменной nit (абсцисс точек пересечения):
Далее анализируется попадание найденных корней nit в рассматриваемый интервал
Для каждого интервала
В результате после объединения смежных интервалов с одинаковыми предпочтительными алгоритмами распараллеливания формируется профиль проекта с числом элементов Пример профиля проекта представлен в таблице 3. Он получен в результате обработки времяпараметризированного нормативного профиля таблицы 2 с расчетным временем (по верхней границе доверительного интервала) выполнения цикла по методике построения профиля проекта. В таблице 3 отражен конечный профиль проекта для указанного диапазона итераций цикла. Он представляет собой совокупность кортежей, состоящих из трех параметров: номер цикла cz, начальное количество итераций цикла Таблица 3 Пример профиля проекта Table 3 An example of a project profile
Приведем пример расчетов в Mathcad 15.0 по методике построения профиля проекта, представляющий собой совокупность кортежей предпочтительных алгоритмов распараллеливания. В нем значительно расширены значения параметра количества итераций до десяти дискретных точек, первая из которых с временем tsup = 2.096 сек., при количестве итераций 20 (табл. 1–3).
Решение. 1. Число алгоритмов распараллеливания: 2. Число итераций цикла 3. Вектор дополнительного числа итераций:
Целая часть: Число дополнительных итераций:
4. Матрица дополнительных элементов:
5. Расширенный профиль: объединение матриц по горизонтали 6. Отсортированный профиль (по возрастанию числа итераций):
Количество итераций в расширенном профиле 7. Начальный профиль проекта предпочтительных алгоритмов распараллеливания:
Количество строк начальной матрицы:
8. Конечный профиль предпочтительных алгоритмов распараллеливания:
Количество строк:
9. Выбор предпочтительного алгоритма распараллеливания:
Входной параметр – число итераций цикла
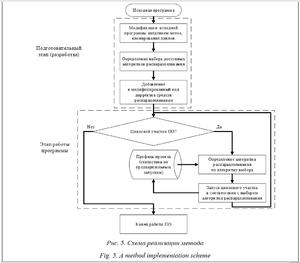
В ходе штатного выполнения программы определяется текущее число итераций цикла Опишем разработанную программу, реализующую предлагаемый метод [9]. Структура макета программы содержит перечень соответствующих программных модулей, представленных на рисунке 3.
Таблицы БД связаны с программной реализацией и исполняемым кодом ПС МК ВН. Таблица «Алгоритмы распараллеливания» заполняется до начала разработки средствами используемой СУБД. Таблица «Профилеобразующая база программы» заполняется в процессе проведения тестовых запусков разрабатываемого ПС с использованием добавленной в ПС соответствующей библиотеки, реализующей заявленный метод. Таблицы «Нормативный времяпараметризированный профиль» и «Профиль проекта» рассчитываются и заполняются после окончания выполнения тестовых запусков разрабатываемой программы. Таблица «Профиль проекта» дополнительно обновляется в процессе работы готового ПС МК ВН. На рисунке 5 представлена схема програм- мной реализации предлагаемого метода. Тело программного кода увеличивается на определенное количество клонов циклов, равное количеству алгоритмов распараллеливания, реализованных средствами распараллеливания, но при этом продолжительность исполнения программы остается прежней, так как выполняется только один выбранный клон. Процесс управления и выбор клона (с примененным алгоритмом распараллеливания) позволяет снизить временные затраты на выполнение циклических участков программы и в целом всей программы. Это связано с тем, что временные затраты на выполнение одного и того же циклического участка с заданным количеством итераций при применении разных средств рас- параллеливания будут существенно отли- чаться. Поэтому оптимизация выбора ветки (клона) программы позволяет снизить временные затраты на выполнение цикла и программы в целом. Работа автоматизирована, по входным параметрам циклического участка целевой программы (номера цикла и количества итераций в цикле) происходит выбор предпочтительного алгоритма распараллеливания.
Апробация предлагаемого метода и имитационные эксперименты были проведены на базе Военной академии воздушно-космиче- ской обороны (г. Тверь) с использованием многофункционального МК ВН «Небосвод 2.0», позволяющего моделировать боевые действия противоборствующих группировок в воздушно-космической сфере и оценивать их результаты в едином интерактивном пространственно-временном контуре управления. Программные средства комплекса разработаны в программно-технической среде Microsoft Visual Studio 2015 (язык программирования С++, СУБД PostgreSQL) [11]. В качестве варианта построения програм- мных средств МК ВН можно привести пример внедрения технологических решений в универсальную программную архитектуру имитационно-моделирующей системы «ИМС 2.0» (см. http://www.swsys.ru/uploaded/image/2022-1/ 2022-1-dop/8.jpg) [12]. Это позволит организовать дальнейшие разработки (модернизацию) перспективных программных средств на единой методической и технологической основе с учетом их использования по назначению. Заключение Таким образом, представленный метод создания параллельных ПС МК ВН дает возможность комбинировать алгоритмы распараллеливания и при необходимости комплексно применять их для каждого распараллеливаемого цикла, что позволяет сократить время выполнения ПС МК ВН, то есть время имитационного моделирования отражения удара противника с использованием программных средств моделирования автоматизированных систем военного назначения. Научная новизна заключается в том, что разработанный метод за счет выбора предпочтительного алгоритма распараллеливания под каждый циклический участок программы с учетом времени их выполнения позволит ми- нимизировать время выполнения ПС МК ВН, сократив таким образом время моделирования. В предлагаемом методе установлена функциональная связь между количеством итераций текущего цикла и предпочтительным алгоритмом распараллеливания. Автоматический выбор предпочтительного алгоритма распараллеливания производится на основе классификационного отбора по входному параметру (количеству итераций) цикла в сформированном профиле проекта, состоящем из совокупности кортежей предпочтительных алгоритмов распараллеливания. Метод может быть использован при разработке ПС МК ВН, применяемых при моделировании боевых действий в воздушно-космической сфере. Литература 1. Лясковский В.Л., Ризаев Р.Н., Допира Р.В., Кучеров Ю.С. Методика оценки степени влияния модели системы управления на эффективность применения частей и подразделений радиоэлектронной борьбы в моделирующих комплексах военного назначения // Вопросы радиоэлектроники. 2020. № 10. С. 46–52. DOI: 10.21778/2218-5453-2020-10-46-52. 2. Волконский В.Ю., Брегер А.В., Бучнев А.Ю., Грабежной А.В. и др. Методы распараллеливания программ в оптимизирующем компиляторе // МЦСТ. URL: http://www.mcst.ru/metody-rasparallelivaniya-programm-v-optimiziruyushhem-kompilyatore (дата обращения: 10.07.2021). 3. Биллиг В.А. Параллельные вычисления и многопоточное программирование. М.: ИНТУИТ, 2016. 310 с. 4. Самхарадзе К.К., Ерошенко Я.Б. Сравнительный анализ эффективности применения технологий параллельного программирования // Научный аспект. 2018. Т. 2. № 2. С. 223–236. 5. Керп А.С. Сравнение технологий распараллеливания вычислений на примере решения задачи о кручении стержня прямоугольного сечения // XVIII Всерос. конф. молодых ученых по матем. моделированию и информационным технологиям. 2017. С. 8–9. 6. Ханкин К.М. Сравнение эффективности технологий OpenMP, nVidia CUDA и StarPU на примере умножения матриц // Вестн. Южно-Уральского гос. ун-та. 2013. № 1. С. 34–41. 7. Вентцель Е.С. Теория вероятностей. М.: Юстиция, 2018. 658 с. 8. Голик Ф.В. Аппроксимация эмпирических распределений вероятностей полиномами Бернштейна // Журнал радиоэлектроники. 2018. № 7. URL: http://jre.cplire.ru/jre/jul18/5/text.pdf (дата обращения: 10.08.2021). DOI: 10.30898/1684-1719.2018.7.5. 9. Шлее М. Qt 5.10. Профессиональное программирование на С++. СПб: БХВ-Петербург, 2018. 1072 c. 10. Моргунов Е.П. PostgreSQL. Основы языка SQL. СПб: БХВ-Петербург, 2018. 336 с. 11. Гончаров А., Костров С, Бегларян С. Чем обусловлено создание нового тренажно-моделирующего комплекса // ВКС. 2017. № 4. С. 64–70. 12. Ляпин В.Р., Барвиненко В.В. Единая информационно-моделирующая среда в системах военного назначения // Военная мысль. 2015. № 4. С. 72–78. References
|
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=4879&lang= |
Версия для печати |
| Статья опубликована в выпуске журнала № 1 за 2022 год. [ на стр. 083-094 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Расширяемая система генерации заданий
- Метод построения программных средств моделирующих комплексов военного назначения
- О реализации средств машинного обучения в интеллектуальных системах реального времени
- Реализация методов обучения с подкреплением на основе темпоральных различий и мультиагентного подхода для интеллектуальных систем реального времени
- Комплекс программных средств для анализа причинно-следственных факторов конфликта применения тренажеров эрготехнических радиоэлектронных средств
Назад, к списку статей



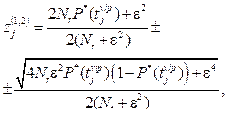
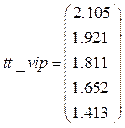 ;
;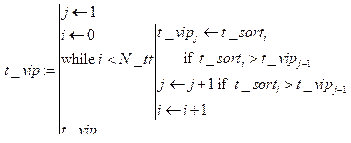
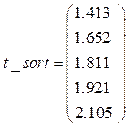 .
.
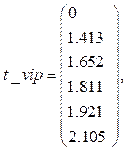
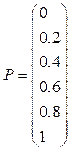 .
.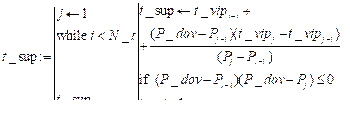
 ,
,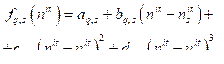
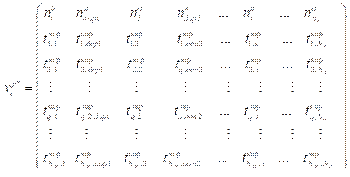
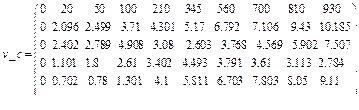
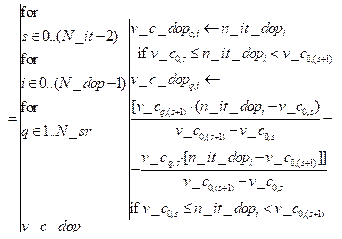

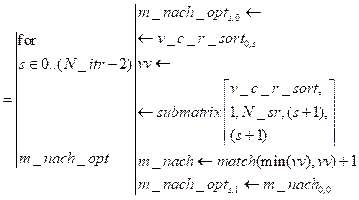
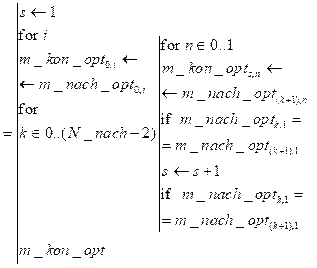
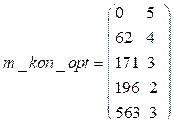 .
.