Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Информационная система оптимизации расписания доставки грузов от производителей сырья
Аннотация:
Abstract:
| Авторы: Максимов А.А. () - , Козлов А.С. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 16474 |
Версия для печати Выпуск в формате PDF (1.18Мб) |
Жесткие финансовые условия, в которых осуществляется планирование поставок продукции, низкий уровень надежности предприятий-поставщиков, большие временные интервалы между началом планирования поставок и их реальным осуществлением обостряют вопросы сырьевого обеспечения предприятий-грузополучателей. Актуальность проблемы заставляет искать новые методы, подходы организации обеспечения предприятия-потребителя с позиции своевременности обеспечения и одновременно минимизации сопутствующих расходов. Необходимость полного, своевременного обеспечения предприятия-грузополучателя продукцией при минимальных затратах и выделяемых ресурсах составляет противоречие. Для его разрешения используется логистический подход к процессу доставки грузов. Частной задачей этого подхода является проблема оптимизации расписания поставок грузов на предприятие. Указанная задача на основе разработки математической модели и ее последующей реализации в виде специализированной информационной системы решена для Челябинского электрометаллургического комбината (ЧЭМК). Актуальность проблемы для этого комбината во многом определяется тем, что анализ статистических данных по перевозке грузов на ЧЭМК указывает на многократное увеличение транспортных издержек (при практически неизменных объемах поставок) в течение последних лет. Предварительное обследование показало, что оплата перевозок осуществляется исходя из количества вагонов, времени их использования, а также зависит от типов используемых вагонов, общего суточного вагонооборота комбината. Дополнительные издержки могут быть вызваны задержками вагонов по вине грузополучателя и обусловлены чрезмерной загруженностью фронтов погрузки-выгрузки, отсутствием ресурсов, требуемых для погрузки-выгрузки, неэффективным планированием поставок, прочими причинами. Значительная часть фактических издержек приходится на штрафные санкции, применяемые к грузополучателю ОАО РЖД по причине чрезмерных непроизводительных простоев вагонов. Ситуация усугубляется ²рваным² характером процесса доставки: периодические насыщения системы чередуются с периодами простоя фронтов, что приводит к росту альтернативных издержек. Все это свидетельствует о неэффективности организации и планирования транспортного процесса и необходимости разработки и принятия мер по его оптимизации. Эффективная организация перевозок может быть определена как задача построения графика доставок грузов транспортными средствами заданной грузовместимости, которые должны осуществлять перевозку продукции от некоторого числа поставщиков единственному клиенту ЧЭМК с известными потребностями и пропускной способностью. Расписание поставок следует формировать так, чтобы минимизировать функцию цели (суммарные транспортные издержки) при существующих ограничениях (пропускной способности пунктов разгрузки вагонов, продолжительности работ фронтов погрузки-выгрузки, прочие условия). Тогда задача организации перевозок может быть сформулирована следующим образом: построить математическую модель, описывающую реальный процесс доставки грузов с учетом допущений, формализовать критерии оптимальности и накладываемые ограничения, реализовать разработанную модель в виде программного модуля, позволяющего оператору планировать и оптимизировать процесс доставки грузов. Принятые допущения Математическая модель описывает реальные процессы рассматриваемой предметной области с некоторым упрощением. Степень этого упрощения определяется вводимыми допущениями. 1) Процессы обмена передаточными составами со станциями комбината, расформирования передаточных вагонов, поступающих с дороги, формирования составов для передачи их на имеющиеся фронты погрузки-выгрузки не рассматриваются. 2) Считаем, что ситуация отсутствия свободных складских площадей невозможна. Работа фронтов не прерывается никакими другими обстоятельствами, кроме как нулевой загруженностью (отсутствием подлежащих разгрузке вагонов). 3) Порожние вагоны более не используются и после выгрузки возвращаются владельцу. Процесс отправки порожних вагонов не препятствует доставке вагонов для разгрузки. 4) Время доставки вагонов от приемных станций до фронтов погрузки-выгрузки пренебрежимо мало в сравнении со временем, требуемым для разгрузки партии вагонов. 5) Время разгрузки вагона зависит только от его типа и не зависит от вида перевозимой в нем продукции. 6) Каждый поставщик занимается поставкой только одного вида сырья в одном типе вагонов. Принятые обозначения При построении математической модели примем следующие обозначения: k – номер фронта выгрузки, k = 1, 2, …, K, где K – количество фронтов выгрузки; Fk – пропускная способность k-го фронта; z – тип вагона, z = 1, 2, …, Z, где Z – количество используемых типов вагонов; n – вид груза, n = 1, 2, …, N, где N – количество видов грузов; hz – характеристика транспортных издержек вагонов z-го типа; H(t) – функция транспортных издержек; Yz – время, требуемое для разгрузки z-го типа вагонов, [час]; Pn – годовая потребность n-го вида груза, [тонна]; An – тип используемого вагона под n-й вид груза; Rh – количество рабочих часов в сутки, [час/сутки]; Rd – количество рабочих дней в год, [день/год]. Knz – вместимость груза типа n в вагон типа z, [тонна/вагон]. Функция поставок грузов Пусть X(t) – матричная функция поставок дискретного аргумента t (сутки). Для каждого t функция возвращает матрицу-строку X размерности 1•Z, такую что X[z] – это количество вагонов типа z, подлежащих разгрузке на момент времени t. Например,
означает, что за второй рабочий день мы должны разгрузить 30 вагонов типа 1; 21 вагон типа 2; 15 вагонов типа 3 и 46 вагонов типа 4. X(t) складывается из двух слагаемых: X1(t) – объем груза (количество вагонов), прибывшего за t-й день; X2(t) – объем груза, оставшегося c прошлого рабочего дня; X(t)=X1(t)+X2(t), (1) где X2(t) < X(t-1). Функция загруженности системы Введем функцию загруженности W(t) дискретного аргумента t (в сутках), которая возвращает количество времени, требуемого для разгрузки имеющегося на момент времени t груза. Функция W(t) может быть найдена как: W(t)=X(t)×Y, (2) где Y – матрица-столбец размерности Z×1, такая, что Y[z] – это время (в часах), требуемое для разгрузки одного вагона типа z. Y – пропускная способность системы:
где F – матрица-столбец размерности Z×1, такая, что F[z] – это пропускная способность системы по z-му типу вагонов. Суммарная пропускная способность системы:
График функции загруженности имеет вид гистограммы (рис. 1).
1) нагрузка на систему соответствует ее возможностям по разгрузке доставляемых вагонов; 2) нагрузка на систему меньше ее пропускной способности. В этом случае можно говорить о непроизводительных простоях и, как следствие, об альтернативных издержках; 3) нагрузка на систему превышает пропускную способность системы. В таких случаях некоторый объем работы X2 (остаток) переносится на следующий день, а транспортные издержки, вызванные дополнительными простоями вагонов, возрастают по нелинейному закону. Для описания загруженности системы с уже распределенными остатками введем функцию W*(t):
Так как каждый тип вагона обладает своей характеристикой издержек, функцию загруженности системы также целесообразно представить в виде суперпозиции загруженности по каждому типу вагонов.
Загруженность по z-му типу вагонов на t-й день рассчитывается по формуле:
Характеристики издержек для различных типов вагонов Каждый тип вагона имеет свою характеристику издержек, задаваемую поставщиком услуг по транспортировке и представляемую обычно в табличной форме. В разрабатываемой модели эту характеристику будем описывать функцией hz(τ). Это функция позволяет определить размер издержек (в рублях), вызванных простоем одного вагона заданного типа в течение τ часов. Функции hz(τ), Функция транспортных издержек системы Зная загруженность системы, ее пропускную способность, характеристики издержек по всем типам вагонов, можно найти суммарные транспортные издержки системы. Введем функцию H(t) дискретного аргумента t (в сутках), возвращающую транспортные расходы (в рублях) за t-й день. Функция H(t) может быть рассчитана по формуле:
где Hz(t) – транспортные издержки по z-му типу вагонов за t-й день. Точно определить значение Hz(t) нельзя, так как неизвестно точное время поставок. Поэтому оценим максимальное значение Hz(t), возможное в случае, если все поставки X(t) пришли в начале рабочего дня (и, следовательно, простояли дольше). В этом случае процесс разгрузки вагонов типа z будет иметь вид, представленный на рисун- ке 2. Из рисунка видно, что каждый час разгружается Sz вагонов, где То есть первые Sz вагонов простояли 1 час, вторые Sz вагонов простояли 2 часа и так далее до разгрузки всех вагонов (момент времени Wz(t)). Тогда издержки по этому типу вагонов составят Sz*hz(1) + Sz*hz(2) + … Sz*hz(Wz(t)) или
Возвращаясь к суммарным издержкам за одни сутки, имеем:
Тогда суммарные издержки грузополучателя за период времени (t1; t2) могут быть найдены как площадь под кривой Hz(t):
Объемы суммарных транспортных затрат можно представить как сумму двух составляющих: H(t)=H1(t)+H2(t), (13) где H1(t) – это вынужденные затраты, связанные собственно с оплатой процесса транспортировки груза, иначе говоря, это та составляющая затрат, уменьшить которую нельзя без уменьшения объема поставок; H2(t) – это затраты, связанные с неэффективной организацией транспортного процесса и воздействием на систему возмущающих воздействий (перебои с поставками, непредвиденные расходы и т.д.). Тогда целевую функцию системы можно представить в виде: H2(t)®0. (14) Однако такое представление не имеет практического смысла, поскольку оценить H2(t) в символическом виде не представляется возможным. С другой стороны, очевидно, что система будет близка к выполнению условия (14), если функция загруженности W(t) будет близка к некоторому идеальному варианту, где функция W(t) описывает идеально равномерный по объему процесс доставки груза. Значение I (средний объем работ в часах) можно оценить следующим образом.
U[n]=Pn. (15) Тогда суммарный объем поставок (в вагонах соответствующих типов) может быть найден как (UG)T. Где G – матрица перехода от потребностей, выражаемых в тоннах груза, к потребностям в вагонах соответствующего типа. Матрица G имеет размерность N×Z и может быть вычислена по следующему закону:
Зная суммарный объем поставок, найдем общий объем работы по разгрузке, выраженный в часах:
Тогда средний ежедневный объем работ в часах:
В реальных условиях загруженность системы отклоняется от “идеального” графика. Новая целевая функция будет отражать степень отклонения реальной функции загруженности системы от идеального варианта:
Ограничение на возможность физического выполнения работы:
Минимизация целевой функции может быть достигнута только путем оптимизации расписания поставок. Задача составления расписания относится к классу комбинаторных задач. Размерность реальной задачи и нелинейность некоторых используемых в задаче характеристик не позволяет решить ее точными методами. Для решения подобных задач в приемлемое для оперативного планирования время необходимо использовать эвристические алгоритмы и средства вычислительной техники. Процесс оптимизации расписания (а следовательно, и минимизации целевой функции) можно представить в виде итеративного процесса. На входе имеется некоторое расписание (базовый план поставок). В каждой итерации промежуточное решение оценивается в соответствии с критериями оптимальности. В случае неприемлемости промежуточного решения расписание модифицируется по некоторым эвристическим алгоритмам, и новое решение вновь оценивается. Модификацию расписания может проводить как программа, так и человек-оператор. Процесс поиска решения оканчивается при выполнении одного из следующих условий: · · достигнут предел по количеству итераций; · последовательность модификации не привела к улучшению результатов в соответствии с критериями оптимальности. Сформулированная математическая модель имеет ряд особенностей, усложняющих поиск оптимального решения: - нелинейность использующихся в модели законов и процессов; - целочисленность некоторых параметров и функций; - многомерность задачи; - стохастистичность процессов. Для упрощения процесса поиска оптимизированного решения этот процесс следует алгоритмизировать и реализовать программно. Благодаря автоматизации процесса оператор способен в кратчайшие сроки формировать планы поставок, удовлетворяющие требованиям предприятия (плану производства), оптимизировать транспортный процесс. К программе были выдвинуты следующее требования: · преобразование входных данных в выходные (графики загруженности, итоговые числовые значения совокупных затрат и т.д); · проверка корректности и согласованности вводимых пользователем входных данных; · проверка расписания, отредактированного оператором, на соответствие потребностям в грузах; · требование к генерации базового расписания, поскольку процесс поиска решений предполагает наличие некоторого базового решения, поступающего на вход итеративного алгоритма; · требования к оптимизации расписания: шаги оптимизации могут осуществляться как оператором, так и программой; критерий оптимальности алгоритма – минимум совокупных издержек; методы оптимизации – перемещения поставок во времени (сдвиги) и изменения объемов отдельных поставок (перераспределения); · требования к графическому интерфейсу, который должен быть простым, единообразным и интуитивно понятным. · требования к сохранению/загрузке данных: в программе должна существовать возможность оперативного сохранения/загрузки введенных оператором данных и полученных результатов по запросу оператора. Взаимосвязанная структура входных данных представлена на рисунке 3. К выходным данным относятся: 1) Числовые и графические результаты моделирования: – графики загруженности системы; – графики издержек по крайнему оптимистическому и крайнему пессимистическому прогнозам; – совокупные транспортные издержки за рассматриваемый период. 2) Составленное и/или оптимизированное расписание поставок. Реализация программного продукта потребовала разработки таких алгоритмов, как: · алгоритм формирования списка поставок за один указанный день; · алгоритм формирования расписания (чем ближе реальный закон распределения загруженности во времени к равномерному, тем ниже будут издержки, вызванные непроизводительным простоем транспорта); · алгоритм уточнения даты поставки (позволяет анализировать загруженность системы в окрестности предварительно выбранной даты и при необходимости переносить поставку в более разгруженное место, делая тем самым совокупную динамику загруженности более равномерной); · алгоритм шага оптимизации расписания. Разработанная математическая модель и реализованный на ее основе программный модуль позволяют оптимизировать расписание поставок (минимизировать издержки на погрузку-выгрузку) при значительном сокращении времени работы специалиста отдела материально-технического снабжения. Для получения оптимального расписания поставок оператору предлагается последовательно выполнить следующие действия. 1) Описать параметры модели (ввести входные данные): · типы вагонов (пункт главного меню “Данные → Типы вагонов”); · характеристики издержек (Данные → Издержки); · грузы (Данные → Грузы): необходимо для каждого вида груза ввести потребность, объем минимальной партии, конкретный тип вагона и указать вместимость груза для выбранного типа вагона. · фронты (Данные → Фронты): необходимо ввести наименование и пропускную способность для каждого вида груза; · параметры: необходимо выбрать начальную и конечную даты, в пределах которых будут распределены поставки и коэффициент оптимистичности прогноза. Пессимистичный сценарий. Все поставки пришли одновременно в начале рабочего дня. Во время разгрузки наиболее приоритетных поставок остальные поставки непроизводительно простаивали. Оптимистичный сценарий. Новые поставки приходят как раз в моменты освобождения мощностей системы (окончания разгрузки предыдущих партий). Для вычисления оценки прогнозов, приближенной к реальности, программа в качестве входных данных получает степень оптимистичности прогнозов, которую оператор может оценить самостоятельно, например, исходя из имеющейся статистики выполнения договоров и своевременности поставок. Для получения прогнозируемых результатов с учетом степени оптимистичности прогнозов используется следующая формула:
где При К = Kmax/2 формула вырождается в среднее арифметическое: Hпрог=(Hопт+Hпесс)/2. 2) Сформировать базовое расписание: вручную – выбрав в меню <Расписание> пункт <Редактировать>; автоматически – выбрав в меню <Расписание> пункт <Сгенерировать базовое>. 3) Выполнить требуемое количество шагов оптимизации (вручную или в автоматическом режиме, выбрав Расписание → Оптимизировать). Достигнутая оптимизация не является верхним пределом. Эффективность оптимизации зависит от количества применяемых шагов оптимизации и навыков оператора. Несмотря на то, что программная разработка была сделана для ЧЭМК, она является достаточно универсальной и может применяться на многих предприятиях при указанных выше ограничениях. В частности, разработка используется на заводе ОАО ²Кузнецкие ферросплавы² (г. Новокузнецк). |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=488 |
Версия для печати Выпуск в формате PDF (1.18Мб) |
| Статья опубликована в выпуске журнала № 4 за 2005 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Система моделирования и оценки эффективности торговых стратегий
- Интегрированная система «микросреда»
- Основные характеристики методики АДЕСА-2 для разработки информационных систем и возможности ее практического применения
- Место XML-технологий в среде современных информационных технологий
- Системы баз данных и знаний, разработанные в Республике Куба
Назад, к списку статей



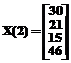
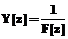 , (3)
, (3)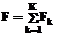 . (4)
. (4)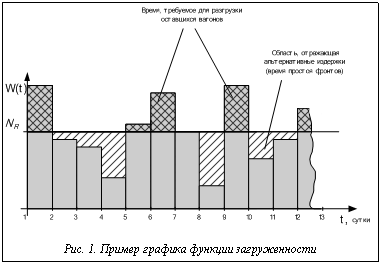 Из рисунка видно, что ежедневно может складываться одна из трех возможных ситуаций:
Из рисунка видно, что ежедневно может складываться одна из трех возможных ситуаций: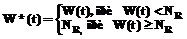 . (5)
. (5)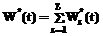 . (6)
. (6)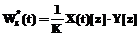 . (7)
. (7)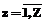 обладают следующими общими свойствами: все функции являются неубывающими и в общем случае нелинейными. Нелинейный вид семейства функций hz(τ),
обладают следующими общими свойствами: все функции являются неубывающими и в общем случае нелинейными. Нелинейный вид семейства функций hz(τ),  , (8)
, (8) . (9)
. (9) . (10)
. (10)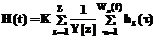 . (11)
. (11)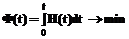 . (12)
. (12)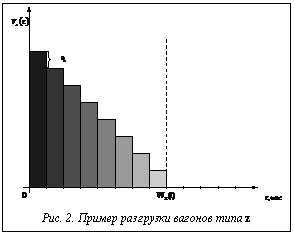 Пусть U – матрица-строка размерности 1×N, описывающая потребности в грузах (в тоннах) за период времени Δt,
Пусть U – матрица-строка размерности 1×N, описывающая потребности в грузах (в тоннах) за период времени Δt, (16)
(16)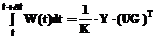 . (17)
. (17) . (18)
. (18)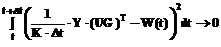 . (19)
. (19)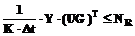 . (20)
. (20)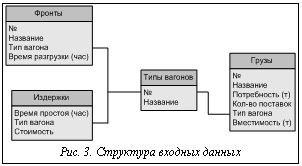 достигнут требуемый уровень оптимальности решения;
достигнут требуемый уровень оптимальности решения;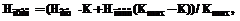
 .
.