Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Моделирование структуры сети авиамаршрутов предфрактальными графами
Аннотация:В работе выделены основные направления исследования: проектирование сети с заданными численными характеристиками, расчет устойчивости заданной сети и решения, решение оптимизационных многокритериальных задач со многими параметрами, моделирование динамических сетей. Структура сетей иерархическая, с высокими параметрами кластеризации, обладает свойствами самоподобия на уровне глобальных авиаперевозок. Сети воздушного движения относят к типу безмасштабных сетей, или «маленького мира», а для анализа применяется теория сложных сетей. В качестве инструментария решения оптимизационных задач предложен аппарат предфрактальных графов, приведены основные определения и обозначения, рассмотрены динамические правила порождения графов. Для решения NP-полных задач, встречающихся в транспортно-логистических системах, может быть применен метод, снижающий трудоемкость для ряда подзадач. Рассмотрена модель покрытия сети авиамаршрутов предфрактальным графом, предложена постановка многокритериальной задачи размещения кратного центра со многими весами, проведена оценка радиальной метрики. Предложен алгоритм размещения кратного центра предфрактального графа при сохранении смежности старых ребер, сгенерирован граф и выделены вершины кратного центра. Правила порождения предфрактального графа позволяют генерировать сети с заранее за-данными характеристиками, такими как центральность вершин, диаметр и др., в том числе для по-строения авиамаршрутов, размещения аэропортов и пересадочных узлов. Перспективными направлениями дальнейших исследований являются распознавание реальных сетей авиамаршрутов в виде динамических графов, взвешивание многими весами и постановка оптимизационных многокритериальных задач, анализ структурных характеристик сетей, статистический анализ на основе малых структурных элементов сети, генерирование сетей с заданными свойствами и сравнение их с реальными сетями, анализ структурной устойчивости сетей и др.
Abstract:The paper highlights the main research areas: designing a network with given numerical characteristics, calculating the stability of a given network and a solution, solving optimization multicriteria problems with many parameters, and modeling dynamic networks. The structure of networks is hierarchical, with high clustering parameters; it has the properties of self-similarity at the global air transportation level. Air traffic networks are referred as scaleless net-works or “small world” type. Their analysis involves using the theory of complex networks. The au-thors propose the apparatus of prefractal graphs as a tool for solving optimization problems. They also give basic definitions and notations, consider dynamic rules for generating graphs. In order to solve NP-complete problems in transport and logistics systems, it is proposed to use a method that reduces the complexity for a number of subtasks. The paper considers a model for covering an air route network with a prefractal graph, proposes to state a multicriteria problem of locating a multiple center with many weights, and gives a radial metric estimate. There is a proposed algorithm for placing a prefractal graph multiple center while maintaining the adjacency of old edges. Therefore, the authors generate a graph and select the multiple center verti-ces. The rules for generating a prefractal graph make it possible to generate networks with predeter-mined characteristics, such as vertex centrality, diameter, etc., including those for building air routes, locating airports and transfer hubs. The promising directions of further research are the recognition of real aircraft networks in the form of dynamic graphs, weighing by many weights and formulation of optimization multicriterial tasks, analyzing network structural characteristics, a statistical analysis based on small network structural el-ements, generating networks with specified properties and comparing them with real networks, analyz-ing structural stability of networks, etc.
| Авторы: Кочкаров Р.А. (rasul_kochkarov@mail.ru) - Финансовый университет при Правительстве РФ (доцент), Москва, Россия, кандидат экономических наук | |
| Ключевые слова: структура сети воздушного движения, предфрактальных граф, многокритериальная задача, радиальная метрика |
|
| Keywords: air traffic network structure, prefractal graphs, multicriteria problem, radial metric |
|
| Количество просмотров: 1328 |
Статья в формате PDF |
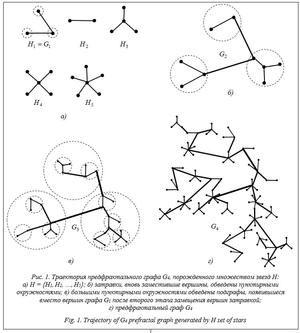
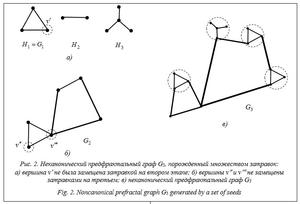
Для анализа структуры сетей авиамаршрутов в крупных регионах определяется плотность воздушного движения с помощью эконометрической гравитационной модели, которая состоит из ВВП, численности населения, расстояния и других переменных. Также исследуется зависимость числа деловых связей между городами и количеством авиамаршрутов [1]. Так как в исследовании структуры пассажирских и грузовых перевозок разделены, следует определить связи на модельном уровне. Важным вопросом является формирование сети воздушного движения, способной выдерживать отказы аэропортов и отмены маршрутов из-за сложных погодных условий, сбоев в программном обеспечении, нехватки оборудования, наземных задержек и других аварийных событий. В этом контексте одной из задач является проектирование сети авиамаршрутов с сохранением надежности и устойчивости при добавлении одного или нескольких маршрутов. Измерять и оптимизировать надежность сети воздушного движения можно с помощью метода максимизации энергии Лапласа [2]. Этот метод рассматривается как один из видов энтропии графа, который в отличие от алгебраической связности также использует локальные характеристики сети. Для исследования структуры сети воздушного движения применяется теория сложных сетей [3], авиационная сеть по сути представляет собой иерархическую структуру [4]. Анализ структуры авиатранспортной сети проводится с помощью коэффициентов кластеризации, центральности, близости и промежуточности вершин. Следует отметить, что сети с плотной взаимосвязью более устойчивы к изменениям [5]. Сети авиамаршрутов также представляют собой безмасшатбные сети, или «малые миры», в которых степени вершин распределены по степенному закону. Вместе с тем для сетей авиамаршрутов проводятся в основном статистические исследования. Структурно-топологическим вопросам, проектирова- нию сетей с заданными характеристиками, теоретико-графовому моделированию уделено меньше внимания. Проблема оптимизации потока в сети воздушного движения представляет собой двухкритериальную задачу построения оптимального плана полетов для всех запланированных рейсов в течение заданного периода времени (1–24 ч) на основе последней известной информации о пропускной способности [6]. Эта задача также принадлежит классу NP-трудных и требует специальных методов решения. Другим подходом является статистический анализ графовых характеристик сети воздушного движения, на основе которого строится прогноз загруженности сети и точек отказа [7]. Также для анализа сложности сети используют такую характеристику, как центральность, которая отражает важность узла [8, 9]. Отдельно рассматриваются масштабы сети воздушного движения, локальные, региональные и международные. Эти типы сетей, с одной стороны, имеют схожую архитектуру, с другой, свои особенности. Следует отметить новый комплексный подход к анализу сети для определения загруженности воздушного движения на основе анализа локальных элементов. Фактически сеть моделируется двух- и трехвершинными подграфами, для которых применяются известные методы анализа [10]. Во всех работах сети рассматриваются в контексте использования крупномасштабных, в современной терминологии – больших данных, формируемых в процессе слежения за воздушным трафиком [11]. В работах последних лет большое внимание уделяется динамике поведения сетей и связанных процессов [12]. Например, на основе сети воздушного движения США предлагается конструирование динамического графа, отражающего распространение задержек в сети, а также метрические показатели для измерения динамики распространения задержки [13]. Для решения NP-полных задач, встречающихся в транспортно-логистических системах, может быть применен метод, снижающий трудоемкость для ряда подзадач [14]. Методы многокритериальной оптимизации на многовзвешенных динамических графах с детерминированными весами дают возможность ре- шения задач в сложноструктурированных сетях [15], в том числе с финансово-экономическими показателями [7, 16]. В дальнейших исследованиях необходимо уделить внимание декомпозиции сетей, стати- стическому анализу малых структурных эле- ментов, а также возможностям параллельных вычислений для получения быстрых решений сложных задач [17]. Публикации последних лет посвящены динамическим свойствам сетей и в целом использованию инструментария теории динамических графов [18, 19]. Отдельно следует отметить задачи оптимального развития динамической транспортной сети [20]. В сфере авиационных перевозок решается множество частных и более масштабных задач. Для этого используются различные инструменты. Тем не менее все эти задачи могут решаться в связи друг с другом, для чего возможно построение комплексной модели, состоящей из взаимосвязанных моделей. Таким образом, можно выделить ряд направлений исследований: - проектирование сети с заданными численными характеристиками (загруженность аэропортов, трасс, самолетов, время полета, количество пересадок, стоимость перелета и т.д.); проектирование сети с заданными структурными характеристиками (структурная устойчивость, центральность, диаметр и др.); - расчет устойчивости заданной сети и решения в случае отказов составляющих ее элементов, имитационное моделирование и выделение возможных сценариев; - решение оптимизационных многокритериальных задач со многими параметрами (снижение расходов, максимизация общего полетного времени, минимизация простоя самолета или парка самолетов и др.); - моделирование динамических сетей, получение динамических решений, адаптируемых к текущей обстановке. Предфрактальные графы и оптимизационные задачи Структуры таких сложных систем, как информационные, электроэнергетические, коммуникационные, Интернет и представленные выше сети авиамаршрутов, по истечении времени претерпевают определенные изменения в силу различных внешних обстоятельств. Структуру системы произвольной природы (социальной, социально-экономической, технической, химико-биологической и т.п.) можно представить в виде графа. Изменения, происходящие в структуре сложной системы, могут быть описаны простейшими теоретико-графо- выми операциями: стягивание ребра, удаление (добавление) ребра, удаление (добавление) вершины. Изменения структуры системы могут быть и разовыми, и постоянными. Для второго случая вводится понятие структурной динамики – изменение структуры системы с течением времени. Несомненно, для описания структурной динамики более всего подходит аппарат динамических графов. Одним из самых распространенных сценариев структурной динамики является рост структуры – регулярное появление новых элементов и связей в структуре системы. Рост структуры может происходить по строго сформулированным правилам, не исключая наличия в них фактора случайности. В настоящей работе рассматривается одно из возможных правил, задающих структурную динамику сложных систем. Формальным представлением изменения структур систем по этому правилу являются самоподобные графы (self-similar graphs) большой размерности, называемые предфрактальными. Для обозначения графа используется общепринятое обозначение G = (V, E). Для пред- фрактальных графов далее приводятся некоторые дополнительные определения и обозначения. Затравкой называется связный n-вершинный граф H = (W, Q) c непомеченными вершинами. Обобщением известной операции расщепления вершины графа является операция замещения вершины затравкой. Суть этого обобщения состоит в том, что расщепляемая вершина замещается не ребром, а затравкой H. Предфрактальный граф обозначается через GL = (VL, EL), где VL - множество вершин графа, а EL - множество его ребер. В построенном на предыдущем этапе l = 1, 2, …, L–1 графе Gl каждая вершина заменяется затравкой H. На этапе l = 1 предфрактальному графу G1 соответствует затравка H = G1. Процедура порождения предфрактального графа GL также называется порождением затравкой H. Процесс порождения GL есть процесс построения последовательности G1, G2, …, GL, называемой траекторией предфрактального графа. Обобщением процесса порождения является случай, когда вместо единственной затравки H задается множество затравок H = {H} = {H1, H2, …, HT}, T ³ 2. При переходе от графа Gl–1 к графу Gl вершины замещаются одной из затравок множества H = {H}, которая выбирается случайно или согласно правилу моделируемой задачи [21]. Далее рассматриваются только неориентированные графы, для ориентирован- ных требуются дополнительные исследования. На рисунке 1 представлен процесс порождения предфрактального графа G4, порожденного множеством звезд H = {H1, H2, …, H5}, смежность старых ребер выбрана произвольной. Отличительной особенностью процесса порождения предфрактального графа является то, что на каждом этапе l = 2, 3, …, L в текущем графе Gl–1 затравкой замещается каждая вершина. Предфрактальные графы, получаемые в результате такого процесса, называем каноническими. В общем случае неканонический предфрактальный граф порождается множеством затравок H, где при переходе от графа Gl–1 к графу Gl в траектории затравкой замещается не каждая вершина, а лишь подмножество вершин, которое определяется согласно правилам, отражающим содержательную специфику моделируемой задачи.
Покрытие карты авиамаршрутов предфрактальным графом Движение самолета из пункта A в пункт B задается двумя вершинами и ребром графа. Зафиксировав карту авиамаршрутов на отдельный промежуток времени, в течение которого она не меняется, получим граф большой размерности. В предположении, что такой граф является предфрактальным, в качестве элементов порождающего множества затравок применяются преимущественно звезды с разным количеством концевых вершин (см. http://www. swsys.ru/uploaded/image/2022-1/2022-1-dop/16. jpg). Для построения предфрактального графа, а фактически для его распознавания, используются известные алгоритмы распознавания фрактальных графов [22]. Результатом распознавания является предфрактальный граф GL, порожденный множеством затравок H = {H}, где H – преимущественно звезды. Многокритериальная задача размещения кратного центра Для решения одной из задач оптимального составления плана полетов предлагается поста- новка многокритериальной задачи размещения p-центра. Рассматривается предфрактальный граф GL = (VL, EL), порожденный множеством затравок H = {H}. Каждому ребру e(l) Î EL при- писано M действительных чисел wi(e) = = wi(e(l)) Î (ql–1a, ql–1b), Пусть x - подмножество, состоящее из p вершин множества VL. Через d(x, vi) обозначается наикратчайшее из расстояний между вершинами множества x и вершиной vi, то есть Всевозможные p-центры {x} образуют множество допустимых решений X = X(GL) = {x}. На множестве x определена векторно-целевая функция: F(x) = (F1(x), F2(x), …, F2M+2(x)), Fi(x) = si(x) ® min, где si(x) – число разделений множества x по i;
где rit – радиус t-вершины p-центра по i; F2M+2(x) = ħ ® min, ħ – количество типов центров; F2M+2(x) = p ® min, p – количество вершин, составляющих p-центр. Все критерии векторно-целевой функции F(x) имеют конкретную содержательную интерпретацию. Веса, приписанные ребрам предфрактального графа GL, отражают как конкретные ограничения (время, расстояние), налагаемые на систему служб, так и общие затраты, выражаемые в условных единицах. На практике число разделения si(x) означает расстояние от самого далекого аэропорта до системы служб. Все M веса одного ребра считаются несравнимыми, в противном случае была бы применена свертка в один вес. Тогда паретовское множество включает в себя p-центры каждого набора из M весов. Критерий Fi(x) миними- зирует число разделения, а FM+i(x) – сумму радиусов p-центра по i‑му набору весов, где Оценка радиальной метрики Длина кратчайшего пути, соединяющего пару вершин w, v Î W, называется расстоянием между вершинами w, v и обозначается через d(w, v). Величина Рассмотрим предфрактальный граф GL, порожденный затравкой-звездой H, всем ребрам которого приписан вес, равный единице (коэффициент подобия равен 1). Вычислим верхние и нижние оценки радиуса предфрактального графа Gl, Радиус графа G1 равен единице, так как G1 = H есть затравка-звезда: r(G1) = 1. Центром графа G1 является вершина, смежная со всеми остальными вершинами. Расстояние от центра до любой другой вершины равно единице. В случае, если смежность старых ребер графа G2 сохраняется, радиус rmin(G2) = 2. Если старые ребра не пересекаются и инцидентны висячим вершинам подграф-затравок, радиус rmax(G2) = 4. Верхняя и нижняя оценки радиуса предфрактального графа G2 с произвольной смежностью старых ребер равны: 2 £ (G2) £ 4. По аналогии с предыдущими вычислениями верхняя и нижняя оценки радиуса графа G3 равны: 3 £ (G3) £ 13.
Продолжая процесс вычисления, получаем верхние и нижние оценки радиуса предфрактального графа Gl, rmin(G1) = 1; rmax(G1) = 1; rmin(G2) = 2; rmax(G2) = 3 + 1; rmin(G3) = 3; rmax(G3) = 32 +3 + 1; …………………………………………………… rmin(Gl) = l;
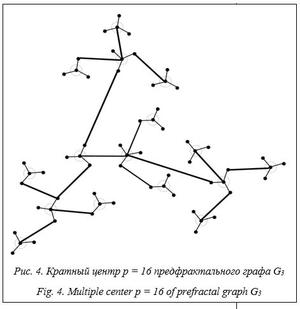
…………………………………………………… rmin(GL) = L; Тогда верна следующая теорема. Теорема 1. Для всякого предфрактального графа Gl, порожденного затравкой-звездой, радиус l £ (Gl) £ (3l – 1)/2 для всех Верхние и нижние оценки диаметра пред- фрактального графа Gl, dmin(G1) = 2; dmax(G1) = 2; dmin(G2) = 4; dmax(G2) = 2(3 + 1); dmin(G3) = 6; dmax(G3) = 2(32 +3 + 1); …………………………………………………… dmin(Gl) = 2l; …………………………………………………… dmin(GL) = 2L; Тогда верна следующая теорема. Теорема 2. Для всякого предфрактального графа Gl, порожденного затравкой-звездой, диаметр 2l £ d(Gl) £ 3l – 1 для всех Примечание. Оценки радиуса l £ r(Gl) £ £ (3l – 1)/2 и диаметра 2l £ d(Gl) £ 3l – 1 верны для всякого предфрактального графа Gl, Алгоритм размещения кратного центра предфрактального графа Рассмотрим предфрактальный граф GL при сохранении смежности старых ребер. Затравка H является связным графом, и каждая ее вершина достижима из всякой другой вершины. Алгоритм применяется для одного фиксированного набора весов wi(e) из M и далее обобщается для каждого i‑го набора, Алгоритм al позволяет построить p-центр предфрактального графа для p = nl вершин, где l Î [1, L – 1]. Алгоритм работает на блоках Алгоритм al. Вход: взвешенный предфрактальный граф GL. Выход: p-центр GL. Для всех s = 1, 2, …, nl выполнить: Шаг 1. Последовательно для каждого s-го блока Шаг 2. На выходе шага 1 получено nl центров блоков (L – l)-го ранга. Объединение этих центров составляет p-центр xl предфрактального графа GL. Процедура поиска центра. Вход: взвешенный граф G. Выход: центр графа. Теорема 3. Алгоритм al выделяет p-центр xil, Алгоритм al позволяет размещать кратный центр по каждому из M наборов весов. Теорема 4. Вычислительная сложность алгоритма al равна O(4n2NM). Теорема 5. Алгоритм al выделяет р-центр xil, l Î [1, L – 1], на предфрактальном графе GL, оптимальный по критериям На рисунке (см. http://www.swsys.ru/uploaded/image/2022-1/2022-1-dop/17.jpg) сгенерирован взвешенный предфрактальный граф G3, порожденный полной четырехвершинной затравкой, с сохранением смежности старых ребер. Двойными пунктирными окружностями выделены вершины кратного центра p = 4, l = 2. Задача решается с одним набором весов в двухкритериальной постановке – с критериями F1(x) и F2M+1(x).
Заключение Структура сетей является иерархической, с высокими параметрами кластеризации, обла- дает свойствами самоподобия на уровне гло- бальных авиаперевозок. Сети воздушного дви- жения относят к типу безмаштабных сетей, или «маленького мира», а для анализа применяется теория сложных сетей. Предложенный аппарат предфрактальных графов позволяет моделировать сети любой сложности при сохранении всех перечисленных выше особенностей. При этом для предфрактальных графов разработаны специализированные инструменты решения трудных задач. Например, для решения NP-полных задач, встречающихся в транспортно-логистических системах, может быть применен метод, снижающий трудоемкость для ряда подзадач. Правила порождения предфрактального графа позволяют генерировать сети с заранее заданными характеристиками, такими как центральность вершин, диаметр и другие, в том числе для построения авиамаршрутов, размещения аэропортов и пересадочных узлов. Методы многокритериальной оптимизации на многовзвешенных предфрактальных графах с детерминированными весами позволяют решать задачи в сложноструктурированных сетях. В дальнейших исследованиях планируется уделить внимание декомпозиции сетей и статистическому анализу малых структурных элементов, а также возможностям параллельных вычислений для получения быстрых решений сложных задач. Публикации последних лет направлены на изучение динамических свойств сетей и в целом использования инструментария теории динамических графов, в связи с чем планируется исследование именно динамических свойств предфрактальных графов. Предполагаются распознавание реальных сетей авиамаршрутов в виде динамических графов, взвешивание многими весами и постановки оптимизационных многокритериальных задач, анализ структурных характеристик сетей, статистический анализ на основе малых структурных элементов сети, генерирование сетей с заданными свойствами и сравнение с реальными сетями, выявление сходства и расчет соответствующего показателя схожести сетей. Необходимо обратить внимание на динамичность сетей, постановку задач на предфрактальных графах как подклассе динамических графов, анализ структурной устойчивости сетей и устойчивости решений на них. Литература 1. Matsumoto H., Domae K., O'Connor K. Business connectivity, air transport and the urban hierarchy: A case study in East Asia. J. of Transport Geography, 2016, vol. 54, pp. 132–139. DOI: 10.1016/j.jtrangeo. 2016.05.005. 2. Yang Ch., Mao J., Wei P. Air traffic network optimization via Laplacian energy maximization. Aerospace Science and Technology, 2016, vol. 49, pp. 26–33. DOI: 10.1016/j.ast.2015.11.004. 3. Sallan J.M., Lordan O. Air transport networks and complex networks. In: Air Route Networks Through Complex Networks Theory, 2020, pp. 1–15. DOI: 10.1016/B978-0-12-812665-3.00008-6. 4. Lin J. Network analysis of China’s aviation system, statistical and spatial structure. J. of Transport Geography, 2012, vol. 22, pp. 109–117. DOI: 10.1016/j.jtrangeo.2011.12.002. 5. Sun X., Wandelt S. Network similarity analysis of air navigation route systems. Transportation Research Pt. E: Logistics and Transportation Review, 2014, vol. 70, pp. 416–434. DOI: 10.1016/j.tre.2014.08.005. 6. Xiao M., Cai K., Abbass H.A. Hybridized encoding for evolutionary multi-objective optimization of air traffic network flow: A case study on China. Transportation Research Pt. E: Logistics and Transportation Re- view, 2018, vol. 115, pp. 35–55. DOI: 10.1016/j.tre.2018.04.011. 7. Gataullin T.M., Gataullin S.T., Ivanova K.V. Synergetic effects in game theory. Proc. XIII Int. Conf. MLSD, 2020, pp. 1–5. DOI: 10.1109/MLSD49919.2020.9247673. 8. Reyna O., Mota I. Complex networks of the air passenger traffic in Monterrey´s airport. Transportation Research Procedia, 2020, vol. 48, pp. 23–31. DOI: 10.1016/j.trpro.2020.08.003. 9. Mazzarisi P., Zaoli S., Lillo F., Delgado L., Gurtner G. New centrality and causality metrics assessing air traffic network interactions. J. of Air Transport Management, 2020, vol. 85, art. 101801. DOI: 10.1016/j.jairtraman.2020.101801. 10. Jiang X., Wen X., Wu M., Song M., Tu C. A complex network analysis approach for identifying air traffic congestion based on independent component analysis. Physica A: Statistical Mechanics and its Applications, 2019, vol. 523, pp. 364–381. DOI: 10.1016/j.physa.2019.01.129. 11. Ren P., Li L. Characterizing air traffic networks via large-scale aircraft tracking data: A comparison between China and the US networks. J. of Air Transport Management, 2018, vol. 67, pp. 181–196. DOI: 10.1016/j.jairtraman.2017.12.005. 12. Li Q., Jing R. Characterization of delay propagation in the air traffic network. J. of Air Transport Management, 2021, vol. 94, art. 102075. DOI: 10.1016/j.jairtraman.2021.102075. 13. Cai Q., Alam S., Duong V.N. A spatial-temporal network perspective for the propagation dynamics of air traffic delays. Engineering, 2021, vol. 7, no. 4, pp. 452–464. DOI: 10.1016/j.eng.2020.05.027. 14. Kochkarov R. Research of NP-complete problems in the class of prefractal graphs. Mathematics, 2021, vol. 9, art. 2764. DOI: 10.3390/math9212764. 15. Кочкаров Р.А. Многовзвешенные предфрактальные графы с недетерминированными весами. Приложения в экономике, астрофизике и сетевых коммуникациях. М.: Ленанд, 2017. 432 с. 16. Gataullin T.M., Gataullin S.T. Management of financial flows on transport. Proc. XII Int. Conf. MLSD, 2019, pp. 1–4. DOI: 10.1109/MLSD.2019.8911006. 17. Головченко Е.Н. Обзор алгоритмов декомпозиции графов // Препринты ИПМ им. М.В. Келдыша. 2020. Вып. 2. С. 1–38. DOI: 10.20948/prepr-2020-2. 18. Миков А.И. Пространственная связность динамических графов в многосвязных областях // Информатизация и связь. 2020. № 2. С. 108–113. DOI: 10.34219/2078-8320-2020-11-2-108-113. 19. Kochkarov A.A., Kochkarov R.A., Malinetskii G.G. Issues of dynamic graph theory. Comput. Math. and Math. Phys., 2015, vol. 55, pp. 1590–1596. DOI: 10.1134/S0965542515090080. 20. Григоренко Н.Л., Жарков А.В., Пивоварчук Д., Попова Н.Н. Параллельный программный комплекс оптимального развития динамической транспортной сети // Программные продукты и системы. 2012. № 4. С. 54–62. 21. Кочкаров А.М. Распознавание фрактальных графов: алгоритмический подход. Нижний Архыз: CYGNUS, 1998. 170 с. URL: https://www.elibrary.ru/item.asp?id=20368135 (дата обращения: 12.12.2021). 22. Perepelitsa V.A., Sergienko N.V., Kochkarov A.M. Recognition of fractal graphs. Cybernetics and systems analysis, 1999, vol. 35, no. 4, pp. 572–585. URL: https://research.rug.nl/en/publications/recognition-of-fractal-graphs (дата обращения: 12.12.2021). References
|
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=4882&lang= |
Версия для печати |
| Статья опубликована в выпуске журнала № 1 за 2022 год. [ на стр. 113-123 ] |
Назад, к списку статей