Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Гибридная система поиска решений на основе временных продукционных правил
Аннотация:
Abstract:
| Авторы: Афонин П.В. (pavlafon@yandex.ru) - Московский государственный технический университет им. Н.Э. Баумана, Москва, Россия, кандидат технических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Всего комментариев: 1 Количество просмотров: 17694 |
Версия для печати Выпуск в формате PDF (1.41Мб) |
Большое число возникающих на практике задач обработки информации и поиска оптимальных решений требует использования методов и подходов имитационного моделирования [4,6]. При этом существует класс задач управления, в которых необходимо найти стратегию управления, переводящую систему из исходного состояния в некоторое целевое состояние. В контексте имитационного моделирования (то есть для систем, функционирование которых рассматривается на некотором временном интервале) этот класс задач можно свести к задаче нахождения некоторой оптимальной последовательности событий во времени, переводящих моделируемую систему из начального состояния в требуемое. Примерами таких задач могут служить задачи теории расписаний, исследования операций, различные транспортные задачи и пр. Задачу определения последовательности событий во времени можно отнести к классу задач поиска в пространстве состояний [7,8]. Их решение основано на использовании продукционных правил (составляющих базу знаний (БЗ) системы), которые описывают правила перевода системы из одного состояния в другое. С БЗ работает поисковый алгоритм. Его роль заключается в определении последовательности исполнения продукционных правил, при которой система переходит в целевое состояние. Однако обыкновенные продукционные правила не учитывают временной фактор, и поэтому не способны описать динамику поведения системы. Для решения рассматриваемой задачи нужно применять динамические (зависящие от времени) продукционные правила. С этой целью предложено использовать БЗ на основе модифицированных продукционных правил (МПП), которые положены в основу языка интеллектуального имитационного моделирования РДО [4]. МПП имеют вид: IF (условие) THEN (событие 1) WAIT Δt THEN (событие 2). Событие 1 и событие 2 представляют собой события начала и окончания некоторого действия, имеющего временную протяженность Δt. Длительность действия зависит от состояния ресурсов моделируемого объекта. Действие может прерываться другими действиями и событиями (главным образом случайными событиями). Стратегии поиска в пространстве состояний рассматривают различные допустимые состояния системы в процессе поиска решения. Их можно представить как нахождение пути на графе состояний от вершины, характеризующей исходную базу данных (БД) системы, к вершине, которая описывает БД, удовлетворяющую терминальному условию. Одним из наиболее перспективных методов поиска на графе является алгоритм Харта-Нильсона-Рафаэла [8], который в своей классической реализации представляет поиск на графе состояний на основе обыкновенных продукционных правил вида IF (условие) ТHEN (действие). Поиск осуществляется с помощью оценочной функции вида f(n)=g(n)+h(n), где g(n) – стоимостная составляющая оценочной функции; h(n) – эвристическая составляющая оценочной функции, задаваемая пользователем. Эвристическая составляющая – это во многих случаях набор эвристических функций h1, h2, …, hk, которые задаются экспертом. Необходимо отметить, что, как правило, используются весовые коэффициенты w1, w2, …,wk при соответствующих эвристических функциях, которые определяют взаимное соотношение эвристических функций, а также отношение эвристических функций к стоимостной составляющей оценочной функции g(n): f(n)=g(n)+w1×h1(n)+w2×h2(n)+…+wk×hk(n). При этом выбор рациональных значений весовых коэффициентов следует производить не только на начальной стадии, но и в процессе поиска решения. Даже опытному эксперту не всегда удается определить необходимую стратегию изменения значений весовых коэффициентов эвристических функций в процессе поиска на графе.
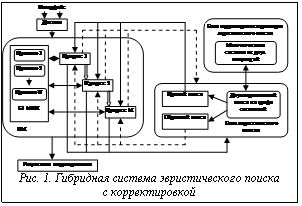
Одной из ведущих тенденций, определяющей развитие современной информатики и искусственного интеллекта, стало распространение интегрированных и гибридных систем [5,9,10]. Подобные системы обычно состоят из разнородных элементов (компонентов), объединенных в интересах достижения поставленных целей. На основе разработанного В.В. Емельяновым метода РДО [4] им и его учениками были предложены различные структуры гибридных систем, предназначенных для поиска решений с помощью имитационных моделей (ИМ) сложных систем [1-3]. В развитие подхода В.В. Емельянова рассмотрим структуру гибридной системы эвристического поиска с корректировкой (рис.1). ИМ включает в себя БЗ на основе МПП. Задачей поиска является определение последовательности выполнения МПП из БЗ, то есть составление процесса последовательности исполнения действий во времени, при котором достигается целевое состояние моделируемой системы. При этом в рамках одного прогона ИМ может быть поставлено несколько задач по составлению процесса последовательности исполнения действий. Для этого используется блок эвристического поиска, в основу которого положена стратегия поиска на графе состояний по модифицированному алгоритму Харта-Нильсона-Рафаэла, реализующему поиск решения на базе МПП. Поиск можно осуществлять как в прямом, так и в обратном направлении. Предлагаемая система имеет блок корректировки поиска на основе методов теории агентов и многоагентных систем (МАС) [9]. Он позволяет корректировать параметры однонаправленного и двунаправленного эвристического поиска, в результате чего сокращается время работы алгоритма. При этом для корректировки параметров однонаправленного поиска используется МАС, состоящая из одной популяции агентов, а для корректировки двунаправленного поиска – МАС, охватывающая две популяции агентов.
Если ни одно правило в данный момент выполнить невозможно, то происходит проверка условия блока 7: имеются ли в текущий момент имитационного времени t для состояния системы в вершине Sn запущенные на исполнение правила. Если выполняемых правил нет, то есть в текущий момент имитационного времени t не выполняется ни одно действие, то это означает, что вершина Sn породила всех своих преемников; она исключается из рассмотрения на графе состояний. При этом вершина Sn перемещается из списка OPEN в список CLOSED (блок 10). Если в момент проверки условия блока 7 имеются исполняемые правила, то происходит продвижение имитационного времени t на величину ∆t (блок 8), которая определяется имитатором системы ИМ. Если при проверке условия блока 6 выполнение какого-либо правила из БЗ возможно, то происходит порождение преемника Sk для вершины Sn, которое реализует блок 9. При этом осуществляется фиксация состояния системы для порожденной вершины Sk и добавление ее в список BUF. Для вершины Sk записывается указатель на свою вершину-родителя Sn. Порождение очередного преемника Sk вершины Sn реализуется путем исполнения очередного МПП из всех возможных и нерассмотренных правил в вершине Sn. В этот момент срабатывает первая часть исполняемого правила, то есть событие начала действия. Фиксация состояния системы в вершине означает занесение в память номера исполняемого МПП, значения имитационного времени в данной вершине, а также списка исполняемых в текущий момент МПП, для каждого из которых указывается значение времени запуска относительно текущего значения имитационного времени в данной вершине. Таким образом, каждая вершина графа G, за исключением исходной вершины, представляет собой момент начала некоторого действия во временном процессе. Данный процесс соответствует набору действий, произошедших на интервале имитационного времени при рассмотрении пути графа от целевой к текущей вершине. В блоке 11 реализуется переориентация указателей вершин списка OPEN. При раскрытии вершины Sn существует вероятность получения вершин-преемников, которые описывают ранее рассмотренные состояния БД системы в ходе поиска на графе. В общем случае неявный граф G не является деревом, и может существовать несколько вершин-родителей для одной вершины. Для сохранения древовидной структуры в явно построенном на данный момент графе G необходимо сравнить стоимости путей g(Sk) и g(Sl), описывающих одинаковые состояния БД системы в вершинах Sk и Sl, и оставить путь с наименьшей стоимостью. Для каждой вершины Sk из списка BUF производится сравнение состояний с вершинами из списков OPEN и CLOSED. Возможны два варианта: вершина Sk подобна вершине Sl из списка OPEN или очередная вершина Sk подобна вершине Sm из списка CLOSED. В первом случае, если g(Sk) < g(Sl), то вершина Sk остается, а вершина Sl удаляется. В противном случае вершина Sm остается, а вершина Sk удаляется. В блоке 12 реализуется сортировка списка OPEN, в результате которой список упорядочивается в соответствии с рассчитанными значениями оценочных функций. При этом, по сути, происходит сортировка вершин-преемников из списка BUF относительно вершин в списке OPEN. После окончания операции сортировки список BUF удаляется. МАС, моделирующая одну популяцию агентов, описывается следующим образом: MAS = , где A – множество агентов; E = {e}– среда, в которой находится МАС; R – множество взаимодействий между агентами; ACT – множество действий агентов; EV – множество эволюционных стратегий; T – множество времен жизни агентов. Параметрами модели являются: 1) размер начальной популяции N0; 2) вероятность скрещивания Pc; 3) вероятность мутации Pm; 4) время жизни ti агента ai (здесь ti – случайная величина на заданном интервале [ti1, ti2]); 5) число раскрываемых вершин n до операции смены вершины графа (переселения агента); 6) зависимость силы агента от возраста. Агент характеризуется: - генотипом, представляющим собой закодированные значения управляющих коэффициентов w1, w2, ..., wi эвристических функций; - функцией пригодности для конкретной вершины графа, которая является значением оценочной функции в данной вершине при соответствующих генах агента; - силой в конкретной вершине графа, которая зависит от функции пригодности агента и его возраста, при этом сила агента в разных вершинах различна. Предложен способ расчета силы агента в конкретной вершине графа. В результате проведенных экспериментальных исследований установлено, что использование МАС для корректировки весов эвристических функций в процессе поиска позволяет сократить время поиска на 5-20%. Список литературы 1. Емельянов В.В. Гибридные системы управления на основе интеллектуальной имитационной среды РДО // Тр. II Междунар. конф.: Проблемы управления и моделирования в сложных системах. – Самара: СНЦ РАН, 2000. – С. 263-268. 2. Емельянов В.В., Зафиров Э.Г. Гибридные системы на базе генетических оптимизационных алгоритмов и интеллектуального имитационного моделирования// Тр. YII Нац. конф. по искусствен. интеллекту КИИ’2000 (Переславль-Залесский, 24-27 октября 2000 г.). – М.: Физматлит, 2000. – Т.2. – С.780-788. 3. Емельянов В.В., Зафиров Э.Г., Штаутмайстер Т. Генетические алгоритмы в гибридных интеллектуальных системах // Интегрированные модели и мягкие вычисления в искусственном интеллекте. / Сб. тр. Междунар. науч.-практич. семинара (Коломна, 17-18 мая 2001 г.). – М.: Наука. Физматлит, 2001. – С.191-196. 4. Емельянов В.В., Ясиновский С.И. Введение в интеллектуальное имитационное моделирование сложных дискретных систем и процессов. Язык РДО. – М.: АНВИК, 1998. 5. Колесников А.В. Гибридные интеллектуальные системы. Теория и технология разработки / Под ред. А.М. Яшина. – СПб.: СПбГТУ, 2001. 6. Лоу А., Кельтон В. Имитационное моделирование. / Пер. с англ. (3-е изд.) – СПб.: BHV, 2004. 7. Люгер Дж.Ф. Искусственный интеллект. Стратегии и методы решения сложных проблем. / Пер с англ. – М.: Изд. Дом «Вильямс», 2003. 8. Нильсон Н. Принципы искусственного интеллекта. / Пер. с англ. – М.: Изд. Дом «Вильямс», 2001. 9. Тарасов В.Б. От многоагентных систем к интеллектуальным организациям: философия, психология, информатика. – М.: Эдиториал УРСС, 2002. 10. Medsker L.R. Hybrid Intelligent Systems. – Dordrecht: Kluwer Academic Publ., 1995. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=498 |
Версия для печати Выпуск в формате PDF (1.41Мб) |
| Статья опубликована в выпуске журнала № 2 за 2006 год. | Версия для печати с комментариями |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Прототип интеллектуальной системы поддержки принятия решений для управления энергообъектом
- Оптимизация структуры базы данных информационной системы ПАТЕНТ
- Алгоритмы и программное обеспечение системы обработки топопланов
- Структурно-параметрическая идентификация функций занятости и прогнозирование спроса на молодых специалистов
- Интеллектуальная система для моделирования затрат-потерь и распределения ресурсов по графическим образам
Назад, к списку статей
Comments
автор: Александр [2011-03-13 16:19:32]Я полагаю что эту статью дополнит статья которая имеет название "Методы изобретательства, с помощью которых три программиста легко могут составить такие программы для компьютера, посредством которых компьютер может изобрести много изобретений без помощи человека" эта статья изложена на в иитернете.
Оценка пользователя: 10 баллов



 Алгоритмы поиска на графе различаются также направлением поиска. Существуют прямые, обратные и двунаправленные методы поиска. Прямой поиск идет от исходного состояния и, как правило, используется тогда, когда целевое состояние задано неявно. Обратный поиск идет от целевого состояния и используется тогда, когда исходное состояние задано неявно, а целевое – явно. Двунаправленный поиск требует удовлетворительного решения двух проблем: смены направления поиска и оптимизации «точки встречи». Одним из критериев для решения первой проблемы является сравнение «ширины» поиска в обоих направлениях: при этом выбирается то направление, которое сужает поиск. Вторая проблема вызвана тем, что прямой и обратный пути могут разойтись, и чем уже поиск, тем это более вероятно.
Алгоритмы поиска на графе различаются также направлением поиска. Существуют прямые, обратные и двунаправленные методы поиска. Прямой поиск идет от исходного состояния и, как правило, используется тогда, когда целевое состояние задано неявно. Обратный поиск идет от целевого состояния и используется тогда, когда исходное состояние задано неявно, а целевое – явно. Двунаправленный поиск требует удовлетворительного решения двух проблем: смены направления поиска и оптимизации «точки встречи». Одним из критериев для решения первой проблемы является сравнение «ширины» поиска в обоих направлениях: при этом выбирается то направление, которое сужает поиск. Вторая проблема вызвана тем, что прямой и обратный пути могут разойтись, и чем уже поиск, тем это более вероятно.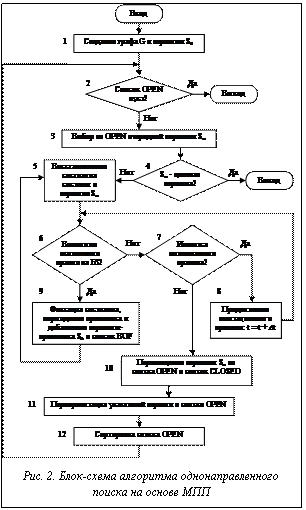 Рассмотрим блок-схему алгоритма однонаправленного поиска на графе состояний на основе МПП (рис. 2). Блок 1 реализует построение графа G, состоящего из единственной вершины S0, которая определяет исходное состояние системы. Вершина S0 заносится в список OPEN. Также создается пустой список CLOSED. В блоке 2 проверяется условие, является ли список OPEN пустым. Если список OPEN пуст, то происходит окончание работы алгоритма. В блоке 3 производится выбор очередной вершины Sn с наивысшим рангом из упорядоченного списка OPEN. Блок 4 реализует проверку условия: является ли вершина Sn целевой. Если условие выполняется, то алгоритм завершает свою работу с решением, полученным в результате прослеживания пути в графе G вдоль указателей от вершины Sn к вершине S0. В противном случае создается пустой список BUF, и алгоритм переходит к порождению вершин-преемников для вершины Sn. Блок 5 осуществляет восстановление состояния системы в вершине Sn. При этом восстанавливается состояние БД системы и значение имитационного времени, которые соответствуют данной вершине. Далее в блоке 6 проверяется, возможно ли исполнение каких-либо правил из БЗ в момент имитационного времени t, который соответствует состоянию системы в вершине Sn.
Рассмотрим блок-схему алгоритма однонаправленного поиска на графе состояний на основе МПП (рис. 2). Блок 1 реализует построение графа G, состоящего из единственной вершины S0, которая определяет исходное состояние системы. Вершина S0 заносится в список OPEN. Также создается пустой список CLOSED. В блоке 2 проверяется условие, является ли список OPEN пустым. Если список OPEN пуст, то происходит окончание работы алгоритма. В блоке 3 производится выбор очередной вершины Sn с наивысшим рангом из упорядоченного списка OPEN. Блок 4 реализует проверку условия: является ли вершина Sn целевой. Если условие выполняется, то алгоритм завершает свою работу с решением, полученным в результате прослеживания пути в графе G вдоль указателей от вершины Sn к вершине S0. В противном случае создается пустой список BUF, и алгоритм переходит к порождению вершин-преемников для вершины Sn. Блок 5 осуществляет восстановление состояния системы в вершине Sn. При этом восстанавливается состояние БД системы и значение имитационного времени, которые соответствуют данной вершине. Далее в блоке 6 проверяется, возможно ли исполнение каких-либо правил из БЗ в момент имитационного времени t, который соответствует состоянию системы в вершине Sn.