Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Инструментальная среда исследования генетических алгоритмов «GenSearch»
Аннотация:
Abstract:
| Автор: Голубин А.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 18325 |
Версия для печати Выпуск в формате PDF (0.95Мб) |
На практике часто встает задача построения таких методов оптимизации, которые были бы способны отыскивать решения практически при полном отсутствии предположений о характере исследуемой функции. Примерами таких методов являются так называемые эволюционные методы поиска и, в частности, генетические алгоритмы (ГА), моделирующие процессы природной эволюции [4, 5]. Разработано большее количество программ, использующих в той или иной мере ГА. К наиболее известным можно отнести GenAlgo, ActiveGA, Generator, Genetic Server. Большинство из существующих программ разработаны под определенные практические или исследовательские задачи, имеют ограниченный набор генетических операторов и тестовых функций, продаются по высокой цене или не предназначены к тиражированию. Стоит отметить, что большинство исследовательских программ производят тестирования на определенном наборе тестовых функций, без доказательств эффективности предложенных методик на практических задачах. Все это привело к необходимости создания инструментальной среды, которая включала бы множество генетических операторов и варьируемых параметров, позволяющих исследовать их эффективность на тестовых функциях и доказывать эффективность разработанных методик в решении практических задач. В результате была разработана инструментальная среда GenSearch. Инструментальная среда GenSearch позволяет настраивать более 20 различных параметров ГА. К основным можно отнести следующие: - размер популяции; - количество потомков; - количество поколений; - точность представления генотипа; - точность определения фенотипа; - метод выбора родительской пары; - метод отбора; - изменение метода отбора во время работы программы; - тип мутации; - вероятность мутации; - коэффициент изменения мутации; - тип кроссинговера; - метод локальной оптимизации; - количество популяций в многопопуляционном алгоритме; - способ взаимодействия популяций в многопопуляционном алгоритме; - количество запусков ГА; - настройка «встряхивания» популяции. Числовые параметры вводятся непосредственно пользователем, причем инструментальная среда контролирует корректность введенных данных. Для исследования основных генетических операций в инструментальной среде реализованы следующие их типы: метод выбора родительской пары: элитный, ближнее родство на фенотипе, дальнее родство на фенотипе, дальнее родство на генотипе, ближнее родство на генотипе; метод отбора: пропорциональный, рулетка, с вытеснением, случайный, элитный; тип мутации: инверсия, транслокация, перестановка, генная, тип кроссинговера: нет, одинарный, двухточечный, рекомбинация. Для проведения исследований и проверок гипотез и предлагаемых методик в инструментальной среде реализованы 12 тестовых непрерывных функций, а также 2 комбинаторные NP-полные задачи: коммивояжера и размещения. В инструментальной среде реализованы функции, имеющие один локальный экстремум (Розенброка, Жилинскаса, Пауэлла), функции, имеющие несколько глобальных экстремумов (Химмельблау, Растригина n=2), а также сложные многоэкстремальные функции высокой размерности (многоэкстремальная функция, функция n-переменных, Растригина n=10), имеющие как локальные, так и глобальные экстремумы и практически не решаемые классическими методами оптимизации. Для увеличения гибкости инструментальная среда позволяет проводить исследования на любой непрерывной функции, введенной пользователем. Для этого необходимо задать ограничения на переменные и выражение функции пригодности. Возможно использование промежуточных переменных. Инструментальная среда разрабатывалась не только для тестирования существующих, но и для разработки и проверки новых методик. Особое внимание стоит уделить следующим, повышающим эффективность ГА: многопопуляционный алгоритм; использование двухэтапной оптимизации; изменение вероятности мутации; «встряхивание» популяции. Многопопуляционный алгоритм [3] – это одновременное развитие нескольких популяций с различными или одинаковыми параметрами. При наступлении определенного события (через заданное количество поколений, уменьшение разнообразия в популяциях, малое изменение функции пригодности лучшей хромосомы популяции) происходит обмен между популяциями. Для этого хромосомы всех популяций объединяются в одну популяцию (общую) и одним из следующих способов распределяются между исходными популяциями. · Случайное распределение. Хромосомы для каждой популяции случайно выбираются из общей популяции. После выбора хромосома удаляется. Достоинством данного метода является простота реализации, недостатком – возможность группировки в нескольких популяциях лучших хромосом, а в остальных – худших, что приводит к уменьшению разнообразия. · Равномерное распределение на фенотипе. После объединения популяций, они сортируются по мере возрастания функции пригодности. Пусть у нас есть N популяций. В i популяцию попадут i, i+N, i+2*N, i+3*N… хромосомы. При данном подходе мы получаем разнообразие хромосом по значению функции пригодности. · Равномерное распределение на генотипе. Данный метод отличается от предыдущего тем, что сортировка происходит не на фенотипе, а на генотипе. Для увеличения разнообразия после объединения возможно добавление определенного количества случайных хромосом в общую популяцию за счет худших хромосом. Основным недостатком алгоритма является линейное увеличение временной сложности алгоритма. При двухэтапной оптимизации [1] ГА используется для быстрой локализации зоны существования экстремума, а метод локальной оптимизации – для определения более точного экстремума. В программе предлагается использование в качестве локальных следующих методов: координатного спуска, градиентного спуска, крутого восхождения, случайного поиска, метода BFGS. Повышение эффективности работы алгоритма при изменении вероятности мутации достигается за счет увеличения вероятности и, соответственно, разнообразия популяции на первоначальных этапах работы алгоритма и постепенного уменьшения на последующих. Программа позволяет пользователю устанавливать произвольный положительный коэффициент изменения вероятности мутации. Модификация популяции («встряхивание») – это удаление из текущей популяции части хромосом по определенному закону и добавление новых для повышения генетического разнообразия. Модификация производится, если лучшее значение хромосомы в популяции на протяжении нескольких поколений изменяется меньше, чем на некоторую малую величину. Для выполнения процедуры настройки ГА необходимо: 1) подобрать представление оптимизационных параметров в виде определенного формата данных: строки, вектора, таблицы и т.д.; 2) разработать или выбрать из набора генетических операторов такие, которые наилучшим образом учитывают особенности поискового пространства; 3) определить размер начальной популяции; 4) разработать методику использования генетических операторов; 5) задать функцию пригодности; 6) разработать методику отбора вариантов в новую популяцию; 7) задать критерий останова эволюционного процесса. Наиболее важным в процессе настройки ГА является выполнение пунктов 2–4 и 6. Сложность состоит в том, что, в случае неправильного выбора одного из параметров ГА, его эффективность резко снижается. В настоящее время в работах, посвященных использованию ГА для решения задач оптимизации, разработано большое количество возможных вариантов их реализации [6]. В первых исследованиях ГА использовались различные варианты комбинаций параметров ГА. Наиболее полные исследования были проведены Де Йонгом на 5 тестовых функциях, позднее ставших стандартными тестовыми функциями для исследования ГА. Для данных функций он эмпирически обнаружил следующие оптимальные параметры ГА: размер популяции 50 – 100 хромосом; кроссинговер одноточечный с вероятность 60 %; мутация битовая с вероятностью 0,1 %. Эти параметры впоследствии широко использовались в различных исследованиях и признаны как стандартное множество параметров. Другой подход к определению параметров был предложен Дебом и Агравалом. Они исследовали эффект трех параметров: размер популяции, скорость кроссинговера и мутации. Они выяснили, что алгоритмы, основанные на мутации и на кроссинговере, подходят к совершенно разным задачам – простым и сложным. Для эффективной работы их алгоритма необходим большой размер популяции. Фам предложил технику выбора параметров, основываясь на методе конкуренции между различными популяциями, использующими разные множества параметров. Несколько популяций развиваются независимо, используя свои собственные параметры. Все популяции работают на однопроцессорной машине и в зависимости от результатов получают дополнительное процессорное время. Лис ввел технику адаптации скорости мутации в модель параллельного ГА. Несколько популяций развиваются независимо на разных процессорах, используя различные скорости мутации. Через заранее определенное время эти популяции сравниваются. Если лучшие результаты были у популяции с большой скоростью мутации, то скорость мутации у остальных популяций повышается, и наоборот. Мюхленбан использовал сравнение между подпопуляциями с различными параметрами. Размер каждой подпуляции варьировался, тогда как общий размер оставался фиксированным. Каждая подпопуляция соперничала с другими за увеличение размера. Размер лучшей группы после каждого шага увеличивался, тогда как остальных уменьшался. С помощью инструментальной среды, были проведены исследования на тестовых непрерывных функциях и комбинаторных задачах. Для исследования были выбраны тестовые функции, характеризующиеся различным количеством оптимизируемых параметров, числом экстремумов как локальных, так и глобальных, видом области поиска. Цель исследований – накопление достаточного опыта для подбора параметров ГА, обеспечивающих наиболее эффективное решение оптимизационной задачи. 1. Функция Розенброка: F(х1, х2)=100*(х2-х1)2 + (1-x1)2. Ограничения: -10£ xi £10, i=1,2. Минимум: F(х*)=0. 2. Функция Жилинскаса: F(x1, x2) = x12 + x22 – cos(18x1) – cos(18x2). Ограничения: 0£ xi £ 2p, i=1,2. Минимум: F(x*) = 2. 3. Многоэкстремальная функция: F(x1…x8)=[(x1–2)2+(x2–1)2+5h2–g2x1x2me-t]/9.3741. h=(x1–2.03314x2+1.0541)/(1+m), m=x3x42 x53 x64 x75 x86, g = 0.0016/(0.01 + m12),
m1=|-x1–1.3x2+4.15x3+0.5x4+x5+1.8x6–x7–x8|. Ограничения: -10£ xi £10, i=1,8 Минимум: F(х*)= -1. 4. Функция n переменных (в данном исследовании N = 10):
Ограничения: 0£ xi £10, i=1,N. Минимум: F(х*)=0, для которой U=0, xi=xi*, i=1,N. 5. Функция Растригина n=10: F(х1…х10)=S(10cos(2pxi)- xi2)-100 Ограничения: -5.12£xi£5.12, i=1,2…10. Максимум: Ф(х*)=0. Среди тестовых функций такие, которые имеют как один локальный экстремум (F1–F2), так и сложные многоэкстремальные функции высокой размерности (F3, F4, F5), имеющие и локальные, и глобальные экстремумы и практически не решаемые классическими методами оптимизации. Для исследования использовались следующие параметры: · размер популяции – 50 хромосом; · вероятность кроссинговера – 100 %; · количество запусков алгоритма – 500. Для подтверждения эффективности найденных параметров ГА и анализа данных использовались методы математической статистики. Результаты экспериментов с исследуемыми методами оценивались путем расчета математического ожидания, дисперсии и построения доверительного интервала, который накрывает оцениваемый параметр с известной степенью достоверности.
где Доверительный интервал может быть рассчитан по формуле:
где tna/2 – коэффициент распределения Стьюдента. Были получены параметры, приведенные в таблице 1 [2]: Таблица 1
С найденными параметрами было произведено 500 запусков для каждой функции и построены доверительные интервалы с использованием двухэтапной оптимизации (табл. 2). Таблица 2
Однако проведение таких исследований очень трудоемко и не решает проблему подбора параметров под произвольную задачу. Для правильного выбора параметров необходимо знать поведение функции на всей области определения. В реальных задачах знать заранее тип функции практически невозможно. Для решения этой задачи был разработан конструктор ГА. Его задача состоит в подборе 7 основных параметров для выбранной функции. Принцип действия конструктора следующий: · пользователь выбирает параметры ГА, которые конструктор будет искать, и накладывает необходимые ограничения на эти параметры. Количество параметров определяет количество генов хромосом конструктора; · происходит запуск конструктора: формируется популяция, причем хромосомами являются параметры ГА; · для вычисления функции пригодности для каждой хромосомы производится запуск ГА (вложенный ГА) с теми параметрами, которые хранятся в хромосоме на выбранной пользователем функции. Значением функции пригодности хромосомы конструктора ГА будет являться лучшее значение функции пригодности, полученное вложенным ГА на основе параметров из данной хромосомы; · следующие этапы соответствуют этапам работы обычного ГА. В результате действия конструктора ГА пользователь получает параметры, наиболее эффективные при оптимизации исследуемой функции. Тесты, проведенные с конструктором ГА, доказали его эффективность. Подтверждение работоспособности предложенных методик проводилось путем решения практической задачи – организации управления запасами и оптимизации раскроя ленточного материала в условиях случайного поступления заказов. Выбор данной задачи не случаен: отсутствие в текущий момент алгоритмов и методы ее решения обусловленны NP-сложностью задачи и большой размерностью. Практическая ценность задачи приводит к постоянным исследованиям в данной области. Рассмотрим машиностроительное предприятие, выпускающее k различных типов комбайнов. При производстве комбайнов используются m заготовок прямоугольной формы Mz=(wz, dz), z=1..m, где wz, dz – соответственно ширина и длина заготовки. Для удобства расчета примем, что wz£dz, следовательно, wzÎ(0, h]. Множество всех заготовок обозначим через M. Для производства каждого комбайна необходимо некоторое множество Zi, i=1..k заготовок, причем ZiÍM, i=1..k и в общем случае Zi Ç Zj ≠Æ, i,j=1..k. Получение заготовок происходит путем вырубания их из полубесконечной полосы заданной ширины h и неограниченной длины. Введем прямоугольную систему координат: оси OX и OY совпадают со сторонами полосы, причем OX направлена вдоль неограниченной грани полосы. Положение z-й заготовки назовем горизонтальным, если ее сторона dz параллельна неограниченной грани полосы, а вторая сторона перпендикулярна ей. В противном случае положение назовем вертикальным. Заготовки могут находиться только в горизонтальном или вертикальном положении. Положение каждой заготовки z зададим вектором (xz, yz). Всего за смену возможно обработать полосу длиной Lmax. Перед вырубанием заготовок их укладывают на полосу по определенному алгоритму, после чего происходит отрубание части полосы длины l, где l=lmin .. lmax, lmin³0; lmax>0; lmin £ lmax, wz£ lmax, dz£ lmax, z=1..m. Обозначим через rb получившийся раскрой, через lrb его длину, а через nzb обозначим количество заготовок типа z=1..m, которые находятся в раскрое, где b= 1.. bmax, bmax – количество отрезов в течение дня. Через rbопт обозначим оптимальный раскрой, который возможен для rb упаковки, а через lrbопт – ее длину. После каждого отреза меняется состав и количество заготовок, поэтому rbопт зависит от b. Через lrb’ обозначим верхнюю оценку раскроя b, полученную аналитически. График заказов комбайнов имеет вид: Q(i, d, ni, Сштр.), где i=1..k – тип комбайна, d – дата заказа, ni>0 – количество комбайнов типа i, которое необходимо произвести к дате заказа, Cштр. – штраф за невыполнение заказа. Cштр.= Сштр.д.∙ ∆T+ + Cштр.ф., где Сштр.д.– штраф за один день просрочки; ∆T – количество дней просрочки выполнения заказа; Cштр.ф – фиксированная часть суммы штрафа; Сштр.д. ³ 0; Cштр.ф. ³ 0. Через Pz, z = 1..m обозначим остаток заготовок типа z на складе на начало расчета, а Cхр.z, z = 1..m – стоимость хранения единицы заготовки типа z на складе в течение одного дня. Площадь склада, то есть максимальная площадь всех заготовок, которые могут находиться на складе одновремен- но, – Sскл. Sскл. ³ ∑Pz∙wz∙dz, z = 1..m для любого момента расчета; Сштр.s. – штраф за превышение вместимости склада за единицу площади. При расчете примем, что заготовки поступают в производство на следующий день после вырубки, а на склад – в тот же день. Предлагаемый алгоритм можно сформулировать следующим образом: 1) на основе заданных справочников заготовок, комбайнов и графика производства комбанов формируется массив всех деталей, которые необходимо изготовить с указанием типа заготовки (z = 1..m), даты и количества заготовок; 2) на основе этих данных запускается ГА, решающий задачу раскроя. В качестве генов выступают индексы заготовок z = 1..m; 3) задача управления запасами решается через вычисления функции пригодности. Функция пригодности ГА зависит от следующих параметров: · F% – процент заполнения данной хромосомы (F% -> max); · Sхр – затраты на хранение заготовок, уложенные в данной хромосоме (Sхр ® min); · Кост – коэффициент, учитывающий вероятность выполнения плана изготовления всех заготовок в срок (Кост ® max). Для вычисления Кост используются следующие параметры: - nmax z – максимальное количество заготовок z-го типа, которое может быть уложено на один метр полотна; - Nмz – оставшееся количество метров полотна, которое планируется вырубить, до даты готовности заготовок; - Nост z – осталось вырубить заготовок данного типа. Кост i ~ (nmax z * Nм z) / Nост z; Кост ~ Кост z. Точные формулы определены эмпирически. Fitn = F(F%, Sхр, Кост), Fitn ® max. Полученные результаты доказали работоспособность предложенного алгоритма. Разработанная инструментальная среда позволяет значительно ускорить процесс подбора параметров ГА под решаемую задачу, а также оценить эффективность найденных решений за счет расчета основных статистических данных полученных результатов. Результаты проведенного исследования используются при решении задачи управления запасами и ленточного раскроя. Список литературы 1. Комарцова Л.Г. Двухэтапный алгоритм обучения нейронной сети на основе генетического поиска // Нейрокомпьютеры. Разработка и применение.-М.: Радиотехника. -2001. -№1. 2. Комарцова Л.Г., Голубин А.В. Исследование свойств генетических алгоритмов оптимизации //Методы исследования и проектирования сложных технических систем: Сб. статей. -М.: Изд-во МГТУ им. Н.Э. Баумана. - 2001 (Тр. МГТУ №580). 3. Комарцова Л.Г., Голубин А.В. Использование Конструктора для определения параметров генетического алгоритма // Тр. V Междунар. симпоз.: Интеллектуальные системы (INTELS'2002). -М.:МГТУ им. Н.Э. Баумана.-2002. 4. Курейчик В.М. Генетические алгоритмы. Состояние. Проблемы. Перспективы // Изв. РАН. Теория и системы управления. -1999. - №1. 5. Practical Handbook of Genetic Algorithms// Ed. By I. Chambers. -Washington. USA, CRC Press, 1999. 6. Tongchim S., Chongstitvatana P. Parallel genetic algorithm with parameter adaptation // In Proceedings of IEEE International Conference on Evolutionary Computation, 1999. | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=522 |
Версия для печати Выпуск в формате PDF (0.95Мб) |
| Статья опубликована в выпуске журнала № 3 за 2005 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Формулировка задачи планирования линейных и циклических участков кода
- Информационная система оптимизации расписания доставки грузов от производителей сырья
- Автоматизированное рабочее место расчета стоимости эксплуатации кораблей
- Общее информационное пространство задач кораблестроения. Концепция построения информационной модели
- Время перемещать камни
Назад, к списку статей



 ,
, ,
,  .
.
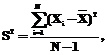
 – математическое ожидание; S – дисперсия; N – число независимых наблюдений.
– математическое ожидание; S – дисперсия; N – число независимых наблюдений.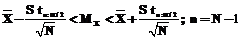 ,
,