Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Программный модуль для расчета аппроксимирующих полиномов по методу наименьших квадратов
Аннотация:
Abstract:
| Автор: Джагаров Ю.А. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 11451 |
Версия для печати Выпуск в формате PDF (0.95Мб) |
Эмпирическую функцию Y=f(X)={Xi, Yi}, i=1,2, … n (1) удобно аппроксимировать полиномами вида
или
k≠0 – степень полинома. Заменой переменной z=x–1 полином вида (3) приводится к виду (2). Расчет коэффициентов ai по методу наименьших квадратов производится исходя из условия минимальности функционала
которое приводит к системе нормальных уравнений вида [1]:
Система (5) сводится к системе линейных уравнений, для чего в средах типа Excel, MathCad и т.п. необходимо выполнить вручную значительный объем операций. Однако методом индукции можно показать, что система (5) приводится к системе линейных относительно ai уравнений вида:
из которой для матрицы системы M и вектора B свободных членов получаем следующие формализации:
Здесь j – номер строки, i – номер столбца. Вид системы (6) определяется количеством данных n, элементами xi и yi функции (1) и степенью k аппроксимирующего полинома. Формализации (7) и (8) позволяют построить программный модуль, представленный на фигурах 1–3 (QBASIC 4.5), автоматически формирующий матрицу М и вектор В по заданной функции (1) и степени полинома k, и вычисляющий коэффициенты ao,a1,…,ak аппроксимирующих полиномов (2) и (3).
В строке Sp (фиг. 2) выполняется ввод стартового значения числа k. При вводе k=0 считается, что k=1. При k<0 массив X0(n) анализируется на наличие нулевых элементов. При их обнаружении выдается сообщение о невозможности расчета, поскольку переменная z в этом случае не существует, и управление передается на строку 5. В противном случае массив X(n) принимает значения, обратные соответствующим значениям массива X0(n). При k>0 массивы X(n) и X0(n) тождественны. В строке 20 формируются массивы m (k+1,k+1), B(k+1) и a(k+1), предназначенные соответственно для формирования матрицы (7), вектора (8) и коэффициентов ai полиномов (2) и (3). В строках 20÷30 выполняется вычисление матрицы (7) и вектора (8), по которым в блоке B (фиг. 2) выполняется расчет коэффициентов ai, являющихся корнями системы (6). В блоке В решения системы линейных уравнений используется метод Гаусса [3]. В строках V1÷D1 (фиг. 1) выполняется расчет функционала (4) для введенной функции (1) и выбранного значения k. Здесь же выполняется вывод на экран значений ai, S, n, k, значения ε, равного разности двух последовательных значений S и минимального значения Smin, полученного в текущем сеансе работы. В нижних строках экрана содержится подсказка о клавишах управления. Для перехода к большему на единицу значению k следует нажать клавишу “↑”, к значению на единицу меньшему, чем текущее, – клавишу “↓”. Для ввода нового .стартового значения k нужно нажать клавишу “←”. Для ввода новой функции (1) или завершения сеанса работы нужно нажать клавишу “Esc”. Для вывода на принтер результата отчета нужно нажать клавишу “→”, при этом управление передается блоку C (фиг. 2). Текст отчета выводится на экран и, после нажатия клавиши “Y”, на принтер. Нажатие любой иной клавиши возвращает в режим расчета. 5 COLOR 14, 9 ON ERROR GOTO Er: q$ = ") = 0 - is inadmissible value" d5: CLS : INPUT "Input number of data n, for End input n = 0 "; n: CLS IF n = 0 THEN END ELSEIF n < 0 THEN BEEP: GOTO d5 END IF REDIM X0(n), x(n), y(n): p = 0 GOSUB a ' To the modul of enter the data Sp: FOR i = 1 TO n: x(i) = X0(i): NEXT i INPUT "Input power of polinom"; L: CLS : S0 = 0 10 IF L = 0 THEN k = 1 ELSEIF L < 0 THEN k = -L: FOR i = 1 TO n IF x(i) = 0 THEN PRINT "X("; i; q$: BEEP: SLEEP (4): GOTO 5 x(i) = 1 / X0(i): NEXT i ELSEIF L > 0 THEN k = L END IF CLS : LOCATE 11, 31: PRINT "Please wait !" 20 REDIM m(k + 1, k + 1), B(k + 1), a(k + 1) FOR j = 1 TO k + 1: B = 0: FOR r = 1 TO n B = B + y(r) * x(r) ^ (j - 1): NEXT r: B(j) = B FOR i = 1 TO k + 1: S = 0: FOR r = 1 TO n S = S + x(r) ^ (j + i - 2): NEXT r: m(j, i) = S 30 NEXT i, j: GOSUB B: V1: S = 0: FOR r = 1 TO n: Pl = 0 FOR i = 1 TO m: Pl = Pl + a(i) * x(r) ^ (i - 1) NEXT i: S = S + (Pl - y(r)) ^ 2: NEXT r: CLS IF p = 0 THEN Eps = S: Smin = S ELSE Eps = S0 - S IF L = 0 THEN V = 1 ELSE V = L IF Smin >= S THEN Smin = S: f = L PRINT "n="; n; " S="; S; " Epsilon="; Eps; PRINT " Power of polinom ="; V: S0 = S PRINT "Smin="; Smin; " for power of polinom ="; f: PRINT PRINT "Coefficients of polinom of power = "; V; ":" FOR i = 1 TO m IF i = 46 OR i = 92 THEN PRINT "Press any key to continue": G$ = INPUT$(1) PRINT "A("; i - 1; ")="; a(i), NEXT i: PRINT : p = p + 1: SLEEP (10) PRINT " To forwad press "; CHR$(24), , " To back press "; CHR$(25) PRINT " To new pawer of polynom press "; CHR$(17), PRINT " To result and printing press "; CHR$(16) PRINT " To new data or End press Esc"; PRINT TAB(39); "To show the first lines press Ctrl+"; CHR$(17): x$ = "" Dl: DO WHILE x$ = "": x$ = INKEY$: LOOP IF x$ = CHR$(0) + CHR$(72) THEN L = L + 1: x$ = "": CLS : GOTO 10 ' Pointer up - to the forward ELSEIF x$ = CHR$(0) + CHR$(80) THEN L = L - 1: x$ = "": CLS : GOTO 10 ' Pointer down - to the back ELSEIF x$ = CHR$(0) + CHR$(75) THEN x$ = "": CLS : GOTO Sp 'Pointer to the left - to the new power of poiyno Фигура 1 ELSEIF x$ = CHR$(27) THEN CLS : x$ = "": CLS : GOTO 5 'Esc - to the new data or End ELSEIF x$ = CHR$(0) + CHR$(77) THEN x$ = "": CLS : GOSUB C 'Pointer to the right - to printing of the result ELSEIF x$ = CHR$(0) + CHR$(115) THEN x$ = "": LOCATE 1, 1: PRINT "n="; n; " S="; S; " Epsilon="; Eps; PRINT " Power of polinom ="; V PRINT "Smin="; Smin; " for power of polinom ="; f: GOTO Dl END IF x$ = "": BEEP: GOTO Dl END B: 'Colculation of roots of system linear equations by Gauss [3] m = k + 1 FOR i = 1 TO m - 1: FOR j = i + 1 TO m m(j, i) = -m(j, i) / m(i, i): FOR r = i + 1 TO m m(j, r) = m(j, r) + m(j, i) * m(i, r): NEXT r B(j) = B(j) + m(j, i) * B(i): NEXT j: NEXT i a(m) = B(m) / m(m, m) FOR i = m - 1 TO 1 STEP -1: h = B(i) FOR j = i + 1 TO m: h = h - a(j) * m(i, j): NEXT j a(i) = h / m(i, i): NEXT i RETURN Er: CLS IF ERR = 6 OR ERR = 7 OR ERR = 11 THEN GOTO Er1 ELSE ON ERROR GOTO 0 Er1: PRINT "Resource of computer is not enough fop power = "; L BEEP: SLEEP (2) IF L >= 0 THEN L = L - 1 ELSE L = L + 1 RESUME 10 C: PRINT TAB(27); " RESULT OF SEARCH": PRINT PRINT "n="; n; " S="; S; PRINT " Power of polinom ="; V PRINT "Smin="; Smin; "for power of polinom = "; f: PRINT PRINT "Coefficients of polinom of power ="; V; ":" FOR i = 1 TO m IF i = 46 OR i = 92 THEN PRINT "Press any key to continue": G$ = INPUT$(1) PRINT "A("; i - 1; ")="; a(i), NEXT i: PRINT PRINT "For printing press Y else press any key for return to the back" G$ = INPUT$(1) IF G$ = "Y" OR G$ = "y" THEN GOTO r ELSE GOTO r1 r: 'LPRINT TAB(27); " RESULT OF SEARCH": PRINT 'LPRINT "n="; n; " S="; S; 'LPRINT " Power of polinom ="; V 'LPRINT "Smin="; Smin; "for power of polinom = "; f: PRINT 'LPRINT "Coefficients of polinom of power ="; V; ":" 'FOR i = 1 TO m: LPRINT "A("; i - 1; ")="; a(i), 'NEXT i BEEP r1: RETURN V1 Фигура 2 Таким образом, программный модуль позволяет, последовательно начиная с произвольного стартового значения k, просматривать результаты расчета аппроксимирующих полиномов для произвольного k, значение которого можно произвольно изменять в ходе работы. a: ne = 1 Mi5: FOR i = ne TO n IF i <= ne THEN i = ne PRINT "Input X("; i; "); Y("; i; ")" INPUT "X"; x$: IF x$ = "e" OR x$ = "E " THEN PRINT : GOTO Mi11 IF x$ = "=" THEN PRINT "Keep X"; i; "="; X0(i); "Y"; i; "="; y(i): GOTO Mi10 ELSEIF x$ <= "*" OR x$ >= ">" THEN i = i - 2: PRINT : GOTO Mi10 END IF INPUT "Y"; y$ X0(i) = VAL(x$): y(i) = VAL(y$) PRINT " Accepted X="; X0(i); " Y="; y(i) Mi10: NEXT i Mi11: CLS : PRINT "The input is over" PRINT "If need correction" PRINT "input ", else any key" Mi15: d$ = INKEY$: IF d$ = "" THEN GOTO Mi15 IF d$ = "y" OR d$ = "Y" THEN GOTO Mi16 ELSE GOTO Mi18 Mi16: CLS : PRINT "Starting-element X0("; ne; ");Y("; ne; ")" PRINT "If need correction " PRINT "input ", else any key" Mi17: d$ = INKEY$: IF d$ = "" THEN GOTO Mi17 IF d$ = "y" OR d$ = "Y" GOTO Mi2 ELSE i = n: GOTO Mi5 Mi2: INPUT "The number of Starting-element"; ne: IF ne = 0 THEN GOTO Mi2 IF ne > n THEN GOTO Mi2 GOTO Mi5 Mi18: CLS : RETURN Фигура 3 При больших значениях k, определяемых мощностью компьютера, возможны ошибки переполнения, деления на машинные нули и т.п. Для предотвращения авоста в этих случаях управление передается блоку Er (фиг. 2), выдающему соответствующее сообщение, изменяющему значение k на единицу и передающему управление на строку 10, что позволяет продолжить расчет в обратном направлении. Обработка нажатий клавиш выполнена на основе синтеза кодов [4]. Список литературы 1. Линник О.В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. - М.: Наука, 1982. – 240 с. 2. Джагаров Ю.А. Программный блок ввода с коррекцией // Программные продукты и системы.-1999.- № 3. 3. Дьяконов В.П. Справочник по алгоритмам и программам на языке бейсик для персональных ЭВМ. - М.: Наука, 1987. – 240 с. 4. Джагаров Ю.А. Отслеживание нажатий клавиш клавиатуры на основе синтеза кодов //Программные продукты и системы.- 2000.- №1. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=524 |
Версия для печати Выпуск в формате PDF (0.95Мб) |
| Статья опубликована в выпуске журнала № 3 за 2005 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Место XML-технологий в среде современных информационных технологий
- Компьютерные технологии сегодня: тенденции и прогнозы
- Системное тестирование программных изделий
- Статическая обработка спецификаций программных систем реального времени
- Параллельная обработка в алгоритмах визуализации с трассировкой лучей
Назад, к списку статей



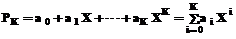 (2)
(2) , (3)
, (3)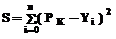 , (4)
, (4)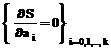 . (5)
. (5)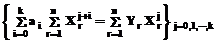 , (6)
, (6)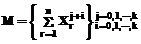 , (7)
, (7)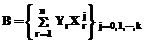 . (8)
. (8) В строке d5 (фиг. 1) выполняется ввод и анализ числа n. Значение n=0 является признаком окончания сеанса работы. При n≠0 формируются массивы X0(n), Y(n), содержащие заданную функцию (1) и вспомогательный массив X(n). Функция (1) вводится через клавиатуру с помощью блока ввода, строки a÷Mi2 (фиг. 3), построенного на основе внешнего управления параметром цикла [2], что позволяет корректировать введенные дан- ные как в процессе ввода, так и после его завершения.
В строке d5 (фиг. 1) выполняется ввод и анализ числа n. Значение n=0 является признаком окончания сеанса работы. При n≠0 формируются массивы X0(n), Y(n), содержащие заданную функцию (1) и вспомогательный массив X(n). Функция (1) вводится через клавиатуру с помощью блока ввода, строки a÷Mi2 (фиг. 3), построенного на основе внешнего управления параметром цикла [2], что позволяет корректировать введенные дан- ные как в процессе ввода, так и после его завершения.