Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Программная система согласованной оптимизации бюджетных целевых программ
Аннотация:
Abstract:
| Авторы: Семенов Н.А. (dmitrievtstu@mail.ru) - Тверской государственный технический университет (профессор кафедры «Информационные системы»), г. Тверь, Россия, доктор технических наук, Кузнецов В.Н. (is@tstu.tver.ru) - Тверской государственный технический университет, г. Тверь, Россия, доктор технических наук, Цибарев М.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 9818 |
Версия для печати Выпуск в формате PDF (1.97Мб) |
Разработка программной системы согласованной оптимизации бюджетных целевых программ осуществлена на основе метода согласованной оптимизации в нечетких системах [1]. Система предназначена для поддержки программного составления областного бюджета на основе практической оптимизации (анализируются не менее двух вариантов бюджетных целевых программ) и согласования интересов и целей органов исполнительной власти, исполнителей бюджетных целевых программ и населения на примере Тверской области. Программная система разработана с применением средств Delphi и базы данных Oracle и включает модули поддержки системного анализа целей и задач бюджетных целевых программ, поддержки формирования вариантов постановок задач согласованной оптимизации, их решения и послеоптимизационного анализа, поддержки анализа вариантов бюджетных целевых программ, поддержки их презентации и процессуального консультирования по согласованной оптимизации и формированию бюджетных целевых программ. Программная система осуществляет поддержку следующих процедур. 1. Построение трехуровневой структуры целей и факторов (третий уровень) влияния, включая мероприятия по развитию и реструктуризации объекта программы. 1.1. Определение перечня и содержания целей первого и второго уровней и факторов влияния третьего уровня. 1.2. Определение базового, прогнозируемого и планируемых периодов (по годам). 1.3. Определение для каждой i=1,2,…,n цели второго уровня описывающих их показателей kij, j=1,2,…,m использования бюджетной целевой программы. 1.4. Построение качественной шкалы разностей или количественной шкалы отношений для измерения приращений ∆kij показателей целей последующего периода относительно предыдущего с применением лингвистических координат или нормированных значений показателей ∆kij = (kijt - - kij(t-1),)/ kijt, 0 ≤ ∆kij ≤ 1. 1.5. Описание функциональной зависимости индикатора достижения цели ∆wo(t) бюджетной целевой программы от индикаторов достижения целей второго уровня ∆wij(t), приращений их показателей ∆kij(t), увеличения объемов финансирования ∆si(t) на реструктуризацию по целям второго уровня. ∆wo(t) ≈ ∆wi (t) ≈ Dkij (t) ≈ ∆wo(t)≈ При этом считается, что существует зависимость оценки достижения цели wо(t) от оценок достижения целей второго уровня wi(t), их показателей kij(t), объемов финансирования si(t) на ре- структуризацию по целям второго уровня wo = = W ( w ( k ( s ) ) ), w = (w1,w2 ,…, wi,…,wn), k = = (k1,k2,…, kij,…,knm), s = (s1, s2,…, si,…, sn), ∆wo(t)= wo(t) - wo(t - 1), ∆wi( t)= wi(t) – wi(t - 1), ∆kij(t) = kij(t) - kij(t – 1), ∆si(t) = si(t) - si(t - 1). Также считается, что существуют производные ¶wo /¶wi , ¶wi /¶kij , ¶kij /¶si, с помощью экспертных оценок которых в виде весовых коэффициентов по правилу полного дифференциала определяются приращения функций по приращениям аргументов. 2. Расчет индикаторов достижения целей бюджетной целевой программы для прогнозируемого года относительно базового. 2.1. Сбор данных по показателям, описывающих цели разных уровней и факторы влияния бюджетной целевой программы для базового и прогнозируемого года. Для прогнозируемого года определяются с упреждением три варианта данных для пессимистической (вероятность риска р=0,3), для наиболее вероятной (вероятность риска р=0,5), для оптимистической ситуации во внутренней и внешней средах. 2.2. Определение экспертами коэффициентов веса по значимости целей второго уровня относительно общей цели и коэффициентов веса показателей по значимости относительно соответствующих целей второго уровня. Для прогнозируемого года определяются с упреждением три варианта. 2.3. Определение экспертами лингвистических оценок разностей качественных и количественных показателей целей или расчет количественных нормированных значений приращений показателей целей второго уровня. Для прогнозируемого года определяются с упреждением три варианта. 2.4. Расчет индикаторов достижения целей бюджетной целевой программы. Для прогнозируемого года определяются с упреждением три варианта, среднее значение и среднее квадратичное индикаторов достижения целей и использования земли. Среднее квадратичное применяется для оценки риска при упреждении. 3. Многошаговый итерационный процесс оценки и выбора управленческих решений по реализации бюджетной целевой программы. 3.1. Начало процесса. 3.2. Построение дерева решений, учитывающего два этапа решений по реструктуризации и два этапа стратегий природы по выбору пессимистической (вероятность риска р=0,3), наиболее вероятной (вероятность риска р=0,5) и оптимистической ситуации во внутренней и внешней средах. 3.3. Определение экспертами трех вариантов коэффициентов веса ¶wo /¶wi , ¶wi /¶kij по значимости целей второго уровня относительно общей цели и коэффициентов веса показателей по значимости относительно соответствующих целей второго уровня. 3.4. Определение экспертами трех вариантов коэффициентов веса ¶w /¶wо(t) по значимости цели бюджетной целевой программы на всем прогнозируемом периоде t Î T относительно цели на конкретных периодах времени t. 3.5. Определение экспертами или системными аналитиками трех вариантов коэффициентов веса ¶kij/¶si по значимости влияния дополнительного финансирования на приращения показателей второго уровня и ограничений по финансированию решений по реструктуризации сi(t) и со = 3.6. Расчет и послеоптимизационный анализ трех вариантов, соответствующих дереву решений, оптимальной задачи по расчету оптимального дополнительного финансирования решений по реструктуризации ∆w ≈ ´ (¶wi /¶kij )(t) ´ (¶kij /¶si )(t) ´ Dsi (t) ® max, ∆si(t) £ сi(t) и ∆so(t) = å ∆si(t) £ со = å сi(t). 3.7. Выбор лучшего варианта дополнительного финансирования по критерию максимума среднего выигрыша и анализ риска по среднему квадратичному индикатора использования бюджетной целевой программы. 3.8. Формирование факторов влияния на цели второго уровня, то есть плана мероприятий и дополнительного их финансирования по годам и целям второго уровня. Проверка обеспеченности финансирования. Если не обеспечено, переход к 3.5. 3.9. Детализация показателей целей второго уровня для уточнения системными аналитиками экспертных оценок весовых коэффициентов по 3.3 – 3.5. 3.10. Остановка процесса или переход к 3.1. Рассмотрим в качестве контрольного примера согласованную оптимизацию бюджетной целевой программы (2003-2005) по развитию и реструктуризации имущественно-земельного комплекса Тверского региона. На каждом шаге процесса осуществляется оптимизация финансирования работ по индикатору использования земли и развития имущественно-земельного комплекса региона. В итерационном процессе решается нелинейная задача выпуклой оптимизации с применением градиентных методов [2]. На каждом шаге определяется оценка градиента целевой функции с применением весовых коэффициентов. Так как градиентные методы являются устойчивыми к точности оценки градиента, то экспертные оценки могут быть применимы для решения этой задачи. Это обеспечивает достаточную скорость сходимости к оптимальному решению на первых шагах. Процесс оптимизации представлен в виде дерева решений (осуществляется два этапа принятия решений), которому соответствуют решение о состоянии в 2003 году и решение о финансировании на 2004 и 2005 годы и два этапа выбора состояний природы (внутренней и внешней среды в 2003 году и в 2004 и 2005 годах). В процессе оптимизации применяется критерий максимума среднего риска для учета риска в 2004 и 2005 годах и решается три варианта задач оптимизации финансирования на 2004 и 2005 годы. Задача согласованной оптимизации в соответствии с [1] будет иметь вид: ∆w ≈ ×(¶wo /¶wi)(t) ´ (¶wi /¶si )(t) ´Dsi (t) ® max, ∆si(t) £ сi(t) и ∆so(t)= å ∆si(t) £ со = å сi(t) или ∆w ≈ ´ (¶kij /¶si )(t) ´ Dsi (t) ® max, ∆si(t) £ сi(t) и ∆so(t)= I = { i êi=1,2,…,7 }, J = { j êj = 1,2,…,mi }, R = { r êr = 1,2,3 }. После решения трех вариантов задач согласованной оптимизации финансирования для трех вариантов прогнозов о состоянии на 2003 год выбирается наилучший по наибольшему значению индикатора использования земли имущественно-земельного комплекса Тверской области для периода 2003–2005 годов. Это и является решением для наиболее вероятного прогноза. Список литературы 1. Кузнецов В.Н., Семенов Н.А. Нечеткие экономические информационные системы и их применение в поддержке принятия согласованных решений // Интегрированные модели и мягкие вычисления в искусственном интеллекте. / Сб. тр. 2 Междунар. науч.-прак. сем. - М.: Физматгиз, 2003. - С.380-385. 2. Джоффрион А., Дайер Дж., Файнберг А. Решение задач оптимизации при многих критериях на основе человеко-машинных процедур. – В кн.: Вопросы анализа и процедуры принятия решений. - М.: Мир, 1976. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=533 |
Версия для печати Выпуск в формате PDF (1.97Мб) |
| Статья опубликована в выпуске журнала № 2 за 2005 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Интеллектуальная поддержка реинжиниринга конфигураций производственных систем
- Эвристические и точные методы программной конвейеризации циклов
- Оптимизация обработки информационных запросов в СУБД
- Механизм контроля качества программного обеспечения оптико-электронных систем контроля
- Автоматизированная информационная система маркетолога
Назад, к списку статей



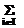 (¶wo /¶wi)(t) ´ Dwi(t);
(¶wo /¶wi)(t) ´ Dwi(t);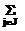 (¶wi /¶kij )(t) ´ Dkij (t);
(¶wi /¶kij )(t) ´ Dkij (t); å сi(t).
å сi(t).