Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Об оптимизации информационной структуры летательного аппарата как средстве снижения затрат на контроль технического состояния
Аннотация:
Abstract:
| Авторы: Бизяев Р.В. () - , Давыдов О.И. () - , Калинин С.Ю. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 10157 |
Версия для печати Выпуск в формате PDF (1.31Мб) |
В условиях тенденции к усложнению бортовых систем (БС) летательных аппаратов (ЛА), сопровождающейся ростом числа контролируемых параметров (КП), целесообразным является построение моделей и разработка методов контроля технического состояния (ТС) БС на основе обобщенных параметров. При этом важным является вопрос формирования обобщенных параметров (ОП), поскольку потеря информации о значениях первичных контролируемых параметров снижает достоверность контроля и влечет несвоевременное принятие мер по его результатам. Множество состояний БС ЛА характеризуется множеством признаков, элементы которых суть значения КП: Х0={Х01, Х02,...,Х0|Х0|}, (1) ХП={ХП1, ХП2,...,ХП|ХП|}, (2) где Х0 – множество значений определяющих параметров БС в целом; ХП – множество значений определяющих параметров П-й подсистемы БС, П=1·К; К – число подсистем сложной системы. Соответствие множеств признаков множествам состояний устанавливается посредством функций соответствия, зависящих от способа контроля параметров, структуры БС, принятых допущений. В совокупности (1), (2) задают параметрическую модель, являющуюся основой для построения других моделей БС. В [1] разработана матричная (табличная) модель БС на основе разбиения (1), (2) на непересекающиеся в каждом разбиении подмножества:
где I(.) – количество элементов в подмножестве (.)-го множества. Приведенные разбиения дополним условиями: Аоgо ∩ Атоdо=Хоgо d0, (7) Апg1 ∩ Атпd1=Хпg1 d1 , где g0, g1, d0, d1 – те же, что и в (3)-(6). Последние означают, что разбиения сформировали матрицы из значений контролируемых параметров, строки и столбцы которой суть значений контролируемых параметров БС ЛА. При допусковом контроле параметров значению каждого параметра ставится в соответствие логическая переменная в соответствии с условием: хή= где ή=1...N, N – общее число КП БС, определяемое на основании (1) и (2) следующим образом:
На значениях логических переменных наборов подмножеств (3)-(6) сформируем конъюнкции следующим образом:
Совокупность подмножеств (3)-(6) с заданным на нем отношением порядка, фиксирующим место каждого КП с его значением и конъюнкцией (8)-(11), задает матричную модель контроля БС ЛА. Конъюнкции (8)-(11) представляют собой ОП БС в целом и ее подсистем. По ОП (8) определяется ТС БС в целом с глубиной, задаваемой одним ОП. Так, нулевое значение любой конъюнкции из (8) свидетельствует о выходе значения одного или нескольких КП из набора, формирующего конъюнкцию, за пределы поля допуска (полей допуска), что позволяет определить ТС БС в целом как неработоспособное. Дополнительная проверка ОП (10) позволяет благодаря условиям (7) найти ОП с нулевым значением из (3) и (4), а тем самым и подсистему БС, в которой появился дефект. Иначе говоря, только по ОП можно проводить контроль работоспособности и поиск дефекта в БС с глубиной до подсистемы БС, КП которой введены в (1). Аналогично по ОП (9), (11) можно определить ТС подсистемы БС с глубиной до элемента ее структуры, КП которой введе- ны в (2). Таким образом, только по ОП можно осуществлять проверку работоспособности и поиск дефекта в БС с глубиной, определяемой уровнем структуры БС, представленным КП в (1), (2). Общее число ОП равно: Минимизация числа ОП, проведенная на основе геометрического программирования [2], позволила получить следующие соотношения, аналогичные для L0(m0,n0) и Ln(mn,nn) и поэтому неиндексированные: m*= L*= Снижение затрат на контроль БС по ОП обусловливается минимизацией их числа при заданном количестве КП и снижением длины линий связи источников информации с устройством обработки информации. Количественно эти снижения оцениваются на основании показателей:
где l1 – средняя длина линии связи от формирователя обобщенных параметров БС в целом до устройства обработки информации (УОИ); l1п – средняя длина линии связи от формирователя обобщенных параметров п-й подсистемы БС до УОИ. Анализ показателей (13)-(15) позволяет сделать вывод о влиянии на них структуры БС, причем увеличение степени интеграции БС как объекта контроля приводит к росту значений показателей. Последнее позволяет сделать вывод о целесообразности построения матричной модели не БС, а структуры бортового оборудования, расположенного в определенном месте на борту ЛА. При этом в состав контролируемой структуры могут входить структурные элементы различных БС. Решение задачи минимизации средних затрат на контроль ТС по ОП предполагает наличие следующих исходных данных: 1) физических моделей БС ЛА; 2) перечня КП БС – X1,...,XN с выделенным ОП – X0 и параметрами хп, п=1...к для каждой БС; 3) перечня аварийных параметров Xoa для БС и ЛА в целом; 4) топографии ЛА с предполагаемым размещением бортовой аппаратуры; 5) математического ожидания и дисперсии времени на проверку одного КП – 6) математического ожидания затрат в еди- ницу времени того или иного вида ресурса на кон- троль – С. В качестве ограничений введены следующие: - длина линий связи системы контроля – - минимальное время развития дефекта в аварийную ситуацию по каждому аварийному определяющему параметру – tas, S = 1….T. Формальная постановка задачи имеет вид: найти
при ограничениях Так как величины найти
при ограничениях
В отличие от традиционных постановок задач минимизации средних затрат на контроль последние сводятся к оптимальному с точки зрения (17) разбиению контролируемой структуры бортового оборудования ЛА. Введем определение: информационная структура объекта контроля – совокупность источников информации с формирователями ОП, линиями связи, размещенных на объекте в определенных местах. Таким образом, задача (17) является задачей синтеза оптимальной информационной структуры ЛА и может быть решена методом последовательных приближений. Сущность метода заключается в декомпозиции информационной структуры ЛА, полагая ее в первом приближении интегрированной в «монолит» с последующим снижением степени интегрирования на каждом шаге декомпозиции (приближения) с учетом (18), (19). Алгоритм, реализующий метод последовательных приближений, включает следующие шаги. 1. На основании топографии ЛА выбрать вариант его информационной структуры с максимально возможной степенью интеграции структурных элементов различных БС. 2. Проверить наличие в перечне КП множества Хоа аварийных ОП, при отсутствии Хоа перейти к шагу 5, в противном случае – к шагу 3. 3. Сформировать первый уровень, матричной модели контроля ЛА из Хоа. Вычисление Lоа произвести по формулам (12). 4. Проверить выполнение условия (18). При отрицательном результате перейти к шагу 9, в противном случае – к следующему шагу. 5. Сформировать второй уровень матричной модели контроля ЛА из Хо. Вычисление Lо произвести по формулам (12). 6. Проверить в перечне КП наличие множеств Хп, п=1...к, при отсутствии множеств перейти к шагу 8, в противном случае – к следующему шагу. 7. Сформировать третий уровень матричной модели контроля ЛА из КП Хп. Вычисление Lп произвести по формулам (12). 8. Проверить выполнение условия (19) с учетом того, что 9. Выполнить операцию усечения – xoa\xoas для xoas с tas min. 10. Изменить информационную структуру с учетом усечения шага 9, перейти к шагу 3. 11. Конец. Предлагаемый укрупненный алгоритм реализует метод, в основе которого с целью минимизации затрат формируется информационная структура ЛА. Список литературы 1. Бизяев Р.В. Системная технология диагностирования стендовых изделий РКТ. - М.: Изд-во МАИ, 1997. - 164 с. 2. Клир Дж. Системология. Автоматизация решения системных задач. / Пер. с англ. - М.: Радио и связь, 990. - 544 с. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=560 |
Версия для печати Выпуск в формате PDF (1.31Мб) |
| Статья опубликована в выпуске журнала № 4 за 2004 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Формирование программ развития больших систем административно-организационного управления
- Формулировка задачи планирования линейных и циклических участков кода
- Нейроподобная сеть для решения задачи оптимизации антенной решетки
- Знания в интеллектуальных системах
- Системы компьютерной поддержки процессов анализа, синтеза и планирования решений в условиях неопределенности
Назад, к списку статей



 (3)
(3)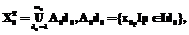 (4)
(4) (5)
(5)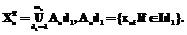 (6)
(6)
 .
. (8)
(8) (9)
(9) (10)
(10)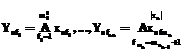 . (11)
. (11) где L0=m0+n0 – из (3) и (4); Ln=mn+nn – из (5) и (6);
где L0=m0+n0 – из (3) и (4); Ln=mn+nn – из (5) и (6); ,
,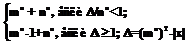 . (12)
. (12)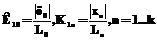 ,
, ,
, ,
, ,
,  ;
;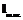 ;
; (16)
(16)
 .
.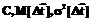 известны, то (16) перепишем в виде:
известны, то (16) перепишем в виде: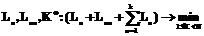 (17)
(17)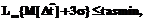 (18)
(18) (19)
(19) – длина линий связи между элементами выбранной на i-м шаге информационной структуры. При выполнении условия перейти к шагу 11, в противном случае – к шагу 1.
– длина линий связи между элементами выбранной на i-м шаге информационной структуры. При выполнении условия перейти к шагу 11, в противном случае – к шагу 1.