Авторитетность издания
Добавить в закладки
Следующий номер на сайте
К вопросу о наилучших раскладках английских и русских символов на компьютерной клавиатуре
Аннотация:
Abstract:
| Авторы: Усманов З.Д. (zafar-usmanov@rambler.ru) - Российско-Таджикский (Славянский) университет (профессор), Душанбе, Таджикистан, доктор физико-математических наук, Солиев О.М. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 22973 |
Версия для печати Выпуск в формате PDF (1.31Мб) |
Пусть
Пусть
В условиях (1), (2) на раскладке
работа, затрачиваемая на набор R-текста, достигает минимального значения*. Здесь сама раскладка представлена в виде подстановки n-й степени, указывающей, на каких клавишах размещаются те или иные символы. Согласно (3) наилучшей является такая раскладка, в которой чаще встречающиеся символы размещаются на менее трудоемких клавишах, а реже встречающиеся – на более трудоемких. И еще один вывод следует из (3): при проектировании оптимальной клавиатуры, сводящейся к привязке каждого символа к той или иной клавише, более важной является информация о характере ранжировки клавишей и символов, нежели точные числовые значения показателей В настоящей статье теоретическое решение проблемы адаптируется к практической ситуации, то есть к раскладке символов на русской и английской клавиатурах. В связи с тем, что дословное применение теоретического подхода в этих случаях реализовать не удается, мы говорим не об оптимальных, а о наилучших раскладках символов на компьютерной клавиатуре. Ранжировка клавишей. Для русского языка нас будет интересовать раскладка 33 букв русского алфавита, а для английского – 26 латинских букв, 3 знаков препинания (точки, запятой и точки с запятой) и знака апострофа. В обоих случаях предполагается, что переразмещение символов будет происходить в пределах тех клавишей, на которых они располагаются в настоящее время. Для ранжирования клавишей, основанного на значениях показателя Таблица 1
Здесь латинскими буквами и специальными символами указываются клавиши английской компьютерной клавиатуры, которые использованы для раскладки и которым снизу приписаны экспертные значения относительных трудозатрат на их активизацию. Отметим закономерность, исходящую от экспертов: клавишам, расположенным ближе к центру, выставлены меньшие оценки в сравнении с периферийными клавишами. В частности, легче достижимыми являются клавиши среднего ряда (на уровне Caps Lock), над которыми в исходном положении при слепом десятипальцевом методе печатания располагаются пальцы левой и правой рук. Таблица 1 определяет по существу ранжировку клавишей с точки зрения экспертов. К примеру, в качестве Частота встречаемости букв. Для изучения частот встречаемости букв были извлечены случайные выборки из литературных произведений, газетных и журнальных статей, причем из русских текстов объемом порядка 115 страниц, содержащих 281117 знаков, а из английских текстов – порядка 120 страниц с 294186 знаками. Путем обработки всевозрастающего количества страниц была выявлена экспериментальная сходимость относительных частот встречаемости букв. Методами корреляционного и дисперсионного анализов установлено, что случайные выборки как русских, так и английских текстов объемом не менее 10 страниц (приблизительно 24 000 знаков) являются репрезентативными (R-текстами) в том смысле, что они характеризуются статистически неразличимыми распределениями относительных частот встречаемости букв. В таблицах 2 (для русского языка) и 3 (для английского) указанные частоты (для соответствующих букв) приведены в порядке убывания их значений. Таблица 2
Таблица 3
Отметим, что в таблице 3 в сравнении с таблицей 2 помимо букв указаны также и частоты встречаемости 4-х знаков, которые принимают участие в раскладках на клавишах компьютерной клавиатуры. Инвариант ранжирования букв. Как следует из предыдущего пункта, распределение относительных частот является статистическим инвариантом по отношению к R-текстам. Однако для проектирования оптимальной раскладки символов требуется не этот результат, а сведения о ранжировке букв. Изучение этого вопроса показало, что ранжировка букв, порождаемая относительными частотами, оказывается неустойчивой (неинвариантной) по отношению к R-текстам. Иными словами, для R-текстов различных отраслей знания, различных авторов, различных произведений одного и того же автора и т.п. ранжировки букв оказываются различными. Такая ситуация не позволяет осуществить оптимальную раскладку букв по методу, описанному выше. По этой причине R-тексты были подвергнуты более детальному исследованию, в результате чего удалось обнаружить новый нетривиальный инвариант, характеризующий устойчивость ранжировки буквенных блоков. Дополнительный анализ распределения частот встречаемости символов в русских и английских R-текстах показал, что символы проявляют тенденцию группирования: для русского языка – в 17 блоков, в их числе 1 блок четырехбуквенный, 3 блока трехбуквенных, 7 двухбуквенных и 6 однобуквенных (табл. 4); а для английского языка – в 14 блоков, среди которых 1 блок пятибуквенный, 1 блок четырехбуквенный, 3 блока трехбуквенных, 3 двухбуквенных и 6 однобуквенных (табл. 5; удобства ради в этой таблице, а также в некоторых других местах статьи знаки препинания и апостроф названы буквами). В этих таблицах группы букв взяты в рамки, для однобуквенных блоков рамки не используются. Таблица 4
Таблица 5
Блочное группирование букв характеризуется следующими свойствами: · в пределах одного блока относительные частоты букв достаточно близки (отличаются в третьем или же в четвертом знаках после запятой); · блоки упорядочены в том смысле, что частоты встречаемости букв из одного блока превосходят частоты каждой буквы из последующих блоков; · ранжировки букв для различных R-текстов сохраняют неизменным порядок следования блоков; в пределах самих блоков входящие в них буквы равноправны и могут меняться местами. Таким образом, имеет место следующее статистическое утверждение: ранжировки буквенных блоков, представленные в таблицах 4 и 5, инвариантны по отношению к R-текстам. Экспериментальная проверка этого утверждения по отдельности для русского и английского языков выполнялась по следующей схеме. Вначале случайным образом производился выбор 8-10 R-текстов. Для каждой выборки вычислялись распределения относительных частот встречаемости букв. Затем буквам, входящим в один и тот же блок в согласии с таблицами 4 и 5, присваивались новые значения частот, равные их средним взвешенным значениям. Тем самым буквы становились равноправными в смысле ранжировки в пределах блока. Далее с учетом изменения частот блочных букв по откорректированным распределениям вновь осуществлялась ранжировка букв. При сравнении полученных ранжировок для различных R-текстов обнаружилось: · полное совпадение порядковых номеров одноблочных букв (так, русские буквы О, Е, С, Ч, Ф, Ю во всех ранжировках сохраняли свои порядковые номера 1, 2, 7, 22, 30, 33 соответственно); · полное совпадение порядка следования других блоков (так, трехбуквенный блок М-К-Д или же двухбуквенный блок Й-Ж во всех ранжировках привязывались соответственно к группам порядковых номеров 11-12-13 и 23-24). Дополнительные эксперименты подтверждали инвариантность блочного ранжирования. Оптимальная поблочная раскладка. Предыдущее утверждение предоставляет возможность получить оптимальную поблочную раскладку русских и английских букв на основе результата, описанного выше. Действительно, поскольку порядок букв внутри одного блока не имеет значения, естественно предположить, что их частоты равны. Присваивая относительным частотам этих букв одно и то же значение, равное средневзвешенному значению их прежних частот, мы получаем новое распределение относительных частот встречаемости букв в R-текстах. Это распределение, в свою очередь, порождает ранжировку букв (в порядке убывания их относительных частот), однако неединственную вследствие того, что буквы из одного блока не поддаются упорядочению. В таких предпосылках применение формулы (3) позволяет получить раскладку букв на компьютерной клавиатуре, которую естественно воспринимать как оптимальную раскладку буквенных блоков. Если порядковые номера, используемые в таблицах 4 и 5, интерпретировать в качестве номеров клавишей компьютерной клавиатуры, то сами таблицы по существу в развернутом виде характеризует формулу (3), то есть задают оптимальную поблочную раскладку букв (с произвольным порядком букв в самих блоках). Наилучшие раскладки. Оптимальная поблочная раскладка букв не приводит к окончательному результату. Причина в том, что она однозначным образом закрепляет группу букв за группой клавишей (например, русские буквы А и И – за клавишами Следующий этап в принятии решения естественно связать с поисками таких раскладок, которые наилучшим образом приспособлены к реализации слепого десятипальцевого метода работы на клавиатуре. В соответствии с этим методом клавиши клавиатуры разделяются на 8 зон. Каждая зона предназначается для работы конкретного пальца левой и правой руки. При использовании этого метода чрезвычайно неудобными считаются такие ситуации, когда приходится печатать подряд две буквы, расположенные в зоне работы одного и того же пальца. Вероятно, полностью устранить возникновение таких ситуаций невозможно, однако их число можно уменьшить за счет подходящей расстановки букв внутри буквенных блоков. Это, кстати, дает возможность определить однозначную раскладку букв по клавишам клавиатуры. Отметим, что на этапе окончательного формирования раскладок русских и английских букв на компьютерной клавиатуре существенно используются данные о частотах встречаемости в текстах пар букв. Получаемые таким образом раскладки названы нами наилучшими, поскольку на первом этапе их проектирования оптимальным образом размещаются буквенные блоки, а на втором фиксация позиций букв внутри блоков осуществляется для наилучшего обеспечения слепого десятипальцевого метода печатания. Необходимо отметить, что на втором этапе проектирования не удается полностью устранить элементы субъективизма в принятии решений, а потому в итоге наилучших раскладок может оказаться несколько. Далее приводится по одному из вариантов наилучших раскладок русских и английских букв на компьютерной клавиатуре. Таблица 6
Таблица 7
В таблицах 6 и 7 в верхней строке символы и буквы английской клавиатуры указывают позиции тех клавишей, на которых располагаются русские и английские буквы в соответствии с наилучшей раскладкой. Замечание. При оптимальной поблочной раскладке букв, а затем и наилучшем обеспечении слепого десятипальцевого метода печатания использовалась ранжировка клавишей, полученная на основе экспертных оценок. Однако мы могли бы воспользоваться и другой ранжировкой, например П. Клауслера, в которой группам клавишей присваиваются одинаковые весовые значения трудозатрат. Вполне понятно, что в этом случае после применения оптимальной поблочной раскладки букв нам пришлось бы иметь дело с большим разнообразием раскладок и осуществлять перебор большего числа вариантов размещения букв для наилучшего обеспечения слепого десятипальцевого метода печатания. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=566 |
Версия для печати Выпуск в формате PDF (1.31Мб) |
| Статья опубликована в выпуске журнала № 4 за 2004 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Системы компьютерной поддержки процессов анализа, синтеза и планирования решений в условиях неопределенности
- Знания в интеллектуальных системах
- Метод оценки безопасности информации в автоматизированных системах
- Инструментальные и программные средства построения сетевых моделей
- Потоковый анализ программ, управляемый знаниями
Назад, к списку статей



 – некоторая клавиатура, состоящая из
– некоторая клавиатура, состоящая из  клавишей
клавишей  , причем каждой клавише приписано положительное число
, причем каждой клавише приписано положительное число 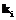 (
( ), указывающее на количество энергии, которую следует затратить для того, чтобы активизировать (нажать на)
), указывающее на количество энергии, которую следует затратить для того, чтобы активизировать (нажать на)  . Предполагается, что клавиши пронумерованы таким образом, что
. Предполагается, что клавиши пронумерованы таким образом, что . (1)
. (1) – конечный набор символов
– конечный набор символов 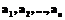 (буквы какого-либо естественного языка
(буквы какого-либо естественного языка  и, возможно, некоторые знаки препинания), предназначенный для раскладки на клавишах множества
и, возможно, некоторые знаки препинания), предназначенный для раскладки на клавишах множества 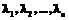 встречаемости этих символов в репрезентативных текстах (
встречаемости этих символов в репрезентативных текстах (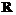 -текстах), написанных на языке
-текстах), написанных на языке  . (2)
. (2)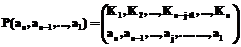 (3)
(3)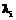 , на основе которых производятся сами ранжировки.
, на основе которых производятся сами ранжировки. следует рассматривать клавишу “~” английской клавиатуры, показатель которой
следует рассматривать клавишу “~” английской клавиатуры, показатель которой  имеет наибольшее значение; в качестве
имеет наибольшее значение; в качестве  – клавишу F, показателю которой приписывается наименьшее значение,
– клавишу F, показателю которой приписывается наименьшее значение,  и т.д.
и т.д.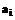
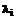
 ,
,  , а буквы Л, Р и В или же Ь, Г, Б и З – за клавишами
, а буквы Л, Р и В или же Ь, Г, Б и З – за клавишами  ,
,  ,
,  или
или  ,
, 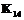 ,
,  и
и  соответственно), однако внутри группы (блока) клавишей порядок следования букв оставляет произвольным. Следовательно, оптимальная поблочная раскладка не дает единственного решения интересующей нас проблемы. Тем не менее, она в сравнении с начальной ситуацией, когда в нашем распоряжении имелось 33! » 1040 возможных раскладок на русской клавиатуре и 30! » 1032 – на английской, значительно сокращает число допустимых решений и предоставляет дальнейший выбор из 663552 оставшихся раскладок для русского языка и 4976640 раскладок для английского, которые возникают вследствие того, что внутри каждого из блоков возможны перестановки букв.
соответственно), однако внутри группы (блока) клавишей порядок следования букв оставляет произвольным. Следовательно, оптимальная поблочная раскладка не дает единственного решения интересующей нас проблемы. Тем не менее, она в сравнении с начальной ситуацией, когда в нашем распоряжении имелось 33! » 1040 возможных раскладок на русской клавиатуре и 30! » 1032 – на английской, значительно сокращает число допустимых решений и предоставляет дальнейший выбор из 663552 оставшихся раскладок для русского языка и 4976640 раскладок для английского, которые возникают вследствие того, что внутри каждого из блоков возможны перестановки букв.