Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Алгоритмы и процедуры построения билинейных моделей непрерывных производств
Аннотация:
Abstract:
| Авторы: Виноградов Г.П. (wgp272ng@mail.ru) - Тверской государственный технический университет (профессор), Тверь, Россия, доктор технических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 14537 |
Версия для печати Выпуск в формате PDF (1.36Мб) |
Линейные модели непрерывных производств в форме затраты–выпуск вида Известен ряд работ, в которых описываются алгоритмы оценки параметров моделей в форме затраты–выпуск с переменными параметрами. Наибольший интерес представляют: метод граничных ва- риантов, метод, разработанный М.С. Меттом и М.Н. Нуриевым [1], и метод диапазонных моде- лей [2,3]. Недостатком первых двух методов является отсутствие способа учета свойств области допустимых значений входных параметров, которая, как правило, для процессов химической технологии имеет сложную конфигурацию и является невыпуклой. Поэтому принцип оценки граничных значений изменения каждого параметра в отдельности приводит к тому, что, например, в случае нормального закона распределения вероятность правильного описания моделью реального процесса не будет превышать 0.68. Точность построения моделей будет ниже, если процесс характеризуется значительным запаздыванием момента выпуска продукции относительно факта использования сырья, а закон распределения входных и выходных переменных отличается от нормального. Недостатком третьего метода является зависимость размерности задачи оценивания параметров модели от величины выборки, так, для примера, приведенного в работе [2], для двух входов и выходов и числа наблюдений, равного 20, решение задачи линейного программирования для оценки параметров модели производилось для 76 переменных и 65 ограничений в форме равенств. Рекомендации, приведенные в [3] по уменьшению зависимости размерности решаемой задачи от выборки, носят эвристический характер и требуют предварительного анализа свойств процесса. Как правило, процессы химической технологии относятся к классу нестационарных процессов вследствие изменения активности катализатора, структуры технологического комплекса, состава сырья и ряда других возмущающих воздействий. Действие этих факторов приводит к тому, что текущее значение вектора X={xi, i= Общая постановка задачи имеет следующий вид. Пусть существует соотношение FÌХÄY. (1) Область изменения показателей качества Dy задана в виде Ymin. Область Dx имеет сложную конфигурацию и может быть невыпуклой, хотя в ряде случаев можно подобрать такое преобразование f(х), что область Df(х) будет выпуклой. Однако сложность области Dx вследствие функциональной взаимосвязи параметров X такова, что определение границ изменения расходных коэффициентов независимо друг от друга для различных входных материальных потоков возможно только в том случае, если область Dx аппроксимировать прямоугольным параллелепипедом, грани которого параллельны координатным плоскостям: B={X|Xj–X*|£DXj, j= где X* – номинальное значение j-го параметра; DXj – допуск в абсолютных величинах на j-й параметр, с помощью которого задаются пределы изменения параметров в области Dx, при которых обеспечивается выполнение VÎDy. Длина ребра параллелепипеда определяет диапазон изменения режимных параметров при заданных значениях входных материальных потоков и условии, что VÎDy. Таким образом, задача оценки параметров модели типовых технологических операций в форме затраты–выпуск может быть решена в два этапа. На первом этапе, исходя из требований к показателям качества, определяется диапазон изменения выходных параметров V. Область изменения режимных параметров и входных воздействий Dx аппроксимируется прямоугольным параллелепипедом, грани которого параллельны координатным плоскостям. На втором этапе для XjÎ aij = min aij = max i= где l – номер режимного параметра. Степень адекватности моделей с переменными параметрами будет определяться точностью аппроксимации области Dx брусом В и может быть оценена с помощью критериев, приведенных в работе [5]. Алгоритм 1. Пусть область изменения режимных параметров Dx определяется системой неравенств вида gi(Х)£bi, i= 1. Выберем Wt(Х) 2. Обозначим через X1={X11,…,X1i,….,X1m} и d = {d1,…,di,…,dm} координаты одной вершины бруса В и его линейные размеры соответственно. 3. Введем вектор F(X) W(X)³Wt gi(Х) £bi, i=
Применение для решения задачи (2) известных методов математического программирования ограничено тем, что с увеличением числа переменных X={Xi, i= Анализ результатов экспериментальных расчетов показал, что не все вершины вложенного бруса лежат на границе Dx. Следовательно, для сокращения размерности задачи целесообразно выделить вершины, лежащие на границе Dx, и организовать проверку принадлежности Dx только выделенных Xk, k= 4. Определим точку аÎDx такую, что W(a)= maxW(X)|gi(Х)£bi, i= W(Xl)³Wt, gi(Х)£bi, i= 5. В брусе В0 проводятся 2m-1 диагоналей и определяется точка их пересечения X=C. Начало координат переносится в точку C, делается замена переменных Z=X-C. Решается задача F(Z) W(Z)³ Wt , gi(Х) £bi, i= Zmin £ Z £ Zmax. 6. Для каждой из 2m найденных точек строится брус Вi, i= 7. Очевидно, что F(X) будет определяться выбранной точкой С. Будем варьировать координаты точки С методом случайного поиска. Для этого из точки Х=С производится k+1-й шаг в случайном направлении, определенном случайным единичным вектором gk. Величина шага задается параметром DCk. При Ck+DCk*gkÎDx определяется maxF(Xk+1, Ck+1). Если F(Xk+1, Ck+1)> F(Xk, Ck), то Ck+1=Ck+ DCk*gk, в противном случае вычисляется новый случайный вектор gk. Подобные шаги выполняются до тех пор, пока при серии из N шагов не будет увеличения целевой функции. Если при k³N увеличения целевой функции не наблюдается, то изменяется шаг DCk и производится расчет вектора Ck+1. В качестве критерия окончания поиска используется величина приращения вектора Ck и целевой функции F(Xk). Полученные допуски на режимные параметры используются для расчета коэффициентов модели подсистемы с переменными параметрами. Если aijmax < bijmax или aijmin > bijmin , то определяются новые значения Xmin и Xmax путем решения уравнений
8. Решение задачи (3) повторяется с новыми значениями ограничений на Xi, i= Предложенный подход позволяет существенно сократить число проверяемых вершин по сравнению с методами математического программирования. Оценка эффективности работы алгоритма на тестовых и реальных задачах показала его хорошую сходимость и точность поиска параметров модели. В ряде случаев хорошее решение было получено уже на первом шаге поиска. Зачастую получение математической модели подсистемы связано с большими затратами ресурсов. Поэтому целесообразно рассмотреть метод, который исключает использование функциональных зависимостей между выходами и входами, а непосредственно использует экспериментальную выборку. Алгоритм 2. Пусть область изменений технологических параметров охватывает область допустимых значений Dx, определенную технологическим регламентом. Пусть задано условие, определяющее пределы изменения критерия эффективности: Vmin£V£Vmax. Пусть соотношение между допусками задано в виде DX1b1 = DX2b2 = ... = DXmbm, где b1, b2, ... , bm – весовые коэффициенты, отражающие усредненное влияние технологических факторов на показатели качества, то есть bi = где bij – весовые коэффициенты, учитывающие влияние i-го фактора на j-й показатель качества. Выбор значения bij определяется спецификой решаемой задачи с учетом некоторой совокупности требований и может быть назначен экспертным путем; m – размер выборки. 1. Обозначим через Xni, i=
где Pk= n – число экспериментальных точек. 2. Для первого приближения выберем в качестве центра бруса среднеарифметическое число точек, для которых признак Pk=1: Sxi = Xij*= где ni – число экспериментальных точек, для которых Pk=1. 3. Проведем замену переменных Zni=bi(Xni*–Sni), i= |Z1| = |Z2| = … = |Zm|. (4) 4. Раскрывая знаки абсолютных значений в (4), получим уравнения, различающиеся комбинацией знаков при Zi. Общее число таких уравнений, а значит, и диагональных прямых, не лежащих в гиперплоскостях граней m-мерного гиперкуба, равно 2m-1. Точки Cr, r= 5. В качестве Zr выберем точку пересечения диагональных прямых с гиперплоскостями опи- санного куба B0 (алгоритм построения приведен выше): Zi=ai и Zr=bi, где ai=maxZij; bi=minZij, i= 6. Координаты точек Gr находим последовательным делением отрезков Sz, Zr пополам, определяя каждый раз, какой области (Dz или Ur(h) = {Ur1(h), Ur2(h), …, Urm(h)}, Wr(h) = {Wr1(h), Wr2(h), …, Wrm(h)}, где h – номер последовательного деления. Таким образом, процедура деления отрезков начинается при Ur(1)=Sz и Wr(h)=Zr , r= Середина отрезка Ur(h) и Wr(h) 'на h-м шаге имеет координаты Cr(h)= Для каждого последующего шага процедуры производится коррекция координат вершин отрезков следующим образом: Ur(h+1)= Wr(h+1)= Процедура заканчивается при достижении заданной точности, то есть при выполнении условия: D(Ur(h) , Wr(h))£e, r= В результате имеем Сr = Сr(h+1). Вершины куба допусков с центром в точке Sz имеют координаты Zrкуба =C*gr, r= C*=|Cri| для любого i определяются из условия вписания куба в Dz, то есть у куба с центром в начале координат абсолютные значения координат любой вершины одинаковы. 7. Нахождение оптимального положения центра куба допусков является задачей нелинейного программирования без ограничений с критерием C* ®max, (5) C* = f(Sz). (6) 8. Искомые допуски определяются с учетом проведенных ранее преобразований координат по формулам: Ximin = где Szi* – оптимальные, в смысле (5) значения координат центра допусков. Так как зависимость (6) неизвестна, то определение Szi осуществляется поисковым алгоритмом, не использующим производные, в данном случае алгоритмом Хука-Дживса. Модель в форме расходных коэффициентов с использованием полученных результатов ищется по методике, описанной выше. Необходимость периодической коррекции моделей подсистемы вызвана нестационарным характером рассматриваемой ХТС вследствие: - высокой агрессивности используемого сырья и полупродуктов; - изменения свойств катализатора при отравлении каталитическими ядами; - варьирования входной нагрузки по сырью и энергоресурсам. При этом каждое новое наблюдение должно использоваться для коррекции ранее полученного результата. Если область допустимой вариации параметров Dz представить как пересечение гиперповерхности Yi = Fi(X) (7) с гиперповерхностью заданного качества |Fi(X)|= = emin, то действие описанных выше дестабилизирующих факторов приводит к изменению вида уравнения (7) и, следовательно, области Dx. Поэтому возникают задачи: - определения в новой ситуации допустимых пределов изменения по каждому параметру в отдельности; - перераспределения допусков на параметры с целью достижения заданных требований к качеству функционирования системы и ее элементов. В качестве критерия функционирования технологического агрегата можно рассматривать вероятность нахождения выходной величины Y в заданном поле допуска при фиксированных значениях входных переменных Хi, i= P{VÎ[A,B]|Xi} > P0, (8) где Р0 – заданная вероятность, величина которой больше, например, 0,7. Тогда задача коррекции допусков сводится к отысканию в моменты времени ti такой области Dz, чтобы XÎDx = Пусть P(V(Xi)) – плотность распределения выходных параметров технологического агрегата. Тогда при выполнении предположения о нормальном законе распределения можно записать условие (8) в следующем виде:
= Таким образом, задача коррекции параметров модели комплексов с переменными параметрами сводится к коррекции моделей отдельных агрегатов типа f(X1, X2, …, Xm), решению уравнения (8) и к последующей аппроксимации полученной области гиперпараллелепипедом. Список литературы 1. Метт М.С., Нуриев М.Н. К вопросу определения параметров моделей текущего планирования нефтеперерабатывающего предприятия. // Изв. вузов. Нефть и газ. - 1975. - №4. - С. 88-92. 2. Зенков В.В., Соркин Л.Р. Построение и использование диапазонных моделей. // УСИМ. - 1978. - №4. - С.216-221. 3. Зенков В.В. Диапазонные модели участков производства для АСУП. // Изв. АН СССР: Техническая кибернетика. - 1975. - №5. - С.57-63. 4. Виноградов Г.П., Кузнецов В.Н., Торбин С.И. Алгоритм многоуровневой оптимизации производственного комплекса с переменными параметрами. // Матер. 3-й Всесоюзн. конф.: Математические методы в химии. Т.4. Оптимизация. - М.: ЦНИИТЭИнефтехим. - 1980. - С.13-19. 5. Абрамов О.В., Бернацкий Ф.И., Здор В.В. Параметрическая коррекция систем управления. - М.: Энергоиздат, 1982. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=642 |
Версия для печати Выпуск в формате PDF (1.36Мб) |
| Статья опубликована в выпуске журнала № 2 за 2003 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Формирование программ развития больших систем административно-организационного управления
- Компьютер - хранитель домашнего очага
- Структурно-параметрическая идентификация функций занятости и прогнозирование спроса на молодых специалистов
- Статическая обработка спецификаций программных систем реального времени
- Функционально-информационные модели бухгалтерского учета
Назад, к списку статей



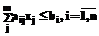 , где aijÎDa, называются билинейными. Коэффициенты aij в них являются переменными параметрами и зависят от режимных параметров, таких как температура, давление и т.п. При решении задач оптимизации по таким моделям необходимо определять и вектор X*, и оптимальные значения расходных норм a*ij.
, где aijÎDa, называются билинейными. Коэффициенты aij в них являются переменными параметрами и зависят от режимных параметров, таких как температура, давление и т.п. При решении задач оптимизации по таким моделям необходимо определять и вектор X*, и оптимальные значения расходных норм a*ij.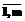 } входных материальных потоков и режимных параметров, а также вектора Y=(yj,
} входных материальных потоков и режимных параметров, а также вектора Y=(yj, ) – показателей свойств выходного продукта и технико-экономических показателей – изменяется в некоторой области Dx и Dy соответственно. Это позволяет предложить ряд простых процедур построения билинейных моделей, основанных на вписывании в область изменения режимных параметров гиперпараллелепипеда [4].
) – показателей свойств выходного продукта и технико-экономических показателей – изменяется в некоторой области Dx и Dy соответственно. Это позволяет предложить ряд простых процедур построения билинейных моделей, основанных на вписывании в область изменения режимных параметров гиперпараллелепипеда [4]. ÛVÎDy,
ÛVÎDy, , l=
, l=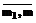 , при которых будет выполняться
, при которых будет выполняться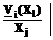 min XjÎ
min XjÎ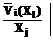 max XjÎ
max XjÎ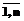 ; j=
; j=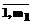 ,
, . Предположим, что W(X) – вогнутая функция, а gi(Х) – выпуклые функции и на множестве Dx, определяемом системой неравенств gi(Х)£bi, i=
. Предположим, что W(X) – вогнутая функция, а gi(Х) – выпуклые функции и на множестве Dx, определяемом системой неравенств gi(Х)£bi, i=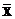 ={X1, X2, … ,X2m} координат вершин вложения бруса В. Задачу определения параметров модели с переменными параметрами сформулируем следующим образом:
={X1, X2, … ,X2m} координат вершин вложения бруса В. Задачу определения параметров модели с переменными параметрами сформулируем следующим образом: max
max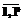 , X1min £X1 £ X1max (2)
, X1min £X1 £ X1max (2)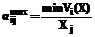 Xj ÎDx £ bijmin, j=
Xj ÎDx £ bijmin, j=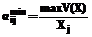 Xj ÎDx £ bijmax, i=
Xj ÎDx £ bijmax, i= .
. вершин.
вершин. max
max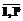 , (3)
, (3)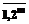 . Построение бруса осуществляется следующим образом. Из i-й точки на границе области B проводятся лучи параллельно координатным осям. Пересечение этих лучей с областью Dx определит mi вершин бруса Вi. Из mi новых вершин проводятся лучи, параллельные координатным плоскостям, и ищутся точки пересечений их между собой и областью Dx. Эта процедура повторяется до тех пор, пока не будут найдены 2m вершин бруса Bi. Для найденных 2m-(m+1) вершин проверяется условие принадлежности области Dx. Если вершина не принадлежит Dx, то производится корректировка линейных размеров бруса, для чего координаты этих вершин смещаются по диагонали, проведенной из лежащей вне области Dx вершины. Для 2m брусов Вi рассчитывается критерий Fl(X) и выбирается такое решение, которое соответствует max Fl(X).
. Построение бруса осуществляется следующим образом. Из i-й точки на границе области B проводятся лучи параллельно координатным осям. Пересечение этих лучей с областью Dx определит mi вершин бруса Вi. Из mi новых вершин проводятся лучи, параллельные координатным плоскостям, и ищутся точки пересечений их между собой и областью Dx. Эта процедура повторяется до тех пор, пока не будут найдены 2m вершин бруса Bi. Для найденных 2m-(m+1) вершин проверяется условие принадлежности области Dx. Если вершина не принадлежит Dx, то производится корректировка линейных размеров бруса, для чего координаты этих вершин смещаются по диагонали, проведенной из лежащей вне области Dx вершины. Для 2m брусов Вi рассчитывается критерий Fl(X) и выбирается такое решение, которое соответствует max Fl(X). .
. .
.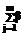 ij /m, i=
ij /m, i= ,
,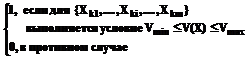 ;
;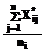 ;
;
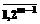 являются пересечением прямых, так как Sz = {Sz1, Sz2, …, Szm}ÎDz и существует Z2= {Z21, S22, …, S2m}ÎDz.
являются пересечением прямых, так как Sz = {Sz1, Sz2, …, Szm}ÎDz и существует Z2= {Z21, S22, …, S2m}ÎDz. .
.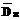 ) принадлежит полученная середина. Обозначим текущие границы отрезка, соединяющего Gs:
) принадлежит полученная середина. Обозначим текущие границы отрезка, соединяющего Gs: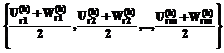 .
.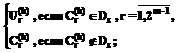

 , где gr – диагональная матрица отражения размера m´m, элементы которой равны: diag gr = {±1, ±1, …, ±1}.
, где gr – диагональная матрица отражения размера m´m, элементы которой равны: diag gr = {±1, ±1, …, ±1}.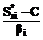 , Ximax =
, Ximax =  ,
,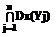 и выполнялось условие (8).
и выполнялось условие (8).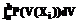 =
=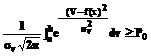 . (9)
. (9)