Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Прогнозирование на основе растущих пирамидальных сетей
Аннотация:
Abstract:
| Авторы: Гладун В.П. () - , Ващенко Н.Д. () - , Величко В.Ю. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 23109 |
Версия для печати Выпуск в формате PDF (1.13Мб) |
Прогнозированием, или предсказанием, называется деятельность, целью которой является определение таких характеристик объекта исследования или событий в его развитии, которые могут возникнуть в будущем или при выполнении определенных условий. Прогнозирование возможно, если известна зависимость прогнозируемой величины от условия, при выполнении которого должен осуществиться прогноз. В качестве условия прогнозирования может быть задан момент или интервал времени или определенная ситуация, которая в общем случае описывается набором значений и отношений некоторых величин или представляется примерами-прецедентами. Зависимость прогнозируемой величины от условия прогнозирования может быть представлена функцией, в частности функцией регрессии, если исследуются случайные процессы. В целях прогнозирования применяют методы экстраполирования функции, позволяющие определить ее значение при выполнении условия прогнозирования. Если условием является ситуация, нужно уметь распознавать ситуации этого класса или ситуации, им предшествующие. Итак, в зависимости от характера условия прогнозирования задачи прогнозирования сводятся к двум методическим стратегиям: экстраполирование функциональной зависимости или распознавание ситуаций. В статье рассматриваются методы прогнозирования, в основе которых лежит распознавание ситуаций. К задачам этого типа относятся, например, задачи предсказания существования химических соединений и материалов на основе анализа признаков, характеризующих составляющие элементы; прогнозирование поломок технических агрегатов путем анализа совокупности показаний датчиков, характеризующих их состояние; прогнозирование полезных ископаемых, природных и техногенных катастроф; медицинское прогнозирование и т.п. Распознавание ситуаций может быть выполнено на основе знания обобщенной закономерности, определяющей класс ситуаций, или путем сопоставления распознаваемых ситуаций с описаниями ситуаций-прецедентов, образующих некоторую обучающую выборку [1-3]. В первом случае обычно приходится строить логическое описание закономерности методами индуктивного вывода (проблема в современной терминологии получила название knowledge discovery – “обнаружение знаний”). Метод прецедентов по сути является реализацией вывода по аналогии. Мы рассмотрим и сравним оба принципа распознавания ситуаций в целях прогнозирования. В обоих случаях обрабатываемые данные представляют собой атрибутивные (признаковые) описания объектов или ситуаций. В методах, описанных далее, используются номинальные признаки, в связи с чем признаки, заданные на числовых шкалах, обрабатываются специальной процедурой, преобразующей числовые шкалы в номинальные. Для решения названных ранее задач используются признаки, характеризующие состав и физико-химические свойства материалов, элементы формы кривых, характеризующие состояние агрегатов, симптомы болезней и т.п. В статье излагаются теоретические и методологические положения, которые возникли в результате обобщения многочисленных экспериментальных исследований. Авторы выражают благодарность отечественным и зарубежным коллегам Н.Н.Киселевой, Й.Пао, С.ЛеКлэру, Ю.Г.Ткаченко за сотрудничество при выполнении исследований в области химии и материаловедения. Растущие пирамидальные сети При разработке современных компьютерных систем часто выдвигаются следующие требования: 1) не использовать “жесткие”, сложные для перестройки модели окружающей среды, поскольку реальные задачи решаются, как правило, в динамической, часто изменяющейся среде; 2) обеспечивать высокую ассоциативность компьютерного представления среды, в которой решаются задачи, с целью максимального снижения объема поисковых операций. Недостаточная ассоциативность компьютерного представления данных приводит к резкому увеличению сложности операций выбора с ростом объемов данных при использовании известных средств интеллектуального анализа данных, например, деревьев решений, грубых множеств, эволюционных ме- тодов [4,5]. С начала семидесятых годов выполнен ряд теоретических и прикладных исследований, нацеленных на решение аналитических проблем на основе методов, использующих организацию данных в виде растущих пирамидальных сетей [6-9], которая дает возможность обрабатывать большие объемы данных без введения каких-либо ограничений на сложность распределения анализируемых объектов в пространстве признаков. Пирамидальной сетью называется ациклический ориентированный граф, в котором нет вершин, имеющих одну заходящую дугу. Вершины, не имеющие заходящих дуг, называются рецепторами, остальные – концепторами. Подграф пирамидальной сети, включающий вершину a и все вершины, от которых имеются пути к вершине a, называется пирамидой вершины a. Вершины, входящие в пирамиду вершины a, образуют ее субмножество. Множество вершин, к которым имеются пути от вершины a, называется ее супермножеством. При построении сети входной информацией служат наборы значений признаков, описывающих некоторые объекты (материалы, состояния агрегата, ситуации, болезни и т.п.). На рисунке показана растущая пирамидальная сеть, построенная на основе обучающей выборки, в которой объектами являются пары химических элементов, образующих и не образующих двойные фтористые соединения. В таблице приведены описания объектов, где 1O, 1A, 1R, 1I – имена признаков, описывающих первый элемент соединения; 2O, 2A, 2R, 2I – имена признаков, описы Рецепторы соответствуют значениям признаков. В различных задачах это могут быть имена свойств, отношений, состояний, действий, объектов или классов объектов. Концепторы соответствуют описаниям объектов и их пересечениям. В начальном состоянии сеть состоит только из рецепторов. Концепторы формируются в результате работы алгоритма построения сети, который описан во многих публикациях [6-9]. Пирамидальные сети удобны для выполнения различных операций ассоциативного поиска. Например, можно выбрать все объекты, включающие заданное сочетание значений признаков, прослеживая пути, исходящие из вершины сети, которая соответствует этому сочетанию. Для выборки всех объектов, описания которых пересекаются с описанием заданного объекта, достаточно проследить пути, исходящие из вершин, образующих его пирамиду. Алгоритм построения сети обеспечивает автоматическое установление ассоциативной близости между объектами по общим элементам их описаний. Все процессы, связанные с построением сети, при обработке одного описания локализуются в относительно небольшой части сети – пирамиде, соответствующей этому описанию. Важным свойством пирамидальных сетей является их иерархичность, позволяющая естественным образом отображать структуру составных объектов и родовидовые связи. Концепторы сети соответствуют сочетаниям значений признаков, определяющих конъюнктивные классы объектов. Таким образом, при построении сети осуществляется классификация объектов. В пирамидальной сети информация хранится путем ее отображения в структуре сети. Информация об объектах и классах объектов представлена ансамблями вершин (пирамидами), распределенными по всей сети. Внесение новой информации вызывает перераспределение связей между вершинами сети, то есть изменение ее структуры.
Методы, использующие индуктивный вывод При использовании методов, включающих индуктивный вывод, аналитические проблемы решаются на основе обобщенных многопараметрических моделей классов объектов, которые формируются путем анализа обучающей выборки и затем представляются в виде логических выражений. В логике обобщенные многопараметрические модели классов объектов называются понятиями. Понятия интегрируют знания, необходимые для классификации, диагностики и прогнозирования. Задача индуктивного формирования понятий формулируется следующим образом. Пусть L – обучающая выборка, включающая объекты классов V1, V2,...,Vn, причем LÇVi¹Æ (i=1,2,...,n). Все объекты множества L заданы признаковыми описаниями. Каждый объект lÎL снабжен указанием типа lÎVi. Необходимо сформировать понятия Q1, Q2,...,Qn, которые соответствуют классам V1, V2,...,Vn и обеспечивают правильное распознавание объектов обучающей выборки L. Пусть имеется пирамидальная сеть, представляющая все объекты обучающей выборки L. Для формирования понятий Q1,Q2,...,Qn, соответствующих классам V1,V2,...,Vn, последовательно просматриваются пирамиды всех объектов обучающей выборки. При просмотре пирамид в сети выделяются специальные вершины, с помощью которых должно осуществляться распознавание объектов из объема понятия. Они называются контрольными вершинами данного понятия. При выборе контрольных вершин используются две характеристики вершин сети: {m1, m2,…, mn}, где mi (i=1,2,…,n) – число объектов класса Vi, в пирамиды которых входит данная вершина; и k – число рецепторов в пирамиде, соответствующей этой вершине (для рецепторов k=1). Алгоритмы формирования понятий в растущих пирамидальных сетях описаны в [6-9]. В сети, изображенной на рисунке, контрольные вершины $7, $3 и Na2BeF4 характеризуют класс А (пары элементов, образующих двойное фтористое соединение), контрольные вершины $4, $13 и NaF-ZnF характеризуют класс В (пары элементов, не образующих соединение). Сформированное понятие представляется в сети ансамблем контрольных вершин. На основе анализа сети специальная процедура строит понятие в форме логического выражения [8]. После того как понятие для некоторого класса объектов сформировано, проблема прогнозирования сводится к проблеме классификации описания прогнозируемого объекта (состояния, ситуации, процесса, события). Классификация новых объектов выполняется путем сравнения их признаковых описаний с понятием, определяющим класс прогнозируемых объектов [8]. Объекты можно классифицировать, вычисляя значение логических выражений, которые представляют соответствующие понятия. Переменным, соответствующим значениям признаков, которые встречаются в описании распознаваемого объекта, присваивается значение 1, остальным переменным – значение 0. Единичное значение всего выражения означает, что объект принадлежит классу, описываемому логическим выражением. Доказано, что время выполнения алгоритма формирования понятий всегда конечно. После выполнения алгоритма правило классификации полностью разделяет обучающую выборку на подмножества LÇVi¹Æ (i=1,2,...,n). Каждой вершине сети, имеющей k рецепторов в своем субмножестве, в s-мерном признаковом пространстве соответствует (s–k)-мерная плоскость. Плоскость содержит все точки, представляющие объекты, при восприятии которых возбуждается эта вершина; (s–k)-мерные плоскости, соответствующие контрольным вершинам понятия Qi, называются зонами понятия Qi. В результате работы алгоритма для каждого из формируемых понятий строится область из зон признакового пространства, содержащая все точки, представляющие те объекты обучающей выборки, которые входят в объем понятия, и не содержащая ни одной из точек, представляющих другие объекты обучающей выборки. Эта область аппроксимирует область распределения объектов из объема понятия. Поскольку аппроксимирующая область состоит из линейных элементарных областей (гипер- плоскостей), ограничивающая ее поверхность является кусочно-линейной. Следовательно, алгоритм осуществляет кусочно-линейное разделение объектов, входящих в объемы различных понятий. Понятия являются многопараметрическими моделями классов объектов. Важной особенностью метода формирования понятий в пирамидальных сетях является возможность включения в понятия исключающих признаков, не принадлежащих объектам исследуемого класса. В результате формируемые понятия имеют более компактную логическую структуру, что позволяет повышать точность диагноза или прогноза. В логическом выражении исключающие признаки представлены переменными с отрицаниями. Все поисковые операции ограничиваются сравнительно малым участком сети, который включает пирамиду объекта и вершины, непосредственно связанные с ней. В результате появляется прин- ципиальная возможность решать практические аналитические проблемы на основе больших объемов данных. Существует аналогия между основными процессами, имеющими место в растущих пирамидальных и нейронных сетях. Решающим преимуществом растущей пирамидальной сети является тот факт, что ее структура формируется полностью автоматически в зависимости от вводимых данных. В результате достигается оптимизация представления информации за счет адаптации структуры сети к структурным особенностям данных. Причем, в отличие от нейронных сетей, эффект адаптации достигается без введения априорной избыточности сети. Процесс обучения не зависит от предопределенной конфигурации сети. Недостатком нейронных сетей по сравнению с растущими пирамидальными сетями является также то, что выделенные в них обобщенные знания не могут быть явно представлены в виде правил или понятий. Это затрудняет их интерпретацию и понимание человеком. Методы, основанные на выводе по аналогии Вывод по аналогии является основой методов, суть которых состоит в анализе объектов обучающей выборки, наиболее “похожих” на исследуемый объект. Исследуемый объект считается принадлежащим классу, объекты которого представлены в пространстве признаков точками, расположенными наиболее близко к точке, представляющей исследуемый объект (метод К ближайших соседей). Проблема поиска аналогии должна решаться вместе с вопросами организации памяти, обеспечивающей установление аналогии объектов. В свете современных воззрений это должна быть память коннекционистского типа, допускающая параллельное выполнение поисковых операций и отражающая в своей структуре семантические пересечения блоков информации. Этим требованиям отвечают растущие пирамидальные сети. Алгоритм построения сети, работающий при вводе описаний новых объектов, одновременно является алгоритмом поиска в сети аналогов нового объекта, имеющих общие с ним фрагменты описаний. Степень подобия объектов оценивается мощностью пересечения их атрибутивных описаний. Эксперименты и применение Программный комплекс, используемый для проведения экспериментов и решения прикладных задач, включает три системы: - CONFOR, реализующую индуктивные методы; - ANALOGY, использующую вывод по аналогии; - DISCRET, с помощью которой признаки, заданные в числовых шкалах, преобразуются в номинальные. Эта задача называется задачей дискретизации. Дискретизация выполняется на шкалах числовых признаков путем сравнения распределений объектов обучающей выборки, принадлежащих различным классам. Комплекс прошел длительное испытание временем. Типичными прикладными задачами, для решения которых использовался комплекс, являются: прогнозирование новых химических соединений и материалов с заданными свойствами, прогнозирование в генетике, геологии, прогнозирование солнечной активности, медицинская и техническая диагностика, прогнозирование нарушений в работе сложных агрегатов [6,10]. Сравнение методов прогнозирования на основе индуктивного вывода и вывода по аналогии проводилось на задачах прогнозирования существования неорганических соединений с заданными свойствами. В качестве обучающей выборки использовались таблицы, содержащие атрибутивные описания двойных, тройных и четверных систем химических элементов, образующих и не образующих химические соединения. Обучающие выборки для двойных, тройных и четверных систем включали соответственно 1333, 4278 и 4963 описания, а экзаменационные выборки – 692, 2156 и 2536 описаний. Каждый химический элемент описывался 87 признаками. Описания двойных, тройных и четверных систем состояли соответственно из 174, 261 и 348 признаков. Была достигнута достаточно высокая точность прогноза – от 97,88% до 99,86%. На основании результатов экспериментов можно сделать следующие выводы. 1. Методы, основанные на аналогии с предварительным переводом числовых признаков в номинальные (система DISCRET), более просты в использовании и дают хорошие результаты прогноза при условии использования представительных обучающих выборок в случаях, когда области распределения объектов разных классов в пространстве признаков компактны. Без предварительного перевода признаков в номинальные реализация методов существенно усложняется из-за необходимости согласования единиц измерения для признаков, заданных в различных шкалах. 2. В методах, основанных на аналогии, результаты классификации зависят от параметра, определяющего размеры анализируемого окружения точки, представляющей объект в признаковом пространстве (например, число К в методе К ближайших соседей). Естественно выбирать К таким образом, чтобы обеспечить наилучшую классификацию объектов экзаменационной выборки. В этом случае параметр К может идеально разделять экзаменационную выборку и тем не менее давать плохие результаты при классификации других объектов. 3. Использование методов, включающих индуктивный вывод, снижает требования к обучающей выборке. Однако, в отличие от методов, основанных на аналогии, индуктивные методы гораздо чаще приводят к появлению неопределенного прогноза (ответа типа “не знаю”). Это происходит, в частности, в случаях, когда исследуемый объект одновременно соответствует закономерностям, характеризующим различные классы. Работу системы CONFOR, реализующей методы, включающие индуктивный вывод, можно сравнить с поведением серьезного исследователя, не бросающего слов на ветер. Работая в очень сложном “зашумленном” признаковом пространстве, он часто отвечает “не знаю”, однако дает прогноз с большой степенью точности. 4. Иногда важным достоинством индуктивных методов прогнозирования является создание обобщенной модели исследуемого класса объектов, которая представляется в виде логического выражения, удобного для интерпретации человеком. Исследования, выполненные на сложных данных большого объема, показали высокую эффективность применения растущих пирамидальных сетей для решения аналитических задач. Такие качества, как простота внесения изменений, совмещение процессов ввода информации с ее классификацией, обобщением и выделением существенных признаков, высокая ассоциативность, делают растущие пирамидальные сети важной компонентой прогнозирующих систем. Выводы, приведенные ранее, позволяют правильно выбрать метод анализа в зависимости от условий исследования. Список литературы 1. Загоруйко Н.Г. Прикладные методы анализа данных и знаний. -Новосибирск: Изд-во ин-та математики, 1999.- 270 с. 2. Журавлев Ю.И., Рязанов В.В. Об извлечении знаний из выборок прецедентов в моделях классификации, основанных на принципе частичной прецедентности. //Тр. междунар. науч.-практ. конф.: KDS-2001: Знание-Диалог-Решение. - СПб. - 2001. - С. 232 – 237. 3. Закревский А.Д. Логика распознавания. –Минск: Наука и техника, 1988. - 118 с. 4. Quinlan R. “Induction of decision trees”. Machine Learning 1, 1986, pp.81-106. 5. Piatetsky-Shapiro G.and Frawley W.J., editors. Knowledge Discovery in Databases. AAAI Press, Menlo Park, California, 1991. 6. Гладун В.П. Партнерство с компьютером. Человеко-машинные целеустремленные системы. – Киев: Port-Royal, 2000.- 128 с. 7. Gladun V.P., Rabinovich Z.L. “Formation of the World Model in Artificial Intelligence Systems”. In: Machine Intelligence, 9, Ellis Herwood Ltd., Chichester, 1980, pp. 299-309. 8. Гладун В.П. Планирование решений. –Киев: Наукова думка, 1987. –168 с. 9. Gladun V.P. and Vashchenko N.D. “Analytical processes in pyramidal networks”. International journal on information theories & applications. FOI-COMMERCE, Sofia, Vol. 7, №3 - 2000, pp. 103-109. 10.Kiselyova N., Gladun V., Vashchenko N.. “Computational Materials Design Using Artificial Intelligence Methods”. Journal of Alloys and Compounds. 279(1998), pp. 8-13. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=702 |
Версия для печати Выпуск в формате PDF (1.13Мб) |
| Статья опубликована в выпуске журнала № 2 за 2002 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Компьютерная технология проектирования перестраиваемых нерекурсивных фильтров
- Компьютер - хранитель домашнего очага
- Учебно-исследовательский программно-лабораторный комплекс NET_LAB
- Системы баз данных и знаний, разработанные в Республике Куба
- Компьютерный тренажер для операторов технологических процессов доменного производства
Назад, к списку статей



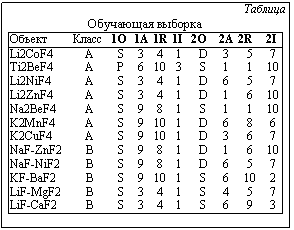 вающих второй элемент соединения; буквы и цифры в ячейках – значения соответствующих признаков.
вающих второй элемент соединения; буквы и цифры в ячейках – значения соответствующих признаков.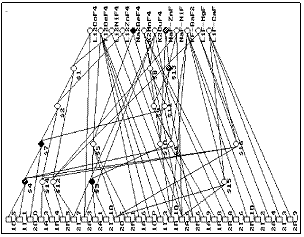 Конечно, в полной мере достоинства пирамидальных сетей проявляются при их физической реализации, допускающей параллельное распространение сигналов по сети. Важным свойством сети как средства хранения информации является то, что возможность параллельного распространения сигналов сочетается в ней с возможностью параллельного приема сигналов на рецепторы.
Конечно, в полной мере достоинства пирамидальных сетей проявляются при их физической реализации, допускающей параллельное распространение сигналов по сети. Важным свойством сети как средства хранения информации является то, что возможность параллельного распространения сигналов сочетается в ней с возможностью параллельного приема сигналов на рецепторы.